|
Zahlen
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zahlen
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country"). Numbers used for counting are called ''Cardinal number, cardinal numbers'', and numbers used for ordering are called ''Ordinal number, ordinal numbers''. Natural numbers are sometimes used as labels, known as ''nominal numbers'', having none of the properties of numbers in a mathematical sense (e.g. sports Number (sports), jersey numbers). Some definitions, including the standard ISO/IEC 80000, ISO 80000-2, begin the natural numbers with , corresponding to the non-negative integers , whereas others start with , corresponding to the positive integers Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). The natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Number Theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic objects such as algebraic number fields and their rings of integers, finite fields, and Algebraic function field, function fields. These properties, such as whether a ring (mathematics), ring admits unique factorization, the behavior of ideal (ring theory), ideals, and the Galois groups of field (mathematics), fields, can resolve questions of primary importance in number theory, like the existence of solutions to Diophantine equations. History of algebraic number theory Diophantus The beginnings of algebraic number theory can be traced to Diophantine equations, named after the 3rd-century Alexandrian mathematician, Diophantus, who studied them and developed methods for the solution of some kinds of Diophantine equations. A typical Diophantin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can be represented by symbols, called ''numerals''; for example, "5" is a numeral that represents the number five. As only a relatively small number of symbols can be memorized, basic numerals are commonly organized in a numeral system, which is an organized way to represent any number. The most common numeral system is the Hindu–Arabic numeral system, which allows for the representation of any number using a combination of ten fundamental numeric symbols, called digits. In addition to their use in counting and measuring, numerals are often used for labels (as with telephone numbers), for ordering (as with serial numbers), and for codes (as with ISBNs). In common usage, a ''numeral'' is not clearly distinguished from the ''number'' th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blackboard Bold
Blackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol (usually vertical or near-vertical lines) are doubled. The symbols usually denote number sets. One way of producing blackboard bold is to double-strike a character with a small offset on a typewriter. Thus, they are also referred to as double struck. In typography, such a font with characters that are not solid is called an "inline", "shaded", or "tooled" font. History Origin In some texts, these symbols are simply shown in bold type. Blackboard bold in fact originated from the attempt to write bold letters on blackboards in a way that clearly differentiated them from non-bold letters (by using the edge rather than the point of a chalk). It then made its way back into print form as a separate style from ordinary bold, possibly starting with the original 1965 edition of Gunning and Rossi's textbook on complex analysis. Use in textbooks In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixed Number
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A ''common'', ''vulgar'', or ''simple'' fraction (examples: \tfrac and \tfrac) consists of a numerator, displayed above a line (or before a slash like ), and a non-zero denominator, displayed below (or after) that line. Numerators and denominators are also used in fractions that are not ''common'', including compound fractions, complex fractions, and mixed numerals. In positive common fractions, the numerator and denominator are natural numbers. The numerator represents a number of equal parts, and the denominator indicates how many of those parts make up a unit or a whole. The denominator cannot be zero, because zero parts can never make up a whole. For example, in the fraction , the numerator 3 indicates that the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy and music theory. Euler is held to be one of the greatest mathematicians in history and the greatest of the 18th century. A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss remarked: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." Euler is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elements Of Algebra
''Elements of Algebra'' is an elementary mathematics textbook written by mathematician Leonhard Euler around 1765 in German. It was first published in Russian as "''Universal Arithmetic''" (''Универсальная арифметика''), two volumes appearing in 1768-9 and in 1770 was printed from the original text. ''Elements of Algebra'' is one of the earliest books to set out algebra in the modern form we would recognize today (another early book being ''Elements of Algebra'' by Nicholas Saunderson, published in 1740), and is one of Euler's few writings, along with ''Letters to a German Princess'', that are accessible to the general public. Written in numbered paragraphs as was common practice till the 19th century, ''Elements'' begins with the definition of mathematics and builds on the fundamental operations of arithmetic and number systems, and gradually moves towards more abstract topics. In 1771, Joseph-Louis Lagrange published an addendum titled ''Additions to Euler ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entier
In mathematics and computer science, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or . For example, , , , and . Historically, the floor of has been–and still is–called the integral part or integer part of , often denoted (as well as a variety of other notations). Some authors may define the integral part as if is nonnegative, and otherwise: for example, and . The operation of truncation generalizes this to a specified number of digits: truncation to zero significant digits is the same as the integer part. For an integer, . Notation The ''integral part'' or ''integer part'' of a number ( in the original) was first defined in 1798 by Adrien-Marie Legendre in his proof of the Legendre's formula. Carl Friedrich Gauss introduced the square bracket notation in his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
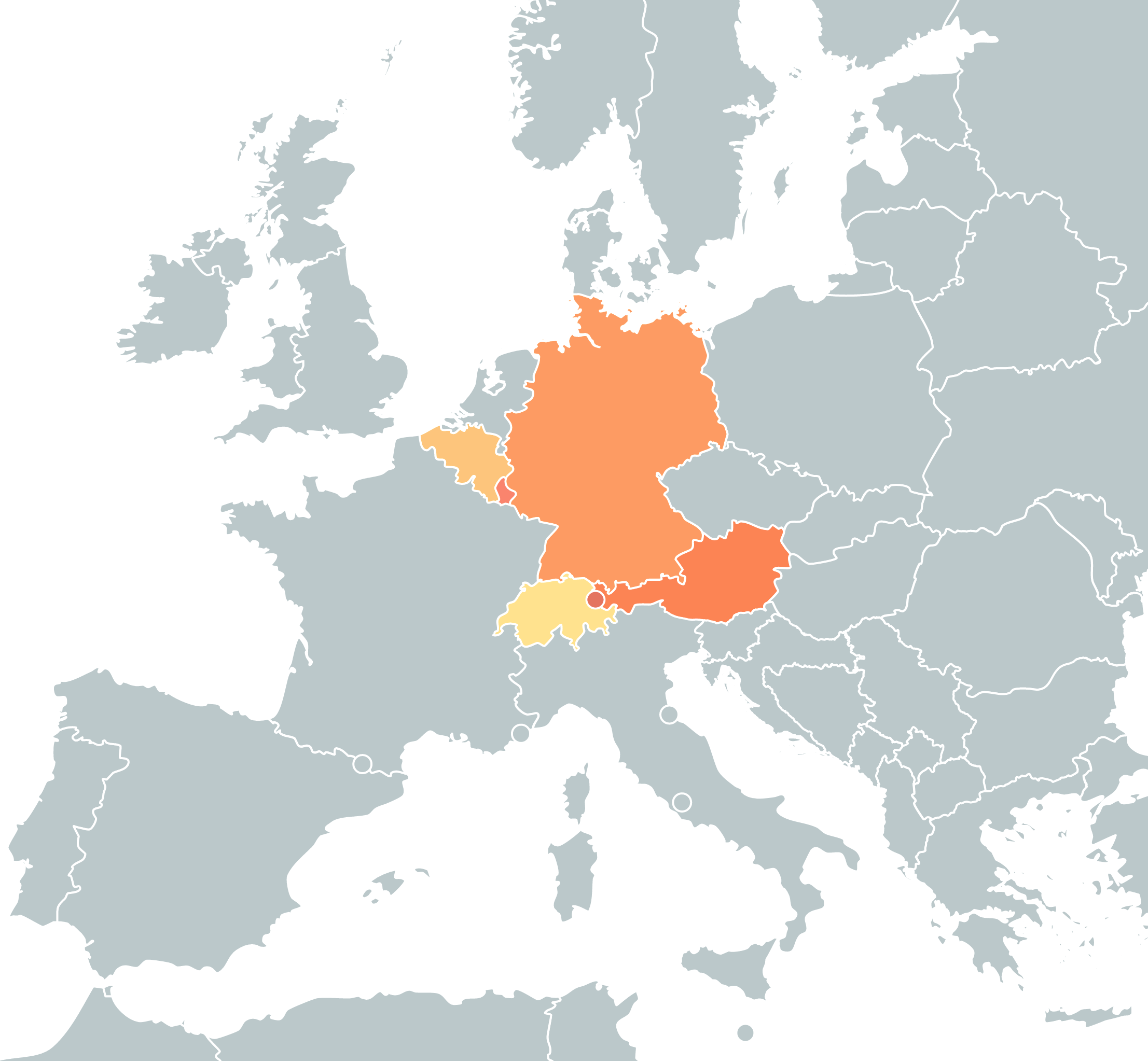
German Language
German ( ) is a West Germanic languages, West Germanic language mainly spoken in Central Europe. It is the most widely spoken and Official language, official or co-official language in Germany, Austria, Switzerland, Liechtenstein, and the Italy, Italian province of South Tyrol. It is also a co-official language of Luxembourg and German-speaking Community of Belgium, Belgium, as well as a national language in Namibia. Outside Germany, it is also spoken by German communities in France (Bas-Rhin), Czech Republic (North Bohemia), Poland (Upper Silesia), Slovakia (Bratislava Region), and Hungary (Sopron). German is most similar to other languages within the West Germanic language branch, including Afrikaans, Dutch language, Dutch, English language, English, the Frisian languages, Low German, Luxembourgish, Scots language, Scots, and Yiddish. It also contains close similarities in vocabulary to some languages in the North Germanic languages, North Germanic group, such as Danish lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |