|
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex valued frequency-domain (the z-domain or z-plane) representation. It can be considered a discrete-time equivalent of the Laplace transform (the ''s-domain'' or ''s-plane''). This similarity is explored in the theory of time-scale calculus. While the continuous-time Fourier transform is evaluated on the s-domain's vertical axis (the imaginary axis), the discrete-time Fourier transform is evaluated along the z-domain's unit circle. The s-domain's left half-plane maps to the area inside the z-domain's unit circle, while the s-domain's right half-plane maps to the area outside of the z-domain's unit circle. In signal processing, one of the means of designing digital filters is to take analog designs, subject them to a bilinear transform which maps them from the s-domain to the z-domain, and then produce the digital filter by in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex-valued frequency domain, also known as ''s''-domain, or ''s''-plane). The transform is useful for converting derivative, differentiation and integral, integration in the time domain into much easier multiplication and Division (mathematics), division in the Laplace domain (analogous to how logarithms are useful for simplifying multiplication and division into addition and subtraction). This gives the transform many applications in science and engineering, mostly as a tool for solving linear differential equations and dynamical systems by simplifying ordinary differential equations and integral equations into algebraic equation, algebraic polynomial equations, and by simplifyin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
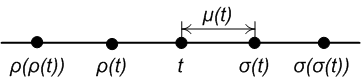
Time-scale Calculus
In mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid systems. It has applications in any field that requires simultaneous modelling of discrete and continuous data. It gives a new definition of a derivative such that if one differentiates a function defined on the real numbers then the definition is equivalent to standard differentiation, but if one uses a function defined on the integers then it is equivalent to the forward difference operator. History Time-scale calculus was introduced in 1988 by the German mathematician Stefan Hilger. However, similar ideas have been used before and go back at least to the introduction of the Riemann–Stieltjes integral, which unifies sums and integrals. Dynamic equations Many results concerning differential equations carry over quite eas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as because it is a one-dimensional unit -sphere. If is a point on the unit circle's circumference, then and are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, and satisfy the equation x^2 + y^2 = 1. Since for all , and since the reflection of any point on the unit circle about the - or -axis is also on the unit circle, the above equation holds for all points on the unit circle, not only those in the first quadrant. The interior of the unit circle is called the open unit disk, while the interior of the unit circle combined with the unit circle itself is called the closed unit disk. One may also use other notions of "dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurent Series
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass had previously described it in a paper written in 1841 but not published until 1894. Definition The Laurent series for a complex function f(z) about an arbitrary point c is given by f(z) = \sum_^\infty a_n(z-c)^n, where the coefficients a_n are defined by a contour integral that generalizes Cauchy's integral formula: a_n =\frac\oint_\gamma \frac \, dz. The path of integration \gamma is counterclockwise around a Jordan curve enclosing c and lying in an annulus A in which f(z) is holomorphic ( analytic). The expansion for f(z) will then be valid anywhere inside the annulus. The annulus is shown in red in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eliahu I
Eliahu or Eliyahu is a masculine Hebrew given name and surname of biblical origin. It means "My God is Yahweh" and derives from the prophet Elijah who, according to the Bible, lived during the reign of King Ahab (9th century BCE). People named Eliahu or Eliyahu, include: Given name Eliahu * Eliahu Eilat (1903–1990), Israeli diplomat, Orientalist and President of the Hebrew University of Jerusalem * Eliahu Gat (1919–1987), Israeli landscape painter * Eliahu Inbal (born 1936), Israeli conductor * Eliahu Nissim (1933-2020), Israeli former professor of aeronautical engineering and former President of the Open University of Israel * Eliahu Stern (born 1948), Israeli professor emeritus of geography and planning Eliyahu * Eliyahu Bet-Zuri (1922–1945), Jewish Lehi member and assassin * Eliyahu Berligne (1866–1959), a founder of Tel Aviv, a member of the Yishuv in Mandate Palestine and a signatory of the Israeli declaration of independence * Eli Cohen (1924–1965), Israel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generating Functions
In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Generating functions are often expressed in closed form (rather than as a series), by some expression involving operations on the formal series. There are various types of generating functions, including ordinary generating functions, exponential generating functions, Lambert series, Bell series, and Dirichlet series. Every sequence in principle has a generating function of each type (except that Lambert and Dirichlet series require indices to start at 1 rather than 0), but the ease with which they can be handled may differ considerably. The particular generating function, if any, that is most useful in a given context will depend upon the nature of the sequence and the details of the problem being addressed. Generating functions are sometimes called generating series, in that a series of terms can be said to be the generator of its sequence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abraham De Moivre
Abraham de Moivre FRS (; 26 May 166727 November 1754) was a French mathematician known for de Moivre's formula, a formula that links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He moved to England at a young age due to the religious persecution of Huguenots in France which reached a climax in 1685 with the Edict of Fontainebleau. He was a friend of Isaac Newton, Edmond Halley, and James Stirling (mathematician), James Stirling. Among his fellow Huguenot exiles in England, he was a colleague of the editor and translator Pierre des Maizeaux. De Moivre wrote a book on probability theory, ''The Doctrine of Chances'', said to have been prized by gamblers. De Moivre first discovered Binet's formula, the closed-form expression for Fibonacci numbers linking the ''n''th power of the golden ratio ''φ'' to the ''n''th Fibonacci number. He also was the first to postulate the central limit theorem, a cornerstone of probability theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficients
In mathematics, a coefficient is a multiplicative factor involved in some term of a polynomial, a series, or any other type of expression. It may be a number without units, in which case it is known as a numerical factor. It may also be a constant with units of measurement, in which it is known as a constant multiplier. In general, coefficients may be any expression (including variables such as , and ). When the combination of variables and constants is not necessarily involved in a product, it may be called a ''parameter''. For example, the polynomial 2x^2-x+3 has coefficients 2, −1, and 3, and the powers of the variable x in the polynomial ax^2+bx+c have coefficient parameters a, b, and c. A , also known as constant term or simply constant, is a quantity either implicitly attached to the zeroth power of a variable or not attached to other variables in an expression; for example, the constant coefficients of the expressions above are the number 3 and the parameter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John R
John R. (born John Richbourg, August 20, 1910 – February 15, 1986) was an American radio disc jockey who attained fame in the 1950s and 1960s for playing rhythm and blues music on Nashville radio station WLAC. He was also a notable record producer and artist manager. Richbourg was arguably the most popular and charismatic of the four announcers at WLAC who showcased popular African-American music in nightly programs from the late 1940s to the early 1970s. (The other three were Gene Nobles, Herman Grizzard, and Bill "Hoss" Allen.) Later rock music disc jockeys, such as Alan Freed and Wolfman Jack, mimicked Richbourg's practice of using speech that simulated African-American street language of the mid-twentieth century. Richbourg's highly stylized approach to on-air presentation of both music and advertising earned him popularity, but it also created identity confusion. Because Richbourg and fellow disc jockey Allen used African-American speech patterns, many listeners thought t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if for every x_0 in its domain, its Taylor series about x_0 converges to the function in some neighborhood of x_0 . This is stronger than merely being infinitely differentiable at x_0 , and therefore having a well-defined Taylor series; the Fabius function provides an example of a function that is infinitely differentiable but not analytic. Definitions Formally, a function f is ''real analytic'' on an open set D in the real line if for any x_0\in D one can write f(x) = \sum_^\infty a_ \left( x-x_0 \right)^ = a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + \cdots in which the coefficients a_0, a_1, \dots a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |