|
Word RAM
In theoretical computer science, the word RAM (word random-access machine) model is a model of computation in which a random-access machine does arithmetic and bitwise operations on a word of bits. Michael Fredman and Dan Willard created it in 1990 to simulate programming languages like C. Model The word RAM model is an abstract machine similar to a random-access machine, but with finite memory and word-length. It works with words of size up to bits, meaning it can store integers up to 2^w-1. Because the model assumes that the word size matches the problem size, that is, for a problem of size , w \ge \log n, the word RAM model is a transdichotomous model. The model allows both arithmetic operations and bitwise operations including logical shifts to be done in constant time (the precise instruction set assumed by an algorithm or proof using the model may vary). Algorithms and data structures In the word RAM model, integer sorting can be done fairly efficiently. Yijie Han an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Computer Science
Theoretical computer science is a subfield of computer science and mathematics that focuses on the Abstraction, abstract and mathematical foundations of computation. It is difficult to circumscribe the theoretical areas precisely. The Association for Computing Machinery, ACM's Special Interest Group on Algorithms and Computation Theory (SIGACT) provides the following description: History While logical inference and mathematical proof had existed previously, in 1931 Kurt Gödel proved with his incompleteness theorem that there are fundamental limitations on what statements could be proved or disproved. Information theory was added to the field with A Mathematical Theory of Communication, a 1948 mathematical theory of communication by Claude Shannon. In the same decade, Donald Hebb introduced a mathematical model of Hebbian learning, learning in the brain. With mounting biological data supporting this hypothesis with some modification, the fields of neural networks and para ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mikkel Thorup
Mikkel Thorup (born 1965) is a Danish computer scientist working at University of Copenhagen. He completed his undergraduate education at Technical University of Denmark and his doctoral studies at Oxford University in 1993. From 1993 to 1998, he was at University of Copenhagen and from 1998 to 2013 he was at AT&T Labs-Research in New Jersey. Since 2013 he has been at the University of Copenhagen as a Professor and Head of Center for Efficient Algorithms and Data Structures (EADS). Thorup's main work is in algorithms and data structures. One of his best-known results is a linear-time algorithm for the single-source shortest paths problem in undirected graphs (Thorup, 1999). With Mihai Pătraşcu he has shown that simple tabulation hashing schemes achieve the same or similar performance criteria as hash families that have higher independence in worst case, while permitting speedier implementations. Thorup has been editor of the area algorithm and data structures for Journal of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cell-probe Model
In computer science, the cell-probe model is a model of computation similar to the random-access machine, except that all operations are free except memory access. This model is useful for proving lower bounds of algorithms for data structure problems. Overview The cell-probe model is a modification of the random-access machine model, in which computational cost is only assigned to accessing memory cells. The model is intended for proving lower bounds on the complexity of data structure problems. One type of such problems has two phases: the preprocessing phase and the query phase. The input to the first phase, the preprocessing phase, is a set of data from which to build some structure from memory cells. The input to the second phase, the query phase, is a query parameter. The query has to consult the data structure in order to compute its result; for example, a query may be asked to determine if the query parameter was included in the original input data set. Another type ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Range Searching
In computer science, the range searching problem consists of processing a set ''S'' of objects, in order to determine which objects from ''S'' intersect with a query object, called the ''range''. For example, if ''S'' is a set of points corresponding to the coordinates of several cities, find the subset of cities within a given range of latitudes and longitudes. The range searching problem and the data structures that solve it are a fundamental topic of computational geometry. Applications of the problem arise in areas such as Geographic information system, geographical information systems (GIS), computer-aided design (CAD) and databases. Variations There are several variations of the problem, and different data structures may be necessary for different variations. In order to obtain an efficient solution, several aspects of the problem need to be specified: * Object types: Algorithms depend on whether ''S'' consists of Point (geometry), points, line (geometry), lines, line seg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Tree
An exponential tree is a type of search tree In computer science, a search tree is a tree data structure used for locating specific keys from within a set. In order for a tree to function as a search tree, the key for each node must be greater than any keys in subtrees on the left, and les ... where the number of children of its nodes decreases doubly- exponentially with increasing depth. Values are stored only in the leaf nodes. Each node contains a splitter, a value less than or equal to all values in the subtree which is used during search. Exponential trees use another data structure in inner nodes containing the splitters from children, allowing fast lookup. Exponential trees achieve optimal asymptotic complexity on some operations. They have mainly theoretical importance. Tree structure An exponential tree is a rooted tree where every node contains a splitter and every leaf node contains a value. The value may be different from the splitter. An exponential tree with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
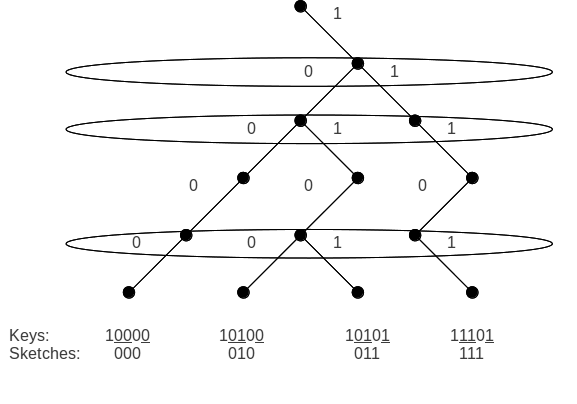
Fusion Tree
In computer science, a fusion tree is a type of tree data structure that implements an associative array on -bit integers on a finite universe, where each of the input integers has size less than 2w and is non-negative. When operating on a collection of Attribute–value pair, key–value pairs, it uses space and performs searches in time, which is asymptotically faster than a traditional self-balancing binary search tree, and also better than the van Emde Boas tree for large values of . It achieves this speed by using certain constant-time operations that can be done on a machine word. Fusion trees were invented in 1990 by Michael Fredman and Dan Willard. Several advances have been made since Fredman and Willard's original 1990 paper. In 1999. it was shown how to implement fusion trees under a model of computation in which all of the underlying operations of the algorithm belong to AC0, AC0, a model of circuit complexity that allows addition and bitwise Boolean operations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Y-fast Trie
In computer science, a y-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time ''O''(log log ''M''), using ''O''(''n'') space, where ''n'' is the number of stored values and ''M'' is the maximum value in the domain. The structure was proposed by Dan Willard in 1982 to decrease the ''O''(''n'' log ''M'') space used by an x-fast trie. Structure A y-fast trie consists of two data structures: the top half is an x-fast trie and the lower half consists of a number of balanced binary trees. The keys are divided into groups of ''O''(log ''M'') consecutive elements and for each group a balanced binary search tree is created. To facilitate efficient insertion and deletion, each group contains at least (log ''M'')/4 and at most 2 log ''M'' elements. For each balanced binary search tree a representative ''r'' is chosen. These representatives are stored in the x-fast ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Predecessor Problem
In computer science, the predecessor problem involves maintaining a set of items to, given an element, efficiently query which element precedes or succeeds that element in an order. Data structures used to solve the problem include balanced binary search trees, van Emde Boas trees, and fusion trees. In the static predecessor problem, the set of elements does not change, but in the dynamic predecessor problem, insertions into and deletions from the set are allowed. The predecessor problem is a simple case of the nearest neighbor problem, and data structures that solve it have applications in problems like integer sorting. Definition The problem consists of maintaining a set , which contains a subset of integers. Each of these integers can be stored with a word size of , implying that U \le 2^w. Data structures that solve the problem support these operations: * predecessor(x), which returns the largest element in strictly smaller than * successor(x), which returns the smalle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Running Time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is genera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deterministic Algorithm
In computer science, a deterministic algorithm is an algorithm that, given a particular input, will always produce the same output, with the underlying machine always passing through the same sequence of states. Deterministic algorithms are by far the most studied and familiar kind of algorithm, as well as one of the most practical, since they can be run on real machines efficiently. Formally, a deterministic algorithm computes a mathematical function; a function has a unique value for any input in its domain, and the algorithm is a process that produces this particular value as output. Formal definition Deterministic algorithms can be defined in terms of a state machine: a ''state'' describes what a machine is doing at a particular instant in time. State machines pass in a discrete manner from one state to another. Just after we enter the input, the machine is in its ''initial state'' or ''start state''. If the machine is deterministic, this means that from this point onwar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big O Notation
Big ''O'' notation is a mathematical notation that describes the asymptotic analysis, limiting behavior of a function (mathematics), function when the Argument of a function, argument tends towards a particular value or infinity. Big O is a member of a #Related asymptotic notations, family of notations invented by German mathematicians Paul Gustav Heinrich Bachmann, Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for '':wikt:Ordnung#German, Ordnung'', meaning the order of approximation. In computer science, big O notation is used to Computational complexity theory, classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetic function, arithmetical function and a better understood approximation; one well-known exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Time
In computational complexity theory, the average-case complexity of an algorithm is the amount of some computational resource (typically time) used by the algorithm, averaged over all possible inputs. It is frequently contrasted with worst-case complexity which considers the maximal complexity of the algorithm over all possible inputs. There are three primary motivations for studying average-case complexity. First, although some problems may be intractable in the worst-case, the inputs which elicit this behavior may rarely occur in practice, so the average-case complexity may be a more accurate measure of an algorithm's performance. Second, average-case complexity analysis provides tools and techniques to generate hard instances of problems which can be utilized in areas such as cryptography and derandomization. Third, average-case complexity allows discriminating the most efficient algorithm in practice among algorithms of equivalent best case complexity (for instance Quicksort). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |