Fusion Tree on:
[Wikipedia]
[Google]
[Amazon]
In
 An important property of the sketch function is that it preserves the order of the keys. That is, for any two keys . So, for the entire range of keys, sketch(x0)
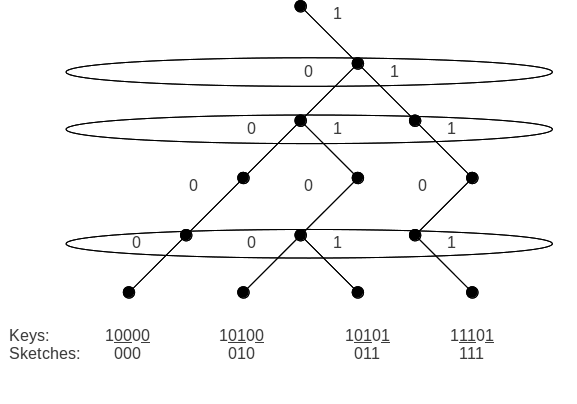
An important property of the sketch function is that it preserves the order of the keys. That is, for any two keys . So, for the entire range of keys, sketch(x0)1)<...k-1) because if the binary tree like path is followed the nodes will be ordered in such a manner that x01<...k-1.
1)<...k-1).
Some preprocessing is needed to determine the correct multiplication constant. Each sketch bit in location ''b''''i'' will get shifted to ''b''''i'' + ''m''''i'' via a multiplication by ''m'' = 2''m''''i''. For the approximate sketch to work, the following three properties must hold:
# ''b''''i'' + ''m''''j'' are distinct for all pairs (''i'', ''j''). This will ensure that the sketch bits are uncorrupted by the multiplication.
# ''b''''i'' + ''m''''i'' is a strictly increasing function of ''i''. That is, the order of the sketch bits is preserved even in x'.m.
# (''b''''r'' + ''m''''r'') - (''b''1 + ''m''1) ≤ ''r''4. That is, the sketch bits are packed into a range of size at most ''r''4, where r ≤ O(w1/5).
An inductive argument shows how the ''m''''i'' can be constructed. Let ''m''1 = ''w'' − ''b''1. Suppose that 1 < ''t'' ≤ ''r'' and that ''m''1, ''m''2... ''m''''t-1'' have already been chosen. Then pick the smallest integer ''m''''t'' such that both properties (1) and (2) are satisfied. Property (1) requires that ''m''''t'' ≠ ''b''''i'' − ''b''''j'' + ''m''''l'' for all 1 ≤ ''i'', ''j'' ≤ ''r'' and 1 ≤ ''l'' ≤ ''t''-1. Thus, there are less than ''tr''2 ≤ ''r''3 values that ''m''''t'' must avoid. Since ''m''''t'' is chosen to be minimal, (''b''''t'' + ''m''''t'') ≤ (''b''''t''-1 + ''m''''t''-1) + ''r''3. This implies Property (3).
The approximate sketch is thus computed as follows:
# Mask out all but the sketch bits with a bitwise AND between ''x'' and .
# Multiply the key by the predetermined constant ''m'' as calculated above. This operation actually requires two machine words, but this can still be done in constant time.
# Mask out all but the shifted sketch bits. These are now contained in a contiguous block of at most ''r''4 < ''w''4/5 bits.
MIT CS 6.897: Advanced Data Structures: Lecture 4, Fusion Trees
Prof. Erik Demaine (Spring 2003)
MIT CS 6.897: Advanced Data Structures: Lecture 5, More fusion trees; self-organizing data structures, move-to-front, static optimality
Prof. Erik Demaine (Spring 2003)
MIT CS 6.851: Advanced Data Structures: Lecture 13, Fusion Tree notes
Prof. Erik Demaine (Spring 2007)
MIT CS 6.851: Advanced Data Structures: Lecture 12, Fusion Tree notes
Prof. Erik Demaine (Spring 2012) {{CS-Trees Trees (data structures) Associative arrays
computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includin ...
, a fusion tree is a type of tree data structure
In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children (depending on the type of tree), but must be con ...
that implements an associative array
In computer science, an associative array, map, symbol table, or dictionary is an abstract data type that stores a collection of (key, value) pairs, such that each possible key appears at most once in the collection. In mathematical terms an ...
on -bit integers on a finite universe, where each of the input integer has size less than 2w and is non-negative. When operating on a collection of key–value pairs, it uses space and performs searches in time, which is asymptotically faster than a traditional self-balancing binary search tree
In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height (maximal number of levels below the root) small in the face of arbitrary item insertions and deletions.Donald ...
, and also better than the van Emde Boas tree for large values of . It achieves this speed by using certain constant-time operations that can be done on a machine word
In computing, a word is the natural unit of data used by a particular processor design. A word is a fixed-sized datum handled as a unit by the instruction set or the hardware of the processor. The number of bits or digits in a word (the ''wor ...
. Fusion trees were invented in 1990 by Michael Fredman
Michael Lawrence Fredman is an emeritus professor at the Computer Science Department at Rutgers University, United States. He earned his Ph.D. degree from Stanford University in 1972 under the supervision of Donald Knuth. He was a member of the ...
and Dan Willard
Dan Edward Willard is an American computer scientist and logician, and is a professor of computer science at the University at Albany.
Education and career
Willard did his undergraduate studies in mathematics at Stony Brook University, graduating ...
.
Several advances have been made since Fredman and Willard's original 1990 paper. In 1999 it was shown how to implement fusion trees under a model of computation in which all of the underlying operations of the algorithm belong to AC0, a model of circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of the Boolean circuits that compute them. A related notion is the ci ...
that allows addition and bitwise Boolean operations but does not allow the multiplication operations used in the original fusion tree algorithm. A dynamic version of fusion trees using hash tables
In computing, a hash table, also known as hash map, is a data structure that implements an associative array or dictionary. It is an abstract data type that maps keys to values. A hash table uses a hash function to compute an ''index'', ...
was proposed in 1996 which matched the original structure's runtime in expectation. Another dynamic version using exponential tree was proposed in 2007 which yields worst-case runtimes of per operation. It remains open whether dynamic fusion trees can achieve per operation with high probability.
This data structure is helpful for predecessor and successor search operations which provide an output as the greatest key value smaller than the queried key or the smallest key value larger than the queried key, respectively. The partial result of most significant bit locator in constant time has also helped a lot of further research. The chief idea why this work is efficient is because it deploys word-level parallelism, which means that the computation on multiple words takes place simultaneously, making the number of overall operations way less than they should be. Other operations that can be performed on this data structure are add a key, and remove a key.
How it works
A fusion tree is essentially aB-tree
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for ...
with branching factor of (any small exponent is also possible as it will not have a great impact on the height of the tree), which gives it a height of . To achieve the desired runtimes for updates and queries, the fusion tree must be able to search a node containing up to keys in constant time. This is done by compressing ("sketching") the keys so that all can fit into one machine word, which in turn allows comparisons to be done in parallel. So, a series of computations involving sketching, parallel comparison and most significant bit index locator, help reach the required solution.
Sketching
Sketching is the method by which each -bit key at a node containing keys is compressed into only bits. Each key may be thought of as a path in the full binary tree of height starting at the root and ending at the leaf corresponding to . This path can be processed by recursively searching the left child of ''i'' if the ''ith'' bit is 0, and the right child if it is 1, generally, until all bits are scanned. To distinguish two paths, it suffices to look at their branching point (the first bit where any two keys differ). As there are a maximum of ''k'' keys, there will not be more than ''k-1'' branching points, which means that no more than ''k-1'' bits are required to identify a key. And hence, no sketch will have more than ''k-1'' bits. An important property of the sketch function is that it preserves the order of the keys. That is, for any two keys . So, for the entire range of keys, sketch(x0)
An important property of the sketch function is that it preserves the order of the keys. That is, for any two keys . So, for the entire range of keys, sketch(x0)Approximating the sketch
If the locations of the sketch bits are ''b''1 < ''b''2 < ··· < ''b''''r'', then the sketch of the key ''x''''w''-1···''x''1''x''0 is the ''r''-bit integer . With only standard word operations, such as those of theC programming language
''The C Programming Language'' (sometimes termed ''K&R'', after its authors' initials) is a computer programming book written by Brian Kernighan and Dennis Ritchie, the latter of whom originally designed and implemented the language, as well as ...
, it is difficult to directly compute the perfect sketch of a key in constant time. Instead, the sketch bits can be packed into a range of size at most ''r''4, using bitwise AND
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic operat ...
and multiplication, called the approximate sketch, which does have all the important bits but also some additional useless bits spread out in a predictable pattern. The bitwise AND operation serves as a mask to remove all these non-sketch bits from the key, while the multiplication shifts the sketch bits into a small range. Like the "perfect" sketch, the approximate sketch also preserves the order of the keys and means that sketch(x0)Parallel comparison
The purpose of the compression achieved by sketching is to allow all of the keys to be stored in one ''w''-bit word. Let the ''node sketch'' of a node be the bit string :1sketch(''x''1)1sketch(''x''2)...1sketch(''x''''k'')
Here, all sketch words are clubbed together in one string by prepending a set bit to each of them. We can assume that the sketch function uses exactly ''b'' ≤ ''r''4 bits. Then each block uses 1 + ''b'' ≤ ''w''4/5 bits, and since ''k'' ≤ ''w''1/5, the total number of bits in the node sketch is at most ''w''.
A brief notational aside: for a bit string ''s'' and nonnegative integer ''m'', let ''s''''m'' denote the concatenation of ''s'' to itself ''m'' times. If ''t'' is also a bit string ''st'' denotes the concatenation of ''t'' to ''s''.
The node sketch makes it possible to search the keys for any ''b''-bit integer ''y''. Let ''z'' = (0''y'')''k'', which can be computed in constant time (multiply ''y'' by the constant (0''b''1)''k''), to make it as long as the node sketch such that each word in the node sketch can be compared with the query integer ''y'' in one operation, demonstrating word-level parallelism. If ''y'' were 5 bits long, it would be multiplied by 000001....000001 to get sketch(y)k. The difference between sketch(xi) and 0y results in the leading bit for each block to be 1, if and only if sketch(y) sketch(xi). We can thus compute the smallest index ''i'' such that sketch(''x''''i'') ≥ ''y'' as follows:
# Subtract ''z'' from the node sketch.
# Take the bitwise AND of the difference and the constant (10''b'')''k''. This clears all but the leading bit of each block.
# Find the most significant bit
In computing, bit numbering is the convention used to identify the bit positions in a binary number.
Bit significance and indexing
In computing, the least significant bit (LSB) is the bit position in a binary integer representing the binary ...
of the result, to identify the exact index of transition from elements with sketch smaller than the query sketch to those greater than the query sketch.
# Compute ''i,'' the rank of the sketch, using the fact that the leading bit of the ''i''-th block has index ''i''(''b''+1).
Desketching
For an arbitrary query ''q'', parallel comparison computes the index ''i'' such that :sketch(''x''''i''-1) ≤ sketch(''q'') ≤ sketch(''x''''i'')
Unfortunately, this does give the exact predecessor or successor of ''q'', because the location of the sketch of ''q'' among the sketches of all the values may not be the same as the location of ''q'' in all the actual values. What is true is that, among all of the keys, either ''x''''i''-1 or ''x''''i'' has the longest common prefix with ''q''. This is because any key ''y'' with a longer common prefix with ''q'' would also have more sketch bits in common with ''q'', and thus sketch(''y'') would be closer to sketch(''q'') than any sketch(''x''''j'').
The length longest common prefix between two ''w''-bit integers ''a'' and ''b'' can be computed in constant time by finding the most significant bit of the bitwise XOR between ''a'' and ''b''. This can then be used to mask out all but the longest common prefix.
Note that ''p'' identifies exactly where ''q'' branches off from the set of keys. If the next bit of ''q'' is 0, then the successor of ''q'' is contained in the ''p''1 subtree, and if the next bit of ''q'' is 1, then the predecessor of ''q'' is contained in the ''p''0 subtree. This suggests the following algorithm for determining the exact location of ''q'':
# Use parallel comparison to find the index ''i'' such that sketch(''x''''i''-1) ≤ sketch(''q'') ≤ sketch(''x''''i'').
# Compute the longest common prefix ''p'' of ''q'' and either ''x''''i''-1 or ''x''''i'' (taking the longer of the two).
# Let ''l''-1 be the length of the longest common prefix ''p''.
## If the ''l''-th bit of ''q'' is 0, let ''e'' = ''p''10''w''-''l''. Use parallel comparison to search for the successor of sketch(''e''). This is the actual predecessor of ''q''.
## If the ''l''-th bit of ''q'' is 1, let ''e'' = ''p''01''w''-''l''. Use parallel comparison to search for the predecessor of sketch(''e''). This is the actual successor of ''q''.
# Once either the predecessor or successor of ''q'' is found, the exact position of ''q'' among the set of keys is determined.
Fusion hashing
An application of fusion trees tohash table
In computing, a hash table, also known as hash map, is a data structure that implements an associative array or dictionary. It is an abstract data type that maps keys to values. A hash table uses a hash function to compute an ''index'', ...
s was given by Willard, who describes a data structure for hashing in which an outer-level hash table with hash chaining is combined with a fusion tree representing each hash chain.
In hash chaining, in a hash table with a constant load factor, the average size of a chain is constant, but additionally with high probability all chains have size , where is the number of hashed items.
This chain size is small enough that a fusion tree can handle searches and updates within it in constant time per operation. Therefore, the time for all operations in the data structure is constant with high probability.
More precisely, with this data structure, for every inverse- quasipolynomial probability , there is a constant such that the probability that there exists an operation that exceeds time is at most ..
References
External links
MIT CS 6.897: Advanced Data Structures: Lecture 4, Fusion Trees
Prof. Erik Demaine (Spring 2003)
MIT CS 6.897: Advanced Data Structures: Lecture 5, More fusion trees; self-organizing data structures, move-to-front, static optimality
Prof. Erik Demaine (Spring 2003)
MIT CS 6.851: Advanced Data Structures: Lecture 13, Fusion Tree notes
Prof. Erik Demaine (Spring 2007)
MIT CS 6.851: Advanced Data Structures: Lecture 12, Fusion Tree notes
Prof. Erik Demaine (Spring 2012) {{CS-Trees Trees (data structures) Associative arrays