|
Wilks' Lambda Distribution
In statistics, Wilks' lambda distribution (named for Samuel S. Wilks), is a probability distribution used in multivariate hypothesis testing, especially with regard to the likelihood-ratio test and multivariate analysis of variance (MANOVA). Definition Wilks' lambda distribution is defined from two independent Wishart distributed variables as the ratio distribution of their determinants, given :\mathbf \sim W_p(\Sigma, m) \qquad \mathbf \sim W_p(\Sigma, n) independent and with m \ge p :\lambda = \frac = \frac \sim \Lambda(p,m,n) where ''p'' is the number of dimensions. In the context of likelihood-ratio tests ''m'' is typically the error degrees of freedom, and ''n'' is the hypothesis degrees of freedom, so that n+m is the total degrees of freedom. Approximations Computations or tables of the Wilks' distribution for higher dimensions are not readily available and one usually resorts to approximations. One approximation is attributed to M. S. Bartlett and works for large ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The Royal Statistical Society
The ''Journal of the Royal Statistical Society'' is a peer-reviewed scientific journal of statistics. It comprises three series and is published by Wiley for the Royal Statistical Society. History The Statistical Society of London was founded in 1834, but would not begin producing a journal for four years. From 1834 to 1837, members of the society would read the results of their studies to the other members, and some details were recorded in the proceedings. The first study reported to the society in 1834 was a simple survey of the occupations of people in Manchester, England. Conducted by going door-to-door and inquiring, the study revealed that the most common profession was mill-hands, followed closely by weavers. When founded, the membership of the Statistical Society of London overlapped almost completely with the statistical section of the British Association for the Advancement of Science. In 1837 a volume of ''Transactions of the Statistical Society of London'' were wri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hotelling's T-squared Distribution
In statistics, particularly in hypothesis testing, the Hotelling's ''T''-squared distribution (''T''2), proposed by Harold Hotelling, is a multivariate probability distribution that is tightly related to the ''F''-distribution and is most notable for arising as the distribution of a set of sample statistics that are natural generalizations of the statistics underlying the Student's ''t''-distribution. The Hotelling's ''t''-squared statistic (''t''2) is a generalization of Student's ''t''-statistic that is used in multivariate hypothesis testing. Motivation The distribution arises in multivariate statistics in undertaking tests of the differences between the (multivariate) means of different populations, where tests for univariate problems would make use of a ''t''-test. The distribution is named for Harold Hotelling, who developed it as a generalization of Student's ''t''-distribution. Definition If the vector d is Gaussian multivariate-distributed with zero mean and unit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
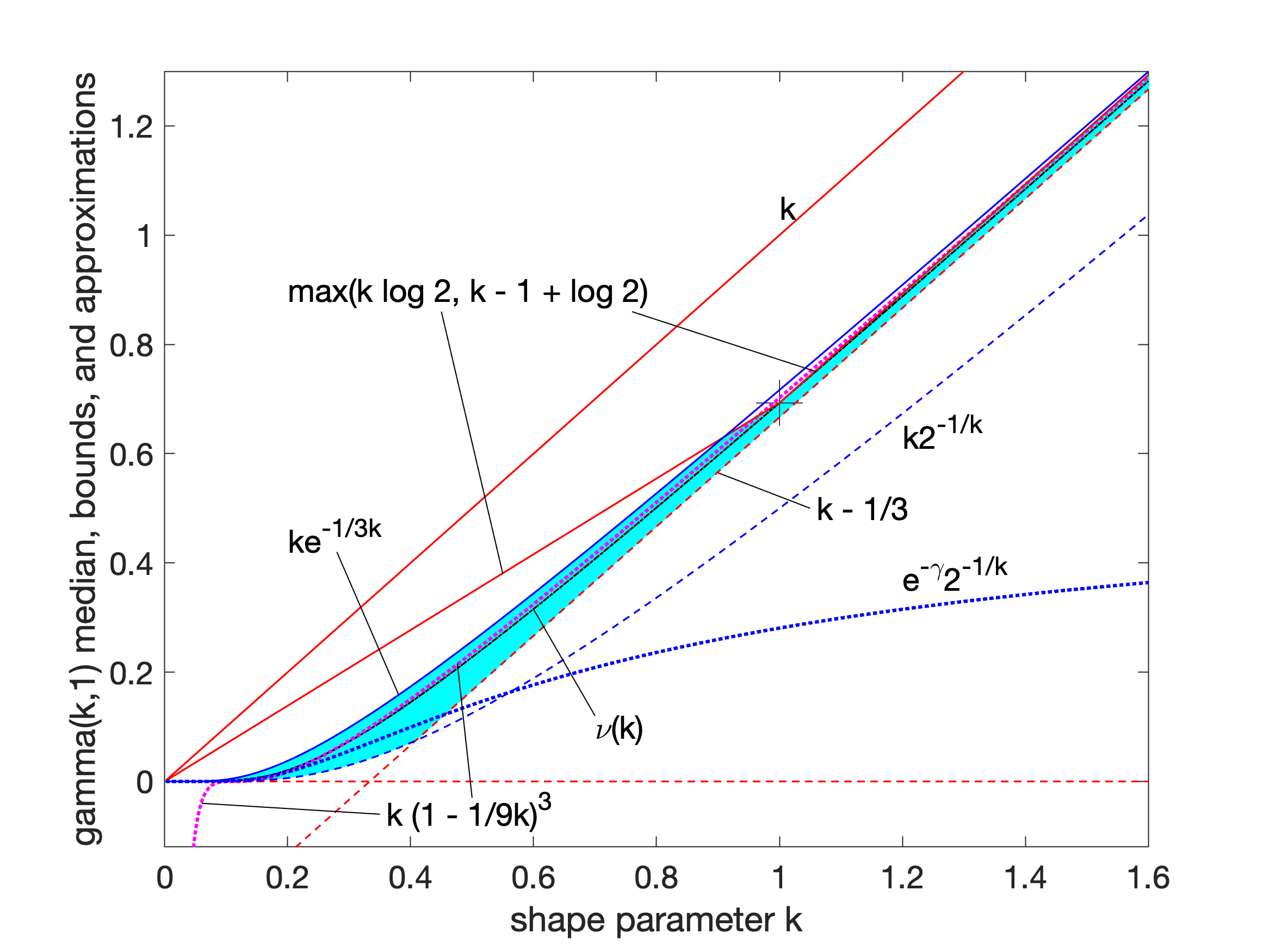
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common in econo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Distribution
In probability and statistics, the Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), often denoted \operatorname(\boldsymbol\alpha), is a family of continuous multivariate probability distributions parameterized by a vector \boldsymbol\alpha of positive reals. It is a multivariate generalization of the beta distribution, (Chapter 49: Dirichlet and Inverted Dirichlet Distributions) hence its alternative name of multivariate beta distribution (MBD). Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact, the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution. The infinite-dimensional generalization of the Dirichlet distribution is the ''Dirichlet process''. Definitions Probability density function The Dirichlet distribution of order ''K'' ≥ 2 with parameters ''α''1, ..., ''α''''K'' > 0 has a probability density function with respect to Lebesgue m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the chi-squared distribution (also chi-square or \chi^2-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution. The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tests a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-distribution
In probability theory and statistics, the ''F''-distribution or F-ratio, also known as Snedecor's ''F'' distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor) is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other ''F''-tests. Definition The F-distribution with ''d''1 and ''d''2 degrees of freedom is the distribution of : X = \frac where S_1 and S_2 are independent random variables with chi-square distributions with respective degrees of freedom d_1 and d_2. It can be shown to follow that the probability density function (pdf) for ''X'' is given by : \begin f(x; d_1,d_2) &= \frac \\ pt&=\frac \left(\frac\right)^ x^ \left(1+\frac \, x \right)^ \end for real ''x'' > 0. Here \mathrm is the beta function. In many applications, the parameters ''d''1 and ''d''2 are positive integers, but the distribution is well-define ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Distribution
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval , 1in terms of two positive parameters, denoted by ''alpha'' (''α'') and ''beta'' (''β''), that appear as exponents of the random variable and control the shape of the distribution. The beta distribution has been applied to model the behavior of random variables limited to intervals of finite length in a wide variety of disciplines. The beta distribution is a suitable model for the random behavior of percentages and proportions. In Bayesian inference, the beta distribution is the conjugate prior probability distribution for the Bernoulli, binomial, negative binomial and geometric distributions. The formulation of the beta distribution discussed here is also known as the beta distribution of the first kind, whereas ''beta distribution of the second kind'' is an alternative name for the beta prime distribution. The generalization to mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bulletin De L'Institut International De Statistique
''Bulletin of the International Statistical Institute'' (''Bulletin de l'Institut international de statistique'') is a journal published with the proceedings of the biennial meeting of the International Statistical Institute The International Statistical Institute (ISI) is a professional association of statisticians. It was founded in 1885, although there had been international statistical congresses since 1853. The institute has about 4,000 elected members from gov .... It first appeared in 1886. References {{Reflist Statistics journals Biennial journals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the chi-squared distribution (also chi-square or \chi^2-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution. The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tests a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kanti Mardia
Kantilal Vardichand "Kanti" Mardia (born 1935) is an Indian-British statistician specialising in directional statistics, multivariate analysis, geostatistics, statistical bioinformatics and statistical shape analysis. He was born in Sirohi, Rajasthan, India in a Jain family and now resides and works in Leeds. He is known for his series of tests of multivariate normality based measures of multivariate skewness and kurtosis as well as work on the statistical measures of shape. Life and career Mardia was educated at the Ismail Yusuf College at the University of Bombay (BSc 1955, MSc in statistics 1957), the University of Poona (MSc in pure mathematics 1961), the University of Rajasthan (PhD 1965) and the University of Newcastle Upon Tyne (PhD 1967, DSc 1973). He held academic positions at the Institute of Science, Mumbai and the University of Hull. Mardia was appointed professor of applied statistics and head of the Department of Statistics in the School of Mathematics at the Uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Samuel S
Samuel ''Šəmūʾēl'', Tiberian: ''Šămūʾēl''; ar, شموئيل or صموئيل '; el, Σαμουήλ ''Samouḗl''; la, Samūēl is a figure who, in the narratives of the Hebrew Bible, plays a key role in the transition from the biblical judges to the United Kingdom of Israel under Saul, and again in the monarchy's transition from Saul to David. He is venerated as a prophet in Judaism, Christianity, and Islam. In addition to his role in the Hebrew scriptures, Samuel is mentioned in Jewish rabbinical literature, in the Christian New Testament, and in the second chapter of the Quran (although Islamic texts do not mention him by name). He is also treated in the fifth through seventh books of '' Antiquities of the Jews'', written by the Jewish scholar Josephus in the first century. He is first called "the Seer" in 1 Samuel 9:9. Biblical account Family Samuel's mother was Hannah and his father was Elkanah. Elkanah lived at Ramathaim in the district of Zuph. His geneal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |