|
Weierstrass Factorization Theorem
In mathematics, and particularly in the field of complex analysis, the Weierstrass factorization theorem asserts that every entire function can be represented as a (possibly infinite) product involving its zeroes. The theorem may be viewed as an extension of the fundamental theorem of algebra, which asserts that every polynomial may be factored into linear factors, one for each root. The theorem, which is named for Karl Weierstrass, is closely related to a second result that every sequence tending to infinity has an associated entire function with zeroes at precisely the points of that sequence. A generalization of the theorem extends it to meromorphic functions and allows one to consider a given meromorphic function as a product of three factors: terms depending on the function's zeros and poles, and an associated non-zero holomorphic function. Motivation The consequences of the fundamental theorem of algebra are twofold.. Firstly, any finite sequence \ in the complex plane ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
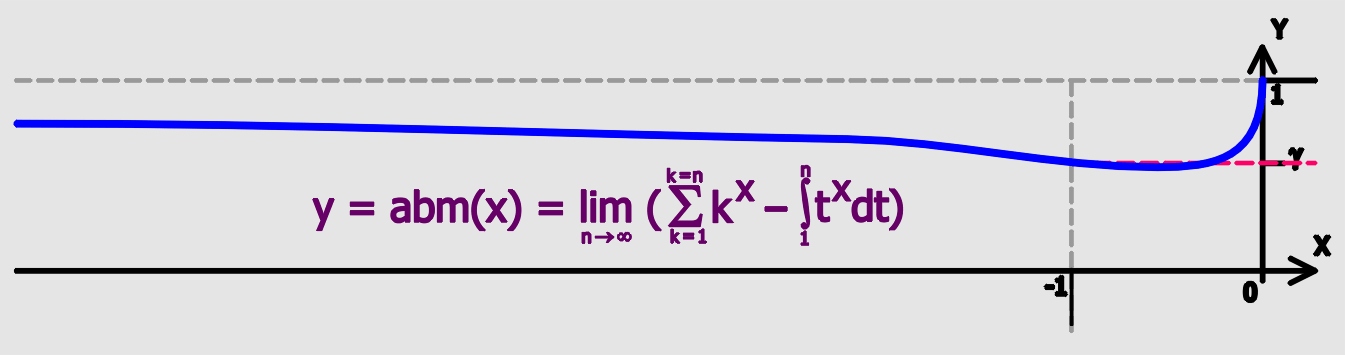
First 5 Weierstrass Factors On The Unit Interval
First or 1st is the ordinal form of the number one (#1). First or 1st may also refer to: *World record, specifically the first instance of a particular achievement Arts and media Music * 1$T, American rapper, singer-songwriter, DJ, and record producer Albums * ''1st'' (album), a 1983 album by Streets * ''1st'' (Rasmus EP), a 1995 EP by The Rasmus, frequently identified as a single * '' 1ST'', a 2021 album by SixTones * ''First'' (Baroness EP), an EP by Baroness * ''First'' (Ferlyn G EP), an EP by Ferlyn G * ''First'' (David Gates album), an album by David Gates * ''First'' (O'Bryan album), an album by O'Bryan * ''First'' (Raymond Lam album), an album by Raymond Lam * ''First'', an album by Denise Ho Songs * "First" (Cold War Kids song), a song by Cold War Kids * "First" (Lindsay Lohan song), a song by Lindsay Lohan * "First", a song by Everglow from ''Last Melody'' * "First", a song by Lauren Daigle * "First", a song by Niki & Gabi * "First", a song by Jonas Brot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wallis Product
In mathematics, the Wallis product for , published in 1656 by John Wallis, states that :\begin \frac & = \prod_^ \frac = \prod_^ \left(\frac \cdot \frac\right) \\ pt& = \Big(\frac \cdot \frac\Big) \cdot \Big(\frac \cdot \frac\Big) \cdot \Big(\frac \cdot \frac\Big) \cdot \Big(\frac \cdot \frac\Big) \cdot \; \cdots \\ \end Proof using integration Wallis derived this infinite product as it is done in calculus books today, by examining \int_0^\pi \sin^n x\,dx for even and odd values of n, and noting that for large n, increasing n by 1 results in a change that becomes ever smaller as n increases. Let :I(n) = \int_0^\pi \sin^n x\,dx. (This is a form of Wallis' integrals.) Integrate by parts: :\begin u &= \sin^x \\ \Rightarrow du &= (n-1) \sin^x \cos x\,dx \\ dv &= \sin x\,dx \\ \Rightarrow v &= -\cos x \end :\begin \Rightarrow I(n) &= \int_0^\pi \sin^n x\,dx \\ pt &= -\sin^x\cos x \Biggl, _0^\pi - \int_0^\pi (-\cos x)(n-1) \sin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mittag-Leffler's Theorem
In complex analysis, Mittag-Leffler's theorem concerns the existence of meromorphic functions with prescribed poles. Conversely, it can be used to express any meromorphic function as a sum of partial fractions. It is sister to the Weierstrass factorization theorem, which asserts existence of holomorphic functions with prescribed zeros. The theorem is named after the Swedish mathematician Gösta Mittag-Leffler who published versions of the theorem in 1876 and 1884. Theorem Let U be an open set in \mathbb C and E \subset U be a subset whose limit points, if any, occur on the boundary of U. For each a in E, let p_a(z) be a polynomial in 1/(z-a) without constant coefficient, i.e. of the form p_a(z) = \sum_^ \frac. Then there exists a meromorphic function f on U whose poles are precisely the elements of E and such that for each such pole a \in E, the function f(z)-p_a(z) has only a removable singularity at a; in particular, the principal part of f at a is p_a(z). Furthermore, any oth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entire Function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function has a root at , then , taking the limit value at , is an entire function. On the other hand, the natural logarithm, the reciprocal function, and the square root are all not entire functions, nor can they be continued analytically to an entire function. A transcendental entire function is an entire function that is not a polynomial. Properties Every entire function can be represented as a power series f(z) = \sum_^\infty a_n z^n that converges everywhere in the complex plane, hen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M \ (z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted simply as \sin \theta and \cos \theta. More generally, the definitions of sine and cosine can be extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and lig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holomorphic Function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex derivative in a neighbourhood is a very strong condition: it implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (''analytic''). Holomorphic functions are the central objects of study in complex analysis. Though the term ''analytic function'' is often used interchangeably with "holomorphic function", the word "analytic" is defined in a broader sense to denote any function (real, complex, or of more general type) that can be written as a convergent power series in a neighbourhood of each point in its domain. That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis. Holomorphic functions are also sometimes referred to as ''regular fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value \infty for infinity. With the Riemann model, the point \infty is near to very large numbers, just as the point 0 is near to very small numbers. The extended complex numbers are useful in complex analysis because they allow for division by zero in some circumstances, in a way that makes expressions such as 1/0=\infty well-behaved. For example, any rational function on the complex plane can be extended to a holomorphic function on the Riemann sphere, with the poles of the rational function mapping to infinity. More generally, any meromorphic function can be thought of as a holomorphic function whose codomain is the Riemann sphere. In geometry, the Riemann sphere is the prototypical example of a Riemann surface, and is one of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Region (mathematics)
In mathematical analysis, a domain or region is a non-empty connected open set in a topological space, in particular any non-empty connected open subset of the real coordinate space or the complex coordinate space . This is a different concept than the domain of a function, though it is often used for that purpose, for example in partial differential equations and Sobolev spaces. The basic idea of a connected subset of a space dates from the 19th century, but precise definitions vary slightly from generation to generation, author to author, and edition to edition, as concepts developed and terms were translated between German, French, and English works. In English, some authors use the term ''domain'', some use the term ''region'', some use both terms interchangeably, and some define the two terms slightly differently; some avoid ambiguity by sticking with a phrase such as ''non-empty connected open subset''. One common convention is to define a ''domain'' as a connected open set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |