|
Woods–Saxon Potential
The Woods–Saxon potential is a mean field potential for the nucleons (protons and neutrons) inside the atomic nucleus, which is used to describe approximately the forces applied on each nucleon, in the nuclear shell model for the structure of the nucleus. The potential is named after Roger D. Woods and David S. Saxon. The form of the potential, in terms of the distance ''r'' from the center of nucleus, is: V(r) = -\frac where ''V''0 (having dimension of energy) represents the potential well depth, ''a'' is a length representing the "surface thickness" of the nucleus, and R = r_0 A^ is the nuclear radius where and ''A'' is the mass number. Typical values for the parameters are: , . For large atomic number ''A'' this potential is similar to a potential well. It has the following desired properties * It is monotonically increasing with distance, i.e. attracting. * For large ''A'', it is approximately flat in the center. * Nucleons near the surface of the nucleus (i.e. having ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Woods Saxon Potential2
Woods or The Woods may refer to: Common meanings * Woodland * Forest * Wood, solid material from trees or shrubs Places United States * Woods, Kentucky * Woods, Oregon * Woods, a municipality in Liberty County, Florida * The Woods, a neighborhood in Shenandoah, Louisiana Elsewhere * Woods, Ontario, an area of Carling, Ontario, Canada * Woods, South Australia, an area of Owen * The Woods, a locality in Sandwell, England Culture Film * ''The Woods'' (2006 film), a film directed by Lucky McKee * ''The Woods'' (2011 film), a film directed by Matthew Lessner * ''The Woods'', a false working title used for the 2016 film ''Blair Witch'' (film) Music * ''The Woods'' (album), 2005 album by Sleater-Kinney * Woods (band), American folk-rock band from New York * "Woods", a song by Fireworks from their album ''Oh, Common Life'', 2014 * "Woods", a song by Mac Miller from his album '' Circles'', 2020 Other uses in culture * ''The Woods'', 2007 novel by Harlan Coben ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuclear Physics
Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter. Nuclear physics should not be confused with atomic physics, which studies the atom as a whole, including its electrons. Discoveries in nuclear physics have led to applications in many fields. This includes nuclear power, nuclear weapons, nuclear medicine and magnetic resonance imaging, industrial and agricultural isotopes, ion implantation in materials engineering, and radiocarbon dating in geology and archaeology. Such applications are studied in the field of nuclear engineering. Particle physics evolved out of nuclear physics and the two fields are typically taught in close association. Nuclear astrophysics, the application of nuclear physics to astrophysics, is crucial in explaining the inner workings of stars and the origin of the chemical elements. History The history of nuclear physics as a di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Review
''Physical Review'' is a peer-reviewed scientific journal established in 1893 by Edward Nichols. It publishes original research as well as scientific and literature reviews on all aspects of physics. It is published by the American Physical Society (APS). The journal is in its third series, and is split in several sub-journals each covering a particular field of physics. It has a sister journal, ''Physical Review Letters'', which publishes shorter articles of broader interest. History ''Physical Review'' commenced publication in July 1893, organized by Cornell University professor Edward Nichols and helped by the new president of Cornell, J. Gould Schurman. The journal was managed and edited at Cornell in upstate New York from 1893 to 1913 by Nichols, Ernest Merritt, and Frederick Bedell. The 33 volumes published during this time constitute ''Physical Review Series I''. The American Physical Society (APS), founded in 1899, took over its publication in 1913 and star ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
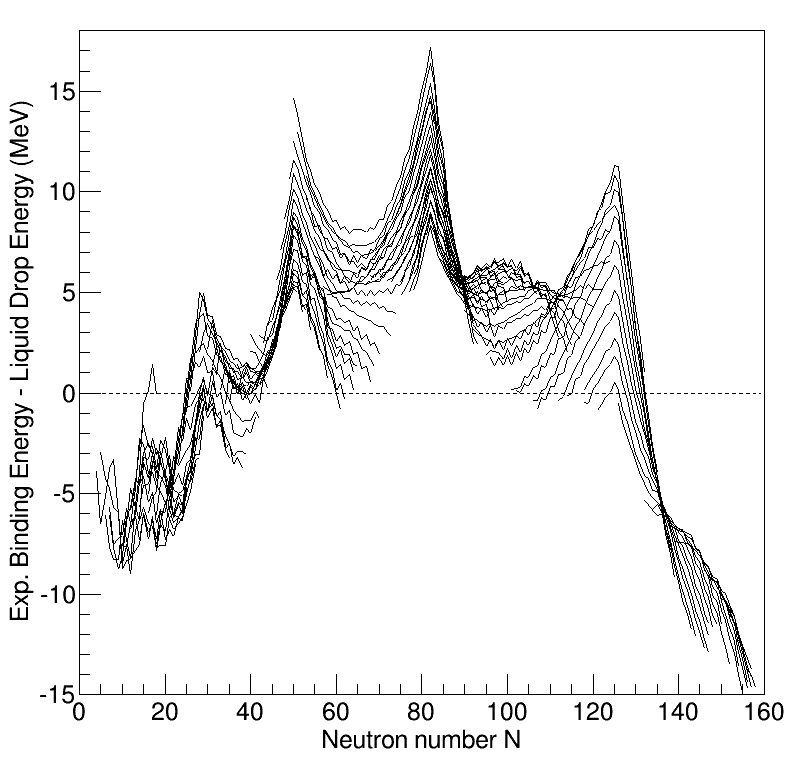
Nuclear Shell Model
In nuclear physics, atomic physics, and nuclear chemistry, the nuclear shell model is a model of the atomic nucleus which uses the Pauli exclusion principle to describe the structure of the nucleus in terms of energy levels. The first shell model was proposed by Dmitri Ivanenko (together with E. Gapon) in 1932. The model was developed in 1949 following independent work by several physicists, most notably Eugene Paul Wigner, Maria Goeppert Mayer and J. Hans D. Jensen, who shared the 1963 Nobel Prize in Physics for their contributions. The nuclear shell model is partly analogous to the atomic shell model, which describes the arrangement of electrons in an atom in that filled shell results in better stability. When adding nucleons ( protons or neutrons) to a nucleus, there are certain points where the binding energy of the next nucleon is significantly less than the last one. This observation that there are specific magic quantum numbers of nucleons (2, 8, 20, 28, 50, 82, 126 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuclear Structure
Understanding the structure of the atomic nucleus is one of the central challenges in nuclear physics. Models The liquid drop model The liquid drop model is one of the first models of nuclear structure, proposed by Carl Friedrich von Weizsäcker in 1935. It describes the nucleus as a semiclassical fluid made up of neutrons and protons, with an internal repulsive electrostatic force proportional to the number of protons. The quantum mechanical nature of these particles appears via the Pauli exclusion principle, which states that no two nucleons of the same kind can be at the same state. Thus the fluid is actually what is known as a Fermi liquid. In this model, the binding energy of a nucleus with Z protons and N neutrons is given by :E_ = a_ A - a_ A^ - a_ \frac - a_ \frac - \delta(A,Z) where A=Z+N is the total number of nucleons ( Mass Number). The terms proportional to A and A^ represent the volume and surface energy of the liquid drop, the term proportional to Z^ repre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuclear Force
The nuclear force (or nucleon–nucleon interaction, residual strong force, or, historically, strong nuclear force) is a force that acts between the protons and neutrons of atoms. Neutrons and protons, both nucleons, are affected by the nuclear force almost identically. Since protons have charge +1 ''e'', they experience an electric force that tends to push them apart, but at short range the attractive nuclear force is strong enough to overcome the electromagnetic force. The nuclear force binds nucleons into atomic nuclei. The nuclear force is powerfully attractive between nucleons at distances of about 0.8 femtometre (fm, or 0.8×10−15 metre), but it rapidly decreases to insignificance at distances beyond about 2.5 fm. At distances less than 0.7 fm, the nuclear force becomes repulsive. This repulsion is responsible for the size of nuclei, since nucleons can come no closer than the force allows. (The size of an atom, measured in angstroms (Å, or 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yukawa Potential
In particle, atomic and condensed matter physics, a Yukawa potential (also called a screened Coulomb potential) is a potential named after the Japanese physicist Hideki Yukawa. The potential is of the form: :V_\text(r)= -g^2\frac, where is a magnitude scaling constant, i.e. is the amplitude of potential, is the mass of the particle, is the radial distance to the particle, and is another scaling constant, so that r \approx \tfrac is the approximate range. The potential is monotonically increasing in and it is negative, implying the force is attractive. In the SI system, the unit of the Yukawa potential is (1/meters). The Coulomb potential of electromagnetism is an example of a Yukawa potential with the e^ factor equal to 1, everywhere. This can be interpreted as saying that the photon mass is equal to 0. The photon is the force-carrier between interacting, charged particles. In interactions between a meson field and a fermion field, the constant is equal to the gauge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle In A Box
In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example, a particle trapped inside a large box can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never "sit still". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes. The particle in a box mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Harmonic Oscillator
量子調和振動子 は、調和振動子, 古典調和振動子 の 量子力学, 量子力学 類似物です。任意の滑らかな ポテンシャル エネルギー, ポテンシャル は通常、安定した 平衡点 の近くで 調和振動子#単純調和振動子, 調和ポテンシャル として近似できるため、最も量子力学における重要なモデル系。さらに、これは正確な量子力学システムのリスト, 解析解法が知られている数少ない量子力学系の1つである。 author=Griffiths, David J. , title=量子力学入門 , エディション=2nd , 出版社=プレンティス・ホール , 年=2004 , isbn=978-0-13-805326-0 , author-link=David Griffiths (物理学者) , URL アクセス = 登録 , url=https://archive.org/details/introductiontoel00grif_0 One-dimensional harmonic oscillator Hamiltonian and energy eigenstates 粒子の ハミルトニアン (量子力学), ハミルトニアン は次の� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Potential Well
The finite potential well (also known as the finite square well) is a concept from quantum mechanics. It is an extension of the infinite potential well, in which a particle is confined to a "box", but one which has finite potential "walls". Unlike the infinite potential well, there is a probability associated with the particle being found outside the box. The quantum mechanical interpretation is unlike the classical interpretation, where if the total energy of the particle is less than the potential energy barrier of the walls it cannot be found outside the box. In the quantum interpretation, there is a non-zero probability of the particle being outside the box even when the energy of the particle is less than the potential energy barrier of the walls (cf quantum tunnelling). Particle in a 1-dimensional box For the 1-dimensional case on the ''x''-axis, the time-independent Schrödinger equation can be written as: where *\hbar = \frac is the reduced Planck's constant, *h is P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Nuclear Force
The strong interaction or strong force is a fundamental interaction that confines quarks into proton, neutron, and other hadron particles. The strong interaction also binds neutrons and protons to create atomic nuclei, where it is called the nuclear force. Most of the mass of a common proton or neutron is the result of the strong interaction energy; the individual quarks provide only about 1% of the mass of a proton. At the range of 10−15 m (slightly more than the radius of a nucleon), the strong force is approximately 100 times as strong as electromagnetism, 106 times as strong as the weak interaction, and 1038 times as strong as gravitation. The strong interaction is observable at two ranges and mediated by two force carriers. On a larger scale (of about 1 to 3 fm), it is the force (carried by mesons) that binds protons and neutrons (nucleons) together to form the nucleus of an atom. On the smaller scale (less than about 0.8 fm, the radius of a nuc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |