|
Womersley Number
The Womersley number (\alpha or \text) is a dimensionless number in biofluid mechanics and biofluid dynamics. It is a dimensionless expression of the pulsatile flow frequency in relation to viscous effects. It is named after John R. Womersley (1907–1958) for his work with blood flow in arteries. The Womersley number is important in keeping dynamic similarity when scaling an experiment. An example of this is scaling up the vascular system for experimental study. The Womersley number is also important in determining the thickness of the boundary layer to see if entrance effects can be ignored. This square root of this number is also referred to as Stokes number, \text=\sqrt, due to the pioneering work done by Sir George Stokes on the Stokes second problem. Derivation The Womersley number, usually denoted \alpha, is defined by the relation \alpha^2 = \frac = \frac = \frac = \frac \, , where L is an appropriate length scale (for example the radius of a pipe), \omega is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Number
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1), ISBN 978-92-822-2272-0. which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time (measured in seconds). Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians. History Quantities having dimension one, ''dimensionless quantities'', regularly occur in sciences, and are formally treated within the field of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematic Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties is n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biomechanics
Biomechanics is the study of the structure, function and motion of the mechanical aspects of biological systems, at any level from whole organisms to organs, cells and cell organelles, using the methods of mechanics. Biomechanics is a branch of biophysics. In 2022, computational mechanics goes far beyond pure mechanics, and involves other physical actions: chemistry, heat and mass transfer, electric and magnetic stimuli and many others. Etymology The word "biomechanics" (1899) and the related "biomechanical" (1856) come from the Ancient Greek βίος ''bios'' "life" and μηχανική, ''mēchanikē'' "mechanics", to refer to the study of the mechanical principles of living organisms, particularly their movement and structure. Subfields Biofluid mechanics Biological fluid mechanics, or biofluid mechanics, is the study of both gas and liquid fluid flows in or around biological organisms. An often studied liquid biofluid problem is that of blood flow in the human card ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, if the radius of a filled sphere i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
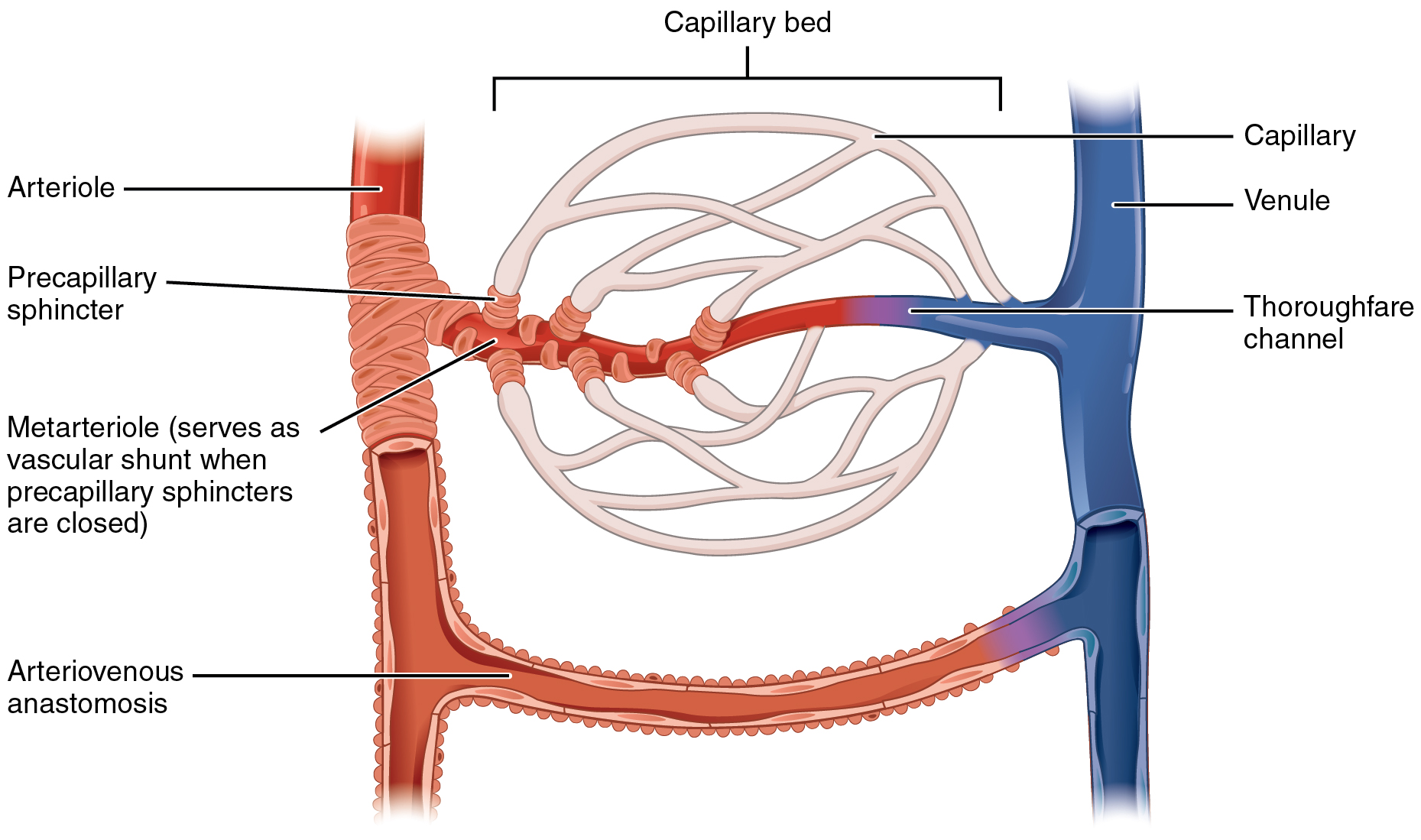
Microcirculation
The microcirculation is the circulation of the blood in the smallest blood vessels, the microvessels of the microvasculature present within organ tissues. The microvessels include terminal arterioles, metarterioles, capillaries, and venules. Arterioles carry oxygenated blood to the capillaries, and blood flows out of the capillaries through venules into veins. In addition to these blood vessels, the microcirculation also includes lymphatic capillaries and collecting ducts. The main functions of the microcirculation are the delivery of oxygen and nutrients and the removal of carbon dioxide (CO2). It also serves to regulate blood flow and tissue perfusion thereby affecting blood pressure and responses to inflammation which can include edema (swelling). Most vessels of the microcirculation are lined by flattened cells of the endothelium and many of them are surrounded by contractile cells called pericytes. The endothelium provides a smooth surface for the flow of blood and regul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes Number
The Stokes number (Stk), named after George Gabriel Stokes, is a dimensionless number characterising the behavior of particles suspended in a fluid flow. The Stokes number is defined as the ratio of the characteristic time of a particle (or droplet) to a characteristic time of the flow or of an obstacle, or :\mathrm = \frac where t_0 is the relaxation time of the particle (the time constant in the exponential decay of the particle velocity due to drag), u_0 is the fluid velocity of the flow well away from the obstacle and l_0 is the characteristic dimension of the obstacle (typically its diameter). A particle with a low Stokes number follows fluid streamlines (perfect advection), while a particle with a large Stokes number is dominated by its inertia and continues along its initial trajectory. In the case of Stokes flow, which is when the particle (or droplet) Reynolds number is less than unity, the particle drag coefficient is inversely proportional to the Reynolds number i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Navier–Stokes Equations
In physics, the Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes). The Navier–Stokes equations mathematically express conservation of momentum and conservation of mass for Newtonian fluids. They are sometimes accompanied by an equation of state relating pressure, temperature and density. They arise from applying Isaac Newton's second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term (proportional to the gradient of velocity) and a pressure term—hence describing ''viscous flow''. The difference between them and the closely related Euler equations is that Navier–Stokes equations take ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strouhal Number
In dimensional analysis, the Strouhal number (St, or sometimes Sr to avoid the conflict with the Stanton number) is a dimensionless number describing oscillating flow mechanisms. The parameter is named after Vincenc Strouhal, a Czech physicist who experimented in 1878 with wires experiencing vortex shedding and singing in the wind. The Strouhal number is an integral part of the fundamentals of fluid mechanics. The Strouhal number is often given as \text = \frac, where ''f'' is the frequency of vortex shedding, ''L'' is the characteristic length (for example, hydraulic diameter or the airfoil thickness) and ''U'' is the flow velocity. In certain cases, like heaving (plunging) flight, this characteristic length is the amplitude of oscillation. This selection of characteristic length can be used to present a distinction between Strouhal number and reduced frequency: \text = \frac, where ''k'' is the reduced frequency, and ''A'' is amplitude of the heaving oscillation. Fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow ( eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Length
In physics, a characteristic length is an important dimension that defines the scale of a physical system. Often, such a length is used as an input to a formula in order to predict some characteristics of the system, and it is usually required by the construction of a dimensionless quantity, in the general framework of dimensional analysis In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their base quantities (such as length, mass, time, and electric current) and units of measure (such as m ... and in particular applications such as fluid mechanics. In computational mechanics, a characteristic length is defined to force localization of a stress softening constitutive equation. The length is associated with an integration point. For 2D analysis, it is calculated by taking the square root of the area. For 3D analysis, it is calculated by taking the cubic root of the volume associated to th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties is n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)