|
Wiener Filter
In signal processing, the Wiener filter is a filter used to produce an estimate of a desired or target random process by linear time-invariant ( LTI) filtering of an observed noisy process, assuming known stationary signal and noise spectra, and additive noise. The Wiener filter minimizes the mean square error between the estimated random process and the desired process. Description The goal of the Wiener filter is to compute a statistical estimate of an unknown signal using a related signal as an input and filtering that known signal to produce the estimate as an output. For example, the known signal might consist of an unknown signal of interest that has been corrupted by additive noise. The Wiener filter can be used to filter out the noise from the corrupted signal to provide an estimate of the underlying signal of interest. The Wiener filter is based on a statistical approach, and a more statistical account of the theory is given in the minimum mean square error (MMSE) e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
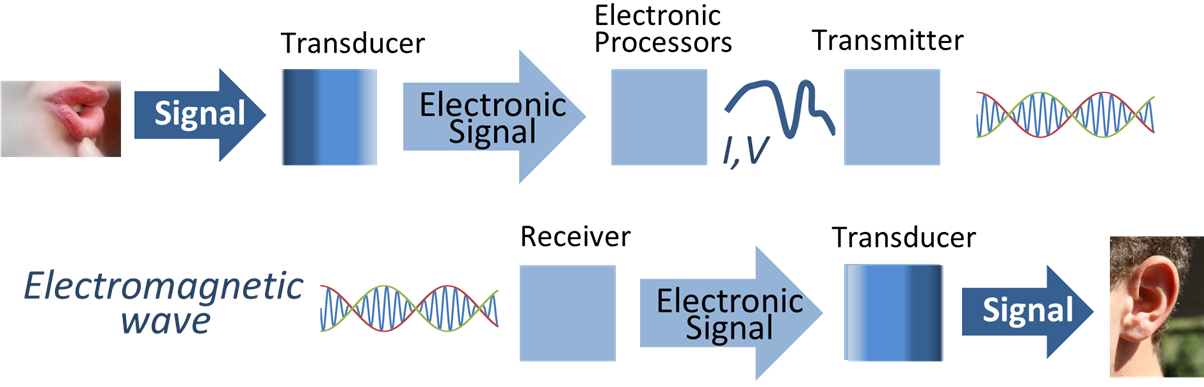
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Causal System
In control theory, a causal system (also known as a physical or nonanticipative system) is a system where the output depends on past and current inputs but not future inputs—i.e., the output y(t_) depends only on the input x(t) for values of t \le t_. The idea that the output of a function at any time depends only on past and present values of input is defined by the property commonly referred to as causality. A system that has ''some'' dependence on input values from the future (in addition to possible dependence on past or current input values) is termed a non-causal or acausal system, and a system that depends ''solely'' on future input values is an anticausal system. Note that some authors have defined an anticausal system as one that depends solely on future ''and present'' input values or, more simply, as a system that does not depend on past input values. Classically, nature or physical reality has been considered to be a causal system. Physics involving special relat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levinson Recursion
Levinson recursion or Levinson–Durbin recursion is a procedure in linear algebra to recursively calculate the solution to an equation involving a Toeplitz matrix. The algorithm runs in time, which is a strong improvement over Gauss–Jordan elimination, which runs in Θ(''n''3). The Levinson–Durbin algorithm was proposed first by Norman Levinson in 1947, improved by James Durbin in 1960, and subsequently improved to and then multiplications by W. F. Trench and S. Zohar, respectively. Other methods to process data include Schur decomposition and Cholesky decomposition. In comparison to these, Levinson recursion (particularly split Levinson recursion) tends to be faster computationally, but more sensitive to computational inaccuracies like round-off errors. The Bareiss algorithm for Toeplitz matrices (not to be confused with the general Bareiss algorithm) runs about as fast as Levinson recursion, but it uses space, whereas Levinson recursion uses only ''O''(''n'') space. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Matrix
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, Because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if a_ denotes the entry in the ith row and jth column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero. Similarly in characteristic different from 2, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative. In linear algebra, a real symmetric matrix represents a self-adjoint operator represented in an orthonormal basis over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toeplitz Matrix
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant. For instance, the following matrix is a Toeplitz matrix: :\qquad\begin a & b & c & d & e \\ f & a & b & c & d \\ g & f & a & b & c \\ h & g & f & a & b \\ i & h & g & f & a \end. Any ''n'' × ''n'' matrix ''A'' of the form :A = \begin a_0 & a_ & a_ & \cdots & \cdots & a_ \\ a_1 & a_0 & a_ & \ddots & & \vdots \\ a_2 & a_1 & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & a_ & a_ \\ \vdots & & \ddots & a_1 & a_0 & a_ \\ a_ & \cdots & \cdots & a_2 & a_1 & a_0 \end is a Toeplitz matrix. If the ''i'', ''j'' element of ''A'' is denoted ''A''''i'', ''j'' then we have :A_ = A_ = a_. A Toeplitz matrix is not necessarily square. Solving a Toeplitz system A matrix equation of the form :Ax = b is called a Toeplitz system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermitian Matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the -th row and -th column is equal to the complex conjugate of the element in the -th row and -th column, for all indices and : or in matrix form: A \text \quad \iff \quad A = \overline . Hermitian matrices can be understood as the complex extension of real symmetric matrices. If the conjugate transpose of a matrix A is denoted by A^\mathsf, then the Hermitian property can be written concisely as Hermitian matrices are named after Charles Hermite, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of always having real eigenvalues. Other, equivalent notations in common use are A^\mathsf = A^\dagger = A^\ast, although note that in quantum mechanics, A^\ast typically means the complex conjugate only, and not the conjugate transpose. Alternative characterizations Hermit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum Mean Square Error
In statistics and signal processing, a minimum mean square error (MMSE) estimator is an estimation method which minimizes the mean square error (MSE), which is a common measure of estimator quality, of the fitted values of a dependent variable. In the Bayesian setting, the term MMSE more specifically refers to estimation with quadratic loss function. In such case, the MMSE estimator is given by the posterior mean of the parameter to be estimated. Since the posterior mean is cumbersome to calculate, the form of the MMSE estimator is usually constrained to be within a certain class of functions. Linear MMSE estimators are a popular choice since they are easy to use, easy to calculate, and very versatile. It has given rise to many popular estimators such as the Wiener–Kolmogorov filter and Kalman filter. Motivation The term MMSE more specifically refers to estimation in a Bayesian setting with quadratic cost function. The basic idea behind the Bayesian approach to estimation stems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiener Block
Wiener (from German: "Viennese") may refer to: Food * A Polish sausage (kielbasa) or "wenar" * A Vienna sausage of German origin, named after the capital of Austria * A hot dog, a cooked sausage, traditionally grilled or steamed and served in a sliced bun People * Wiener (surname) Places *Wiener Neudorf, a town in the eastern part of the Mödling district, Austria *Wiener Neustadt, a town south of Vienna, in the state of Lower Austria, Austria *Wiener Stadthalle, an indoor arena, in Vienna, Austria *Wiener Staatsoper, the Vienna State Opera Other uses *The Wiener AC, also known as Wiener AC or WAC, an Austrian sports club in Vienna * Wiener process, a mathematical model related to Brownian motion * Wiener equation, named after Norbert Wiener, assumes the current velocity of a fluid particle fluctuates randomly * Wiener filter, a noise filter used in signal processing * Wiener (crater), a crater on the far side of the Moon *''Wiener Bonbons'', a waltz by Johan Strauss II *The W ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Fraction Decomposition
In algebra, the partial fraction decomposition or partial fraction expansion of a rational fraction (that is, a fraction such that the numerator and the denominator are both polynomials) is an operation that consists of expressing the fraction as a sum of a polynomial (possibly zero) and one or several fractions with a simpler denominator. The importance of the partial fraction decomposition lies in the fact that it provides algorithms for various computations with rational functions, including the explicit computation of antiderivatives, Taylor series expansions, inverse Z-transforms, and inverse Laplace transforms. The concept was discovered independently in 1702 by both Johann Bernoulli and Gottfried Leibniz. In symbols, the ''partial fraction decomposition'' of a rational fraction of the form \frac, where and are polynomials, is its expression as \frac=p(x) + \sum_j \frac where is a polynomial, and, for each , the denominator is a power of an irreducible polynomial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiener–Hopf Method
The Wiener–Hopf method is a mathematical technique widely used in applied mathematics. It was initially developed by Norbert Wiener and Eberhard Hopf as a method to solve systems of integral equations, but has found wider use in solving two-dimensional partial differential equations with mixed boundary conditions on the same boundary. In general, the method works by exploiting the complex-analytical properties of transformed functions. Typically, the standard Fourier transform is used, but examples exist using other transforms, such as the Mellin transform. In general, the governing equations and boundary conditions are transformed and these transforms are used to define a pair of complex functions (typically denoted with '+' and '−' subscripts) which are respectively analytic in the upper and lower halves of the complex plane, and have growth no faster than polynomials in these regions. These two functions will also coincide on some region of the complex plane, typically, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform In mathematics, an integral transform maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily characterized and manipulated than in ... that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex frequency domain, also known as ''s''-domain, or s-plane). The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms ordinary differential equations into algebraic equations and convolution into multiplication. For suitable functions ''f'', the Laplace transform is the integral \mathcal\(s) = \int_0^\infty f(t)e^ \, dt. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
