|
Widom Insertion Method
The Widom insertion method is a statistical thermodynamic approach to the calculation of material and mixture properties. It is named for Benjamin Widom, who derived it in 1963.Widom, B, "Some Topics in the Theory of Fluids", ''J. Chem. Phys.'', 1963, 39(11), 2808-2812. In general, there are two theoretical approaches to determining the statistical mechanical properties of materials. The first is the direct calculation of the overall partition function of the system, which directly yields the system free energy. The second approach, known as the Widom insertion method, instead derives from calculations centering on one molecule. The Widom insertion method directly yields the chemical potential of one component rather than the system free energy. This approach is most widely applied in molecular computer simulations but has also been applied in the development of analytical statistical mechanical models. The Widom insertion method can be understood as an application of the Ja ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Thermodynamics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. This established the fields of statistical thermodynamics and statistical physics. The founding of the field of statistical mechanics is generally credited to three physicists: *Ludwig Boltzmann, who developed the fundamental interpretation of entropy in terms of a collection of microstates *James Clerk Maxwell, who developed models of probability distri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Benjamin Widom
Benjamin Widom (born 13 October 1927) is the Goldwin Smith Professor of Chemistry at Cornell University. His research interests include physical chemistry and statistical mechanics. In 1998, Widom was awarded the Boltzmann Medal "for his illuminating studies of the statistical mechanics of fluids and fluid mixtures and their interfacial properties, especially his clear and general formulation of scaling hypotheses for the equation of state and surface tensions of fluids near critical points." Academic background Widom was born in Newark, New Jersey. He graduated from New York City's Stuyvesant High School in 1945, and received his BA from Columbia University in 1949, followed by his PhD from Cornell in 1953. He became an instructor of chemistry at Cornell in 1954, was appointed assistant professor in 1955 and a full professor in 1963. He was chair of the chemistry department between 1978 and 1981. He was elected a member of the National Academy of Sciences in 1974 and a fell ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Function (statistical Mechanics)
In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless. Each partition function is constructed to represent a particular statistical ensemble (which, in turn, corresponds to a particular free energy). The most common statistical ensembles have named partition functions. The canonical partition function applies to a canonical ensemble, in which the system is allowed to exchange heat with the environment at fixed temperature, volume, and number of particles. The grand canonical partition function applies to a grand canonical ensemble, in which the system can exchange both heat a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jarzynski Equality
The Jarzynski equality (JE) is an equation in statistical mechanics that relates free energy differences between two states and the irreversible work along an ensemble of trajectories joining the same states. It is named after the physicist Christopher Jarzynski (then at the University of Washington and Los Alamos National Laboratory, currently at the University of Maryland) who derived it in 1996. Fundamentally, the Jarzynski equality points to the fact that the fluctuations in the work satisfy certain constraints separately from the average value of the work that occurs in some process. Overview In thermodynamics, the free energy difference \Delta F = F_B - F_A between two states ''A'' and ''B'' is connected to the work ''W'' done on the system through the ''inequality'': : \Delta F \leq W , with equality holding only in the case of a quasistatic process, i.e. when one takes the system from ''A'' to ''B'' infinitely slowly (such that all intermediate states are in thermody ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Activity (chemistry)
In chemical thermodynamics, activity (symbol ) is a measure of the "effective concentration" of a species in a mixture, in the sense that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution. The term "activity" in this sense was coined by the American chemist Gilbert N. Lewis in 1907. By convention, activity is treated as a dimensionless quantity, although its value depends on customary choices of standard state for the species. The activity of pure substances in condensed phases (solid or liquids) is normally taken as unity (the number 1). Activity depends on temperature, pressure and composition of the mixture, among other things. For gases, the activity is the effective partial pressure, and is usually referred to as fugacity. The difference between activity and other measures of concentration arises because the interactions between different types of molecules in non-ideal gas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, and in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating thermal noise in resistors. The Boltzmann constant has dimensions of energy divided by temperature, the same as entropy. It is named after the Austrian scientist Ludwig Boltzmann. As part of the 2019 redefinition of SI base units, the Boltzmann constant is one of the seven " defining constants" that have been given exact definitions. They are used in various combinations to define the seven SI base units. The Boltzmann constant is defined to be exactly . Roles of the Boltzmann constant Macroscopically, the ideal gas law states that, for an ideal gas, the product of pressure and volume is proportional to the product of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Factor
Factor, a Latin word meaning "who/which acts", may refer to: Commerce * Factor (agent), a person who acts for, notably a mercantile and colonial agent * Factor (Scotland), a person or firm managing a Scottish estate * Factors of production, such a factor is a resource used in the production of goods and services Science and technology Biology * Coagulation factors, substances essential for blood coagulation * Environmental factor, any abiotic or biotic factor that affects life * Enzyme, proteins that catalyze chemical reactions * Factor B, and factor D, peptides involved in the alternate pathway of immune system complement activation * Transcription factor, a protein that binds to specific DNA sequences Computer science and information technology * Factor (programming language), a concatenative stack-oriented programming language * Factor (Unix), a utility for factoring an integer into its prime factors * Factor, a substring, a subsequence of consecutive symbols in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
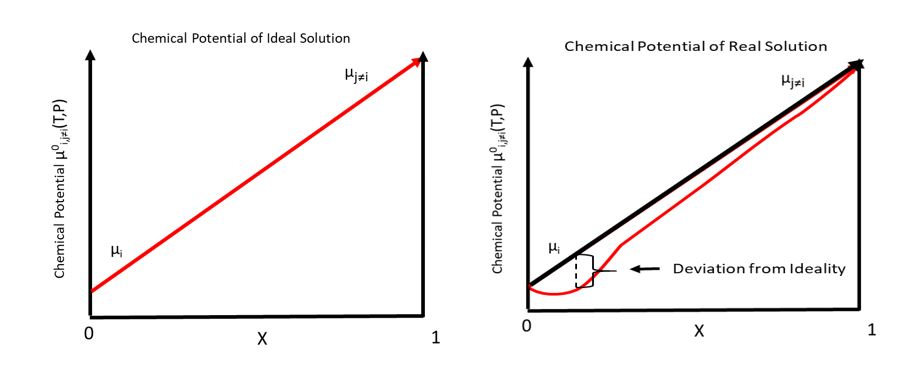
Chemical Potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of State
In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate for weakly polar gases at low pressures and moderate temperatures. This equation becomes increasingly inaccurate at higher pressures and lower temperatures, and fails to predi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressibility Factor
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behaviour.Properties of Natural Gases . Includes a chart of compressibility factors versus reduced pressure and reduced temperature (on last page of the PDF document) In general, deviation from ideal behaviour becomes more significant the closer a gas is to a phase change, the lower the temperat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Field Theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random ( stochastic) models by studying a simpler model that approximates the original by averaging over degrees of freedom (the number of values in the final calculation of a statistic that are free to vary). Such models consider many individual components that interact with each other. The main idea of MFT is to replace all interactions to any one body with an average or effective interaction, sometimes called a ''molecular field''. This reduces any many-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a lower computational cost. MFT has since been applied to a wide range of fields outside of physics, including statistical inference, graphical models, neuroscience, artificial intelligence, epidemic models, queueing theory, computer-netwo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |