|
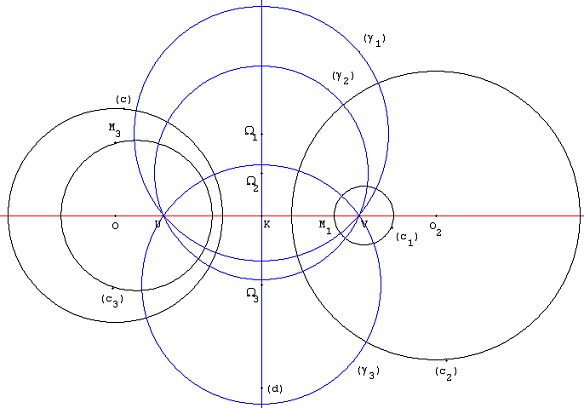
W-curve
In geometry, a W-curve is a curve in projective ''n''-space that is invariant under a 1-parameter group of projective transformations. W-curves were first investigated by Felix Klein and Sophus Lie in 1871, who also named them. W-curves in the real projective plane can be constructed with straightedge alone. Many well-known curves are W-curves, among them conics, logarithmic spirals, powers (like ''y'' = ''x''3), logarithms and the helix, but not e.g. the sine. W-curves occur widely in the realm of plants. Name The 'W' stands for the German 'Wurf' – a ''throw'' – which in this context refers to a series of four points on a line. A 1-dimensional W-curve (read: the motion of a point on a projective line) is determined by such a series. The German "W-Kurve" sounds almost exactly like "Weg-Kurve" and the last can be translated by "path curve". That is why in the English literature one often finds "path curve" or "pathcurve". See also * Homography ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Klein
Christian Felix Klein (; 25 April 1849 – 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and group theory. His 1872 Erlangen program, classifying geometries by their basic symmetry groups, was an influential synthesis of much of the mathematics of the time. Life Felix Klein was born on 25 April 1849 in Düsseldorf, to Prussian parents. His father, Caspar Klein (1809–1889), was a Prussian government official's secretary stationed in the Rhine Province. His mother was Sophie Elise Klein (1819–1890, née Kayser). He attended the Gymnasium in Düsseldorf, then studied mathematics and physics at the University of Bonn, 1865–1866, intending to become a physicist. At that time, Julius Plücker had Bonn's professorship of mathematics and experimental physics, but by the time Klein became his assistant, in 1866, Plücker's interest wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Transformations
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation. Historically, homographies (and projective spaces) have been introduced to study perspective and projections in Euclidean geometry, and the term ''homography'', which, etymologically, roughly means "similar drawing", dates from this time. At the end of the 19th century, formal definitions of projective spaces were introduced, which differed from extending Euclidean or affine spaces by adding points at infinity. The term "projective transformation" originated in these abstract ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sophus Lie
Marius Sophus Lie ( ; ; 17 December 1842 – 18 February 1899) was a Norwegian mathematician. He largely created the theory of continuous symmetry and applied it to the study of geometry and differential equations. Life and career Marius Sophus Lie was born on 17 December 1842 in the small town of Nordfjordeid. He was the youngest of six children born to a Lutheran pastor named Johann Herman Lie, and his wife who came from a well-known Trondheim family. He had his primary education in the south-eastern coast of Moss, before attending high school at Oslo (known then as Christiania). After graduating from high school, his ambition towards a military career was dashed when the army rejected him due to his poor eyesight. It was then that he decided to enrol at the University of Christiania. Sophus Lie's first mathematical work, ''Repräsentation der Imaginären der Plangeometrie'', was published in 1869 by the Academy of Sciences in Christiania and also by ''Crelle's Journal''. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Georg Scheffers
250px Georg Scheffers (21 November 1866 – 12 August 1945) was a German mathematician specializing in differential geometry. Life Scheffers was born on 21 November 1866 in the village of Altendorf near Holzminden (today incorporated into Holzminden). Scheffers began his university career at the University of Leipzig where he studied with Felix Klein and Sophus Lie. Scheffers was a coauthor with Lie for three of the earliest expressions of Lie theory: * ''Lectures on Differential equations with known Infinitesimal transformations'' (1893), * ''Lectures on Continuous groups'' (1893), and * ''Geometry of Contact Transformations'' (1896). All three are now available online through archive.org. In 1896 Scheffers became docent at the Technical University of Darmstadt, where he was raised to professor in 1900. From 1907 to 1935, when he retired, Scheffers was a professor at the Technical University of Berlin. In 1901–1902 he published a famous two-volume textbook entitled ''Anw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homography
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation. Historically, homographies (and projective spaces) have been introduced to study perspective and projections in Euclidean geometry, and the term ''homography'', which, etymologically, roughly means "similar drawing", dates from this time. At the end of the 19th century, formal definitions of projective spaces were introduced, which differed from extending Euclidean or affine spaces by adding points at infinity. The term "projective transformation" originated in these abstra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore, other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, ''point'' and ''line'' are primitive entities that are related by the incidence relation "a point is on a line" or "a line passes through a point", which is subject to the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from the fol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helix
A helix () is a shape like a corkscrew or spiral staircase. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is formed as two intertwined helices, and many proteins have helical substructures, known as alpha helices. The word ''helix'' comes from the Greek word ''ἕλιξ'', "twisted, curved". A "filled-in" helix – for example, a "spiral" (helical) ramp – is a surface called ''helicoid''. Properties and types The ''pitch'' of a helix is the height of one complete helix turn, measured parallel to the axis of the helix. A double helix consists of two (typically congruent) helices with the same axis, differing by a translation along the axis. A circular helix (i.e. one with constant radius) has constant band curvature and constant torsion. A ''conic helix'', also known as a ''conic spiral'', may be defined as a spiral on a conic surface, with the distance to the apex an expo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klein's Encyclopedia
Felix Klein's ''Encyclopedia of Mathematical Sciences'' is a German mathematical Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ... encyclopedia published in six volumes from 1898 to 1933. Klein and Wilhelm Franz Meyer were organizers of the encyclopedia. Its full title in English is ''Encyclopedia of Mathematical Sciences Including Their Applications'', which is ''Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen'' (EMW). It is 20,000 pages in length (6 volumes, ''i.e. Bände'', published in 23 separate books, 1-1, 1-2, 2-1-1, 2-1-2, 2-2, 2-3-1, 2-3-2, 3-1-1, 3-1-2, 3-2-1, 3-2-2a, 3-2-2b, 3-3, 4-1, 4-2, 4-3, 4-4, 5-1, 5-2, 5-3, 6-1, 6-2-1, 6-2-2) and was published by B.G. Teubner Verlag, publisher of ''Mathematische Annalen''. Today, Göttinger Digit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted simply as \sin \theta and \cos \theta. More generally, the definitions of sine and cosine can be extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and lig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Spiral
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral curve that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer (1525) who called it an "eternal line" ("ewige Linie"). More than a century later, the curve was discussed by Descartes (1638), and later extensively investigated by Jacob Bernoulli, who called it ''Spira mirabilis'', "the marvelous spiral". The logarithmic spiral can be distinguished from the Archimedean spiral by the fact that the distances between the turnings of a logarithmic spiral increase in geometric progression, while in an Archimedean spiral these distances are constant. Definition In polar coordinates (r, \varphi) the logarithmic spiral can be written as r = ae^,\quad \varphi \in \R, or \varphi = \frac \ln \frac, with e being the base of natural logarithms, and a > 0, k\ne 0 being real constants. In Cartesian coordinates The logarithmic spiral with the polar equation r = a e^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of is , or . The logarithm of to ''base'' is denoted as , or without parentheses, , or even without the explicit base, , when no confusion is possible, or when the base does not matter such as in big O notation. The logarithm base is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number as its base; its use is widespread in mathematics and physics, because of its very simple derivative. The binary logarithm uses base and is frequently used in computer science. Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. They were rapidly adopted by navigators, scientists, engineers, surveyors and others to perform high-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |