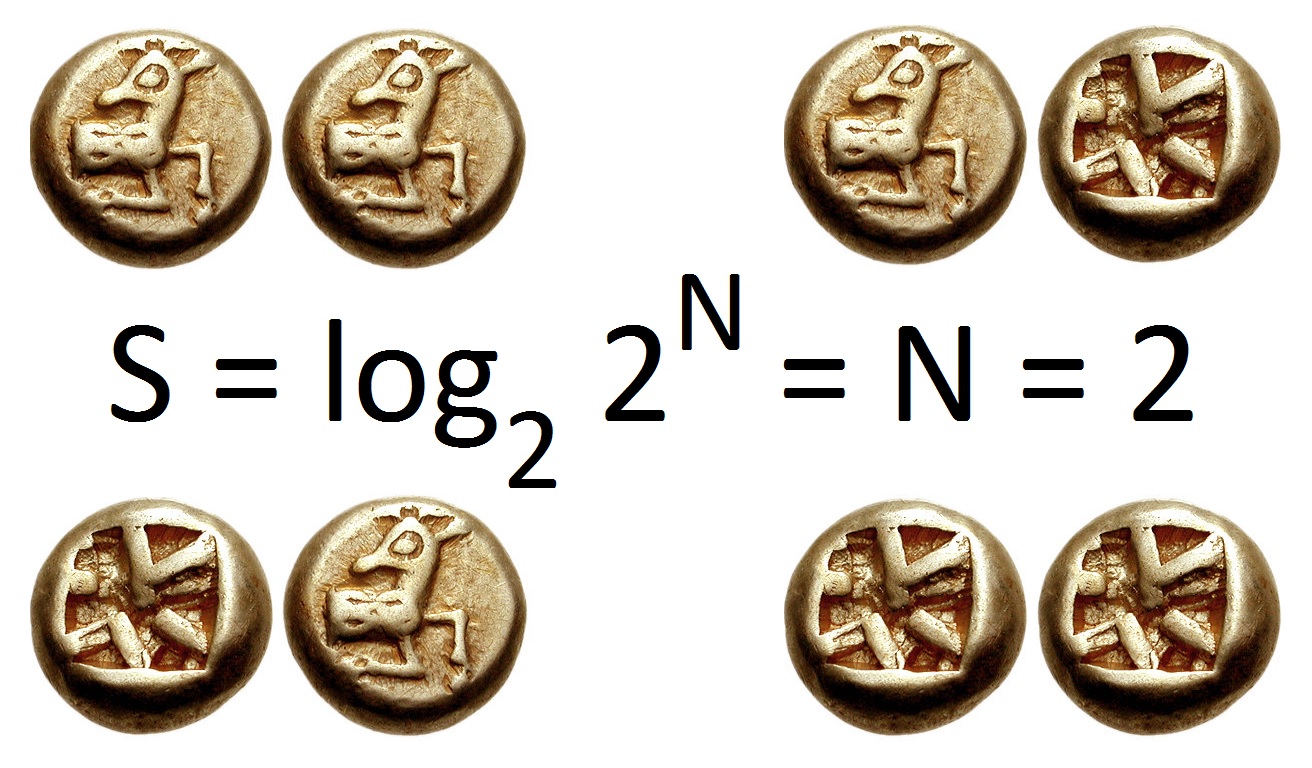|
Variational Bayesian Methods
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables (usually termed "data") as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes: #To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables. #To derive a lower bound for the marginal likelihood (sometimes called the ''evidence'') of the observed data (i.e. the marginal probability of the data given the model, with marginalization performed over unobserved v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ..., an integral assigns numbers to functions in a way that describes Displacement (geometry), displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with Derivative, differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
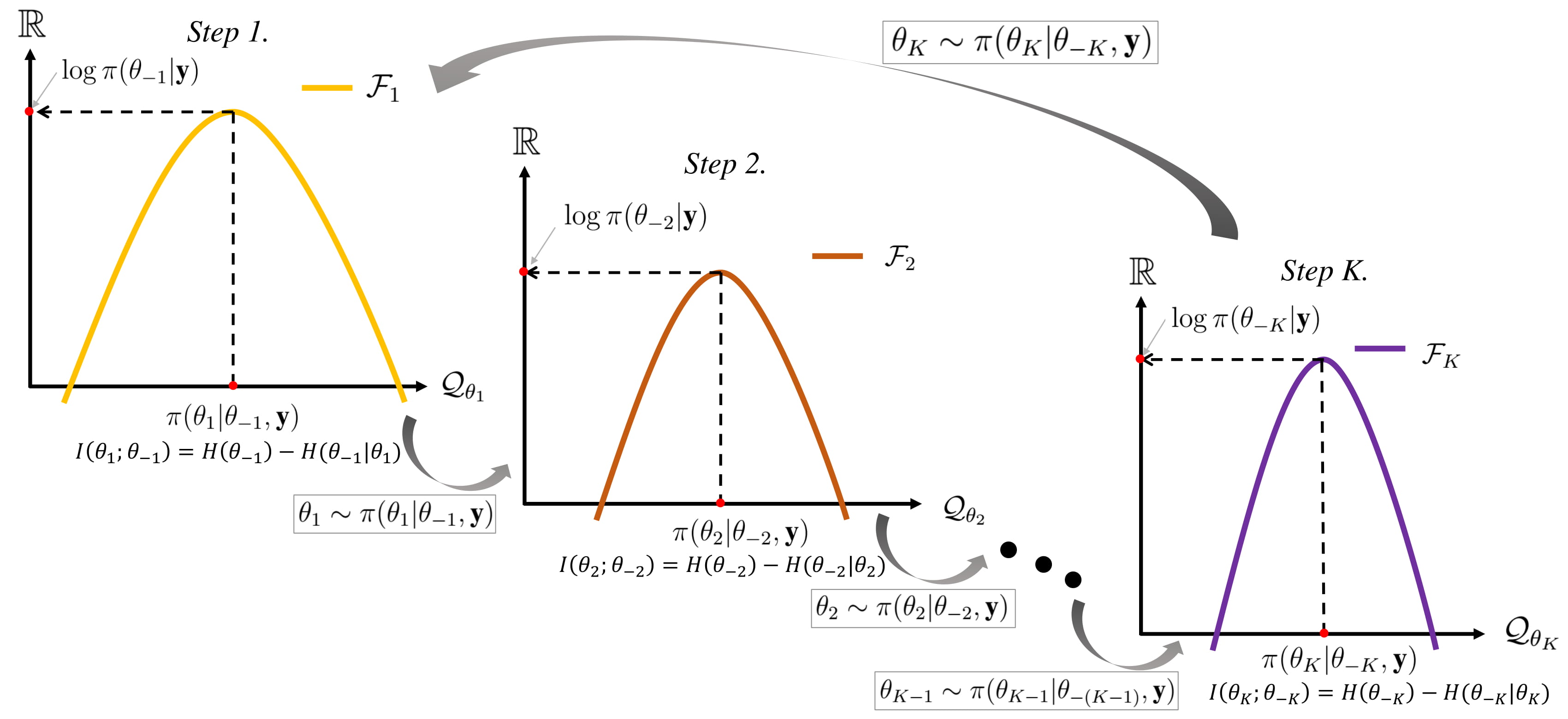
Gibbs Sampling
In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for obtaining a sequence of observations which are approximated from a specified multivariate probability distribution, when direct sampling is difficult. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes use of random numbers), and is an alternative to deterministic algorithms for statistical inferenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to, 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper "A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Free Energy
The thermodynamic free energy is a concept useful in the thermodynamics of chemical or thermal processes in engineering and science. The change in the free energy is the maximum amount of work that a thermodynamic system can perform in a process at constant temperature, and its sign indicates whether the process is thermodynamically favorable or forbidden. Since free energy usually contains potential energy, it is not absolute but depends on the choice of a zero point. Therefore, only relative free energy values, or changes in free energy, are physically meaningful. The free energy is a thermodynamic state function, like the internal energy, enthalpy, and entropy. The free energy is the portion of any first-law energy that is available to perform thermodynamic work at constant temperature, ''i.e.'', work mediated by thermal energy. Free energy is subject to irreversible loss in the course of such work. Since first-law energy is always conserved, it is evident that free energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Evidence
A marginal likelihood is a likelihood function that has been integrated over the parameter space. In Bayesian statistics, it represents the probability of generating the observed sample from a prior and is therefore often referred to as model evidence or simply evidence. Concept Given a set of independent identically distributed data points \mathbf=(x_1,\ldots,x_n), where x_i \sim p(x, \theta) according to some probability distribution parameterized by \theta, where \theta itself is a random variable described by a distribution, i.e. \theta \sim p(\theta\mid\alpha), the marginal likelihood in general asks what the probability p(\mathbf\mid\alpha) is, where \theta has been marginalized out (integrated out): :p(\mathbf\mid\alpha) = \int_\theta p(\mathbf\mid\theta) \, p(\theta\mid\alpha)\ \operatorname\!\theta The above definition is phrased in the context of Bayesian statistics in which case p(\theta\mid\alpha) is called prior density and p(\mathbf\mid\theta) is the likelihood. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to end th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expectation Propagation
Expectation propagation (EP) is a technique in Bayesian machine learning. EP finds approximations to a probability distribution. It uses an iterative approach that uses the factorization structure of the target distribution. It differs from other Bayesian approximation approaches such as variational Bayesian methods. More specifically, suppose we wish to approximate an intractable probability distribution p(\mathbf) with a tractable distribution q(\mathbf). Expectation propagation achieves this approximation by minimizing the Kullback-Leibler divergence \mathrm(p, , q). Variational Bayesian methods minimize \mathrm(q, , p) instead. If q(\mathbf) is a Gaussian \mathcal(\mathbf, \mu, \Sigma), then \mathrm(p, , q) is minimized with \mu and \Sigma being equal to the mean of p(\mathbf) and the covariance of p(\mathbf), respectively; this is called moment matching. Applications Expectation propagation via moment matching plays a vital role in approximation for indicator functions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
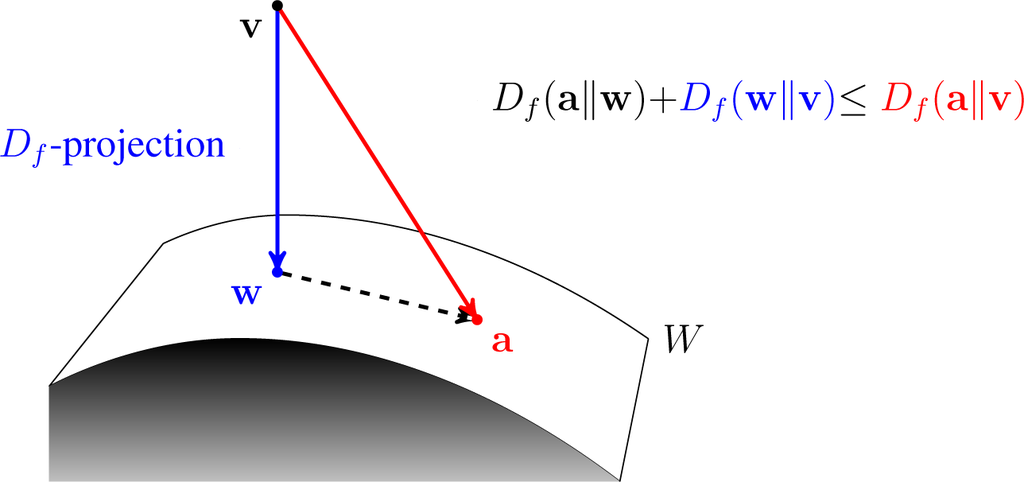
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how one probability distribution ''P'' is different from a second, reference probability distribution ''Q''. A simple interpretation of the KL divergence of ''P'' from ''Q'' is the expected excess surprise from using ''Q'' as a model when the actual distribution is ''P''. While it is a distance, it is not a metric, the most familiar type of distance: it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for certain classes of distributions (notably an exponential family), it satisfies a generalized Pythagorean theorem (which applies to squared distances). In the simple case, a relative entropy of 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus Of Variations
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as ''geodesics''. A related problem is posed by Fermat's principle: light follows the path of shortest optical length connecting two points, which depends up ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Posterior Distribution
The posterior probability is a type of conditional probability that results from updating the prior probability with information summarized by the likelihood via an application of Bayes' rule. From an epistemological perspective, the posterior probability contains everything there is to know about an uncertain proposition (such as a scientific hypothesis, or parameter values), given prior knowledge and a mathematical model describing the observations available at a particular time. After the arrival of new information, the current posterior probability may serve as the prior in another round of Bayesian updating. In the context of Bayesian statistics, the posterior probability distribution usually describes the epistemic uncertainty about statistical parameters conditional on a collection of observed data. From a given posterior distribution, various point and interval estimates can be derived, such as the maximum a posteriori (MAP) or the highest posterior density interval (HPD ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum A Posteriori Estimation
In Bayesian statistics, a maximum a posteriori probability (MAP) estimate is an estimate of an unknown quantity, that equals the mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data. It is closely related to the method of maximum likelihood (ML) estimation, but employs an augmented optimization objective which incorporates a prior distribution (that quantifies the additional information available through prior knowledge of a related event) over the quantity one wants to estimate. MAP estimation can therefore be seen as a regularization of maximum likelihood estimation. Description Assume that we want to estimate an unobserved population parameter \theta on the basis of observations x. Let f be the sampling distribution of x, so that f(x\mid\theta) is the probability of x when the underlying population parameter is \theta. Then the function: :\theta \mapsto f(x \mid \theta) \! is known as th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |