|
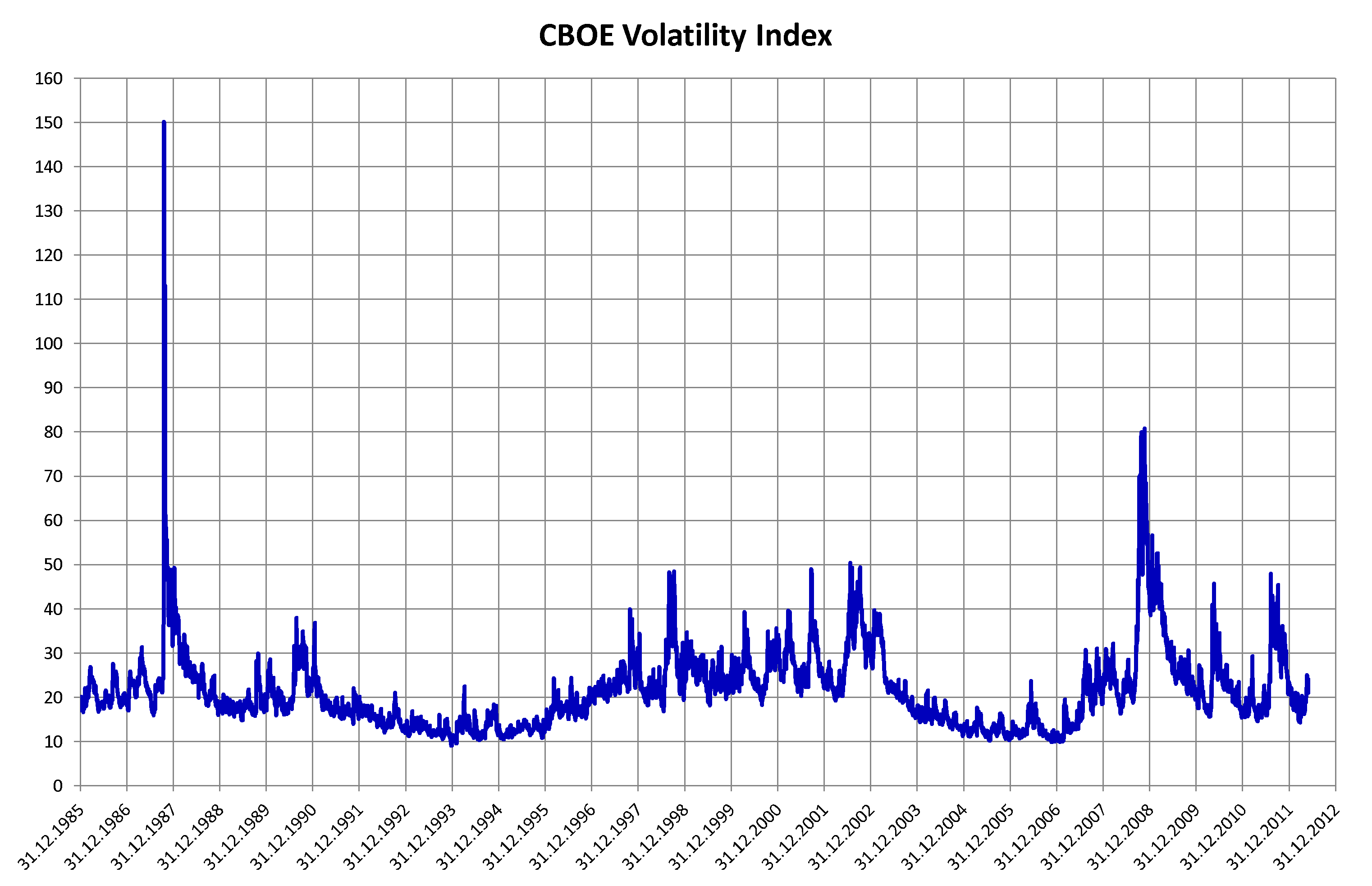
Volatility Clustering
In finance, volatility clustering refers to the observation, first noted by Mandelbrot (1963), that "large changes tend to be followed by large changes, of either sign, and small changes tend to be followed by small changes." A quantitative manifestation of this fact is that, while returns themselves are uncorrelated, absolute returns , r_, or their squares display a positive, significant and slowly decaying autocorrelation function: corr(, r, , , r , ) > 0 for τ ranging from a few minutes to several weeks. This empirical property has been documented in the 90's by Granger and Ding (1993) and Ding and Granger (1996) among others; see also. Some studies point further to long-range dependence in volatility time series, see Ding, Granger and Engle (1993) and Barndorff-Nielsen and Shephard. Observations of this type in financial time series go against simple random walk models and have led to the use of GARCH models and mean-reverting stochastic volatility models in financial fore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finance
Finance is the study and discipline of money, currency and capital assets. It is related to, but not synonymous with economics, the study of production, distribution, and consumption of money, assets, goods and services (the discipline of financial economics bridges the two). Finance activities take place in financial systems at various scopes, thus the field can be roughly divided into personal, corporate, and public finance. In a financial system, assets are bought, sold, or traded as financial instruments, such as currencies, loans, bonds, shares, stocks, options, futures, etc. Assets can also be banked, invested, and insured to maximize value and minimize loss. In practice, risks are always present in any financial action and entities. A broad range of subfields within finance exist due to its wide scope. Asset, money, risk and investment management aim to maximize value and minimize volatility. Financial analysis is viability, stability, and profitabili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Benoît Mandelbrot
Benoit B. Mandelbrot (20 November 1924 – 14 October 2010) was a Polish-born French-American mathematician and polymath with broad interests in the practical sciences, especially regarding what he labeled as "the art of #Fractals and the "theory of roughness", roughness" of physical phenomena and "the uncontrolled element in life". He referred to himself as a "fractalist" and is recognized for his contribution to the field of fractal geometry, which included coining the word "fractal", as well as developing a theory of "roughness and self-similarity" in nature. In 1936, at the age of 11, Mandelbrot and his family emigrated from Warsaw, Poland, to France. After World War II ended, Mandelbrot studied mathematics, graduating from universities in Paris and in the United States and receiving a master's degree in aeronautics from the California Institute of Technology. He spent most of his career in both the United States and France, having Multiple citizenship , dual French nat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clive Granger
Sir Clive William John Granger (; 4 September 1934 – 27 May 2009) was a British econometrician known for his contributions to nonlinear time series analysis. He taught in Britain, at the University of Nottingham and in the United States, at the University of California, San Diego. Granger was awarded the Nobel Memorial Prize in Economic Sciences in 2003 in recognition of the contributions that he and his co-winner, Robert F. Engle, had made to the analysis of time series data. This work fundamentally changed the way in which economists analyse financial and macroeconomic data. Biography Early life Clive Granger was born in 1934 in Swansea, south Wales, United Kingdom, to Edward John Granger and Evelyn Granger. The next year his parents moved to Lincoln. During World War II Granger and his mother moved to Cambridge because Edward joined the Royal Air Force and deployed to North Africa. Here they stayed first with Evelyn's mother, then later Edward's parents, while Clive b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert F
The name Robert is an ancient Germanic given name, from Proto-Germanic "fame" and "bright" (''Hrōþiberhtaz''). Compare Old Dutch ''Robrecht'' and Old High German ''Hrodebert'' (a compound of ''Hrōþ, Hruod'' ( non, Hróðr) "fame, glory, honour, praise, renown" and ''berht'' "bright, light, shining"). It is the second most frequently used given name of ancient Germanic origin. It is also in use Robert (surname), as a surname. Another commonly used form of the name is Rupert (name), Rupert. After becoming widely used in Continental Europe it entered England in its Old French form ''Robert'', where an Old English cognate form (''Hrēodbēorht'', ''Hrodberht'', ''Hrēodbēorð'', ''Hrœdbœrð'', ''Hrœdberð'', ''Hrōðberχtŕ'') had existed before the Norman Conquest. The feminine version is Roberta (given name), Roberta. The Italian, Portuguese, and Spanish form is Roberto (given name), Roberto. Robert is also a common name in many Germanic languages, including English ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GARCH
In econometrics, the autoregressive conditional heteroskedasticity (ARCH) model is a statistical model for time series data that describes the variance of the current error term or innovation as a function of the actual sizes of the previous time periods' error terms; often the variance is related to the squares of the previous innovations. The ARCH model is appropriate when the error variance in a time series follows an autoregressive (AR) model; if an autoregressive moving average (ARMA) model is assumed for the error variance, the model is a generalized autoregressive conditional heteroskedasticity (GARCH) model. ARCH models are commonly employed in modeling financial time series that exhibit time-varying volatility and volatility clustering, i.e. periods of swings interspersed with periods of relative calm. ARCH-type models are sometimes considered to be in the family of stochastic volatility models, although this is strictly incorrect since at time ''t'' the volatility is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Volatility
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others. Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, models based on Black-Scholes assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile and skew, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative (finance)
In finance, a derivative is a contract that ''derives'' its value from the performance of an underlying entity. This underlying entity can be an asset, Index fund, index, or interest rate, and is often simply called the "underlying". Derivatives can be used for a number of purposes, including insuring against price movements (Hedge (finance)#Etymology, hedging), increasing exposure to price movements for speculation, or getting access to otherwise hard-to-trade assets or markets. Some of the more common derivatives include Forward contract, forwards, Futures contract, futures, Option (finance), options, Swap (finance), swaps, and variations of these such as synthetic collateralized debt obligations and credit default swaps. Most derivatives are traded over-the-counter (finance), over-the-counter (off-exchange) or on an exchange such as the Chicago Mercantile Exchange, while most insurance contracts have developed into a separate industry. In the United States, after the financia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ARCH
An arch is a vertical curved structure that spans an elevated space and may or may not support the weight above it, or in case of a horizontal arch like an arch dam, the hydrostatic pressure against it. Arches may be synonymous with vaults, but a vault may be distinguished as a continuous arch forming a roof. Arches appeared as early as the 2nd millennium BC in Mesopotamian brick architecture, and their systematic use started with the ancient Romans, who were the first to apply the technique to a wide range of structures. Basic concepts An arch is a pure compression form. It can span a large area by resolving forces into compressive stresses, and thereby eliminating tensile stresses. This is sometimes denominated "arch action". As the forces in the arch are transferred to its base, the arch pushes outward at its base, denominated "thrust". As the rise, i. e. height, of the arch decreases the outward thrust increases. In order to preserve arch action and prevent coll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tim Bollerslev
Tim Peter Bollerslev (born May 11, 1958) is a Danish economist, currently the ''Juanita and Clifton Kreps Professor of Economics'' at Duke University. A fellow of the Econometric Society, Bollerslev is known for his ideas for measuring and forecasting financial market volatility and for the GARCH (generalized autoregressive conditional heteroskedasticity) model. Biography Tim Bollerslev received his MSc in economics and mathematics in 1983 from the Aarhus University in Denmark. He continued his studies in the U.S., earning his Ph.D. in 1986 from the University of California at San Diego with a thesis titled ''Generalized Autoregressive Conditional Heteroskedasticity with Applications in Finance'' written under the supervision of Robert F. Engle (Nobel Prize in Economics winner in 2003). After his graduate studies, Bollerslev taught at the Northwestern University between 1986–1995 and at the University of Virginia between 1996–1998. Since 1998 he is the Juanita and Clifton ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kurtosis
In probability theory and statistics, kurtosis (from el, κυρτός, ''kyrtos'' or ''kurtos'', meaning "curved, arching") is a measure of the "tailedness" of the probability distribution of a real-valued random variable. Like skewness, kurtosis describes a particular aspect of a probability distribution. There are different ways to quantify kurtosis for a theoretical distribution, and there are corresponding ways of estimating it using a sample from a population. Different measures of kurtosis may have different interpretations. The standard measure of a distribution's kurtosis, originating with Karl Pearson, is a scaled version of the fourth moment of the distribution. This number is related to the tails of the distribution, not its peak; hence, the sometimes-seen characterization of kurtosis as " peakedness" is incorrect. For this measure, higher kurtosis corresponds to greater extremity of deviations (or outliers), and not the configuration of data near the mean. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility (finance)
In finance, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monotonic
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if and only if it is either entirely non-increasing, or entirely non-decreasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is called ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |