|
Virginia Kiryakova
Virginia S. Kiryakova (née Virdzhinia Stoinova Hristova) is a Bulgarian mathematician known for her work on the fractional calculus, on special functions in fractional calculus including the Mittag-Leffler functions, and on the history of calculus. She is a professor in the Institute of Mathematics and Informatics of the Bulgarian Academy of Sciences. Education and career As a high school student, Kiryakova competed for Bulgaria in the 1969 International Mathematical Olympiad, earning a bronze medal. She graduated from Sofia University in 1975 with a combined bachelor's and master's degree in mathematics, and in the same year became a researcher in the Institute of Mathematics and Informatics. She earned a Ph.D. in 1987, with the thesis ''Generalized Operators of Integration and Differentiation of Fractional Order and Applications'', and completed a Dr.Sc. (habilitation) in 2010, with the thesis ''Generalized Fractional Calculus and Applications in Analysis'', supervised by Ivan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
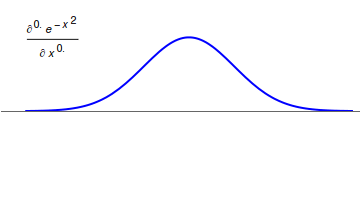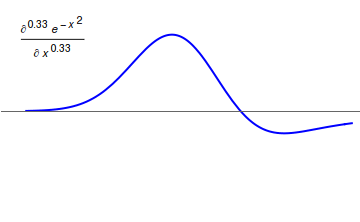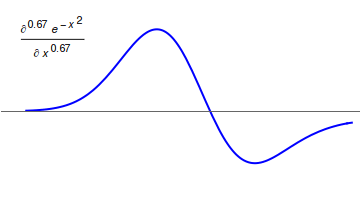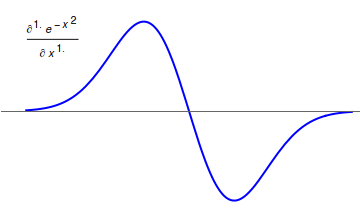
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Function
Special functions are particular mathematical functions that have more or less established names and notations due to their importance in mathematical analysis, functional analysis, geometry, physics, or other applications. The term is defined by consensus, and thus lacks a general formal definition, but the List of mathematical functions contains functions that are commonly accepted as special. Tables of special functions Many special functions appear as solutions of differential equations or integrals of elementary functions. Therefore, tables of integrals usually include descriptions of special functions, and tables of special functions include most important integrals; at least, the integral representation of special functions. Because symmetries of differential equations are essential to both physics and mathematics, the theory of special functions is closely related to the theory of Lie groups and Lie algebras, as well as certain topics in mathematical physics. Sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
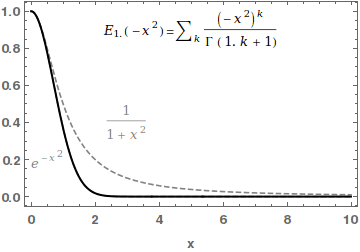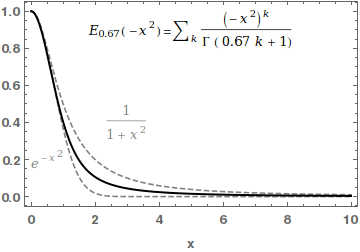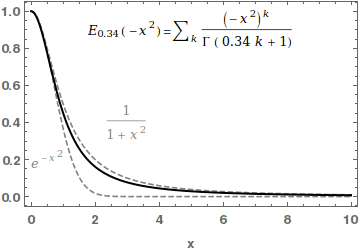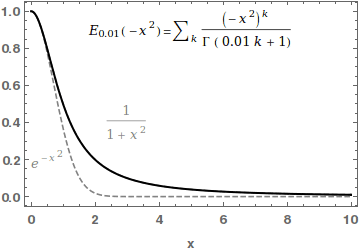
Mittag-Leffler Function
In mathematics, the Mittag-Leffler function E_ is a special function, a complex function which depends on two complex parameters \alpha and \beta. It may be defined by the following series when the real part of \alpha is strictly positive: :E_ (z) = \sum_^\infty \frac, where \Gamma(x) is the gamma function. When \beta=1, it is abbreviated as E_\alpha(z) = E_(z). For \alpha=0, the series above equals the Taylor expansion of the geometric series and consequently E_(z)=\frac\frac. In the case \alpha and \beta are real and positive, the series converges for all values of the argument z, so the Mittag-Leffler function is an entire function. This function is named after Gösta Mittag-Leffler. This class of functions are important in the theory of the fractional calculus. For \alpha >0 , the Mittag-Leffler function E_(z) is an entire function of order 1/\alpha, and is in some sense the simplest entire function of its order. The Mittag-Leffler function satisfies the recurrence pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History Of Calculus
Calculus, originally called infinitesimal calculus, is a mathematical discipline focused on limits, continuity, derivatives, integrals, and infinite series. Many elements of calculus appeared in ancient Greece, then in China and the Middle East, and still later again in medieval Europe and in India. Infinitesimal calculus was developed in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz independently of each other. An argument over priority led to the Leibniz–Newton calculus controversy which continued until the death of Leibniz in 1716. The development of calculus and its uses within the sciences have continued to the present day. Etymology In mathematics education, ''calculus'' denotes courses of elementary mathematical analysis, which are mainly devoted to the study of functions and limits. The word ''calculus'' is Latin for "small pebble" (the diminutive of '' calx,'' meaning "stone"), a meaning which still persists in medicine. Because such pebbles were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Institute Of Mathematics And Informatics
The Institute of Mathematics and Informatics was established in 1947 as Institute of Mathematics at the Bulgarian Academy of Sciences. Its name changed to Institute of Mathematics with Computing Centre in 1961, while from 1970 to 1988 the Institute together with the Faculty of Mathematics at Sofia University functioned in a unified structure, the Joint Centre of Mathematics and Mechanics. The present name was adopted in 1995. The Institute carries out scientific research in the fields of mathematics and informatics, as well as their applications to education, science, business and industry, government, etc. Members of the Institute hold teaching positions at a number of Bulgarian universities and colleges, providing also direction to Ph.D. and M.S. students. The Institute plays an important role in training gifted pupils, graduates, etc. for participating in major international competitions in mathematics and informatics. In particular, the Bulgarian team in mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bulgarian Academy Of Sciences
The Bulgarian Academy of Sciences (abbreviated BAS; bg, Българска академия на науките, ''Balgarska akademiya na naukite'', abbreviated ''БАН'') is the National Academy of Bulgaria, established in 1869. The Academy, with headquarters in Sofia, is autonomous and consists of a Society of Academicians, Correspondent Members and Foreign Members. It publishes and circulates different scientific works, encyclopaedias, dictionaries and journals, and runs its own publishing house. The activities are distributed in three main branches: ''Natural, mathematical and engineering sciences''; ''Biological, medical and agrarian sciences'' and ''Social sciences, humanities and art''. They are structured in 42 independent scientific institutes, and a dozen of laboratories and other sections. Julian Revalski has been the president of the BAS since 2016. As of 2021, its budget was 117,8 million leva (€60,2 million). History As Bulgaria was part of the Ottoman E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Mathematical Olympiad
The International Mathematical Olympiad (IMO) is a mathematical olympiad for pre-university students, and is the oldest of the International Science Olympiads. The first IMO was held in Romania in 1959. It has since been held annually, except in 1980. More than 100 countries, representing over 90% of the world's population, send teams of up to six students, plus one team leader, one deputy leader, and observers. The content ranges from extremely difficult algebra and pre-calculus problems to problems on branches of mathematics not conventionally covered in secondary or high school and often not at university level either, such as projective and complex geometry, functional equations, combinatorics, and well-grounded number theory, of which extensive knowledge of theorems is required. Calculus, though allowed in solutions, is never required, as there is a principle that anyone with a basic understanding of mathematics should understand the problems, even if the solutions req ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sofia University
Sofia University, "St. Kliment Ohridski" at the University of Sofia, ( bg, Софийски университет „Св. Климент Охридски“, ''Sofijski universitet „Sv. Kliment Ohridski“'') is the oldest higher education institution in Bulgaria. Founded on 1 October 1888, the edifice of the university was constructed between 1924 and 1934 with the financial support of the brothers Evlogi Georgiev and Hristo Georgiev (whose sculptures are now featured on its façade) and has an area of 18,624 m2 and a total of 324 premises. The university has 16 faculties and three departments, where over 21,000 students receive their education. The current rector is Anastas Gerdzhikov. It has been consistently ranked as the top university in Bulgaria according to national and international rankings, being constantly among the best four percent of world universities according to ''QS World University Rankings''. History The university was founded on 1 October 1888— ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Habilitation
Habilitation is the highest university degree, or the procedure by which it is achieved, in many European countries. The candidate fulfills a university's set criteria of excellence in research, teaching and further education, usually including a dissertation. The degree, abbreviated "Dr. habil." (Doctor habilitatus) or "PD" (for "Privatdozent"), is a qualification for professorship in those countries. The conferral is usually accompanied by a lecture to a colloquium as well as a public inaugural lecture. History and etymology The term ''habilitation'' is derived from the Medieval Latin , meaning "to make suitable, to fit", from Classical Latin "fit, proper, skillful". The degree developed in Germany in the seventeenth century (). Initially, habilitation was synonymous with "doctoral qualification". The term became synonymous with "post-doctoral qualification" in Germany in the 19th century "when holding a doctorate seemed no longer sufficient to guarantee a proficient transfe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus And Applied Analysis
''Fractional Calculus and Applied Analysis'' is a peer-reviewed mathematics journal published by Walter de Gruyter. It covers research on fractional calculus, special functions, integral transforms, and some closely related areas of applied analysis. The journal is abstracted and indexed in Science Citation Index Expanded, Scopus, Current Contents/Physical, Chemical and Earth Sciences, ''Zentralblatt MATH'', and ''Mathematical Reviews''. The journal's Founding Editors were Professors Eric Love, Ian Sneddon, Bogoljub Stanković, Rudolf Gorenflo, Danuta Przeworska-Rolewicz Danuta Przeworska-Rolewicz (25 May 1931 – 23 June 2012), was a Polish professor of mathematics and long-time employee of the Institute of Mathematics of the Polish Academy of Sciences. During World War II, as a child, she was a resistance fight ..., Gary Roach, Anatoly Kilbas, and Wen Chen. References External links * {{Official website, 1=https://www.degruyter.com/view/j/fca?lang=en Mathematics jour ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Year Of Birth Missing (living People)
A year or annus is the orbital period of a planetary body, for example, the Earth, moving in its orbit around the Sun. Due to the Earth's axial tilt, the course of a year sees the passing of the seasons, marked by change in weather, the hours of daylight, and, consequently, vegetation and soil fertility. In temperate and subpolar regions around the planet, four seasons are generally recognized: spring, summer, autumn and winter. In tropical and subtropical regions, several geographical sectors do not present defined seasons; but in the seasonal tropics, the annual wet and dry seasons are recognized and tracked. A calendar year is an approximation of the number of days of the Earth's orbital period, as counted in a given calendar. The Gregorian calendar, or modern calendar, presents its calendar year to be either a common year of 365 days or a leap year of 366 days, as do the Julian calendars. For the Gregorian calendar, the average length of the calendar yea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Living People
Related categories * :Year of birth missing (living people) / :Year of birth unknown * :Date of birth missing (living people) / :Date of birth unknown * :Place of birth missing (living people) / :Place of birth unknown * :Year of death missing / :Year of death unknown * :Date of death missing / :Date of death unknown * :Place of death missing / :Place of death unknown * :Missing middle or first names See also * :Dead people * :Template:L, which generates this category or death years, and birth year and sort keys. : {{DEFAULTSORT:Living people 21st-century people People by status ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |