|
Viewing Frustum
In 3D computer graphics, a viewing frustum or view frustum is the region of space in the modeled world that may appear on the screen; it is the field of view of a perspective virtual camera system. The view frustum is typically obtained by taking a geometrical frustum—that is a truncation with parallel planes—of the pyramid of vision, which is the adaptation of (idealized) '' cone of vision'' that a camera or eye would have to the rectangular viewports typically used in computer graphics. Some authors use ''pyramid of vision'' as a synonym for view frustum itself, i.e. consider it truncated. The exact shape of this region varies depending on what kind of camera lens is being simulated, but typically it is a frustum of a rectangular pyramid (hence the name). The planes that cut the frustum perpendicular to the viewing direction are called the ''near plane'' and the ''far plane''. Objects closer to the camera than the near plane or beyond the far plane are not drawn. Somet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hidden-surface Determination
In 3D computer graphics, hidden-surface determination (also known as shown-surface determination, hidden-surface removal (HSR), occlusion culling (OC) or visible-surface determination (VSD)) is the process of identifying what Computer representation of surfaces, surfaces and parts of surfaces can be seen from a particular viewing angle. A hidden-surface determination algorithm is a solution to the visibility problem, which was one of the first major problems in the field of 3D computer graphics. The process of hidden-surface determination is sometimes called hiding, and such an algorithm is sometimes called a hider. When referring to line rendering it is known as hidden-line removal. Hidden-surface determination is necessary to render a scene correctly, so that one may not view features hidden behind the model itself, allowing only the naturally viewable portion of the graphic to be visible. Background Hidden-surface determination is a process that identifies which surfaces are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transformation Matrix
In linear algebra, linear transformations can be represented by matrices. If T is a linear transformation mapping \mathbb^n to \mathbb^m and \mathbf x is a column vector with n entries, then there exists an m \times n matrix A, called the transformation matrix of T, such that: T( \mathbf x ) = A \mathbf x Note that A has m rows and n columns, whereas the transformation T is from \mathbb^n to \mathbb^m. There are alternative expressions of transformation matrices involving row vectors that are preferred by some authors. Uses Matrices allow arbitrary linear transformations to be displayed in a consistent format, suitable for computation. This also allows transformations to be composed easily (by multiplying their matrices). Linear transformations are not the only ones that can be represented by matrices. Some transformations that are non-linear on an n-dimensional Euclidean space R''n'' can be represented as linear transformations on the ''n''+1-dimensional space R''n''+1. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
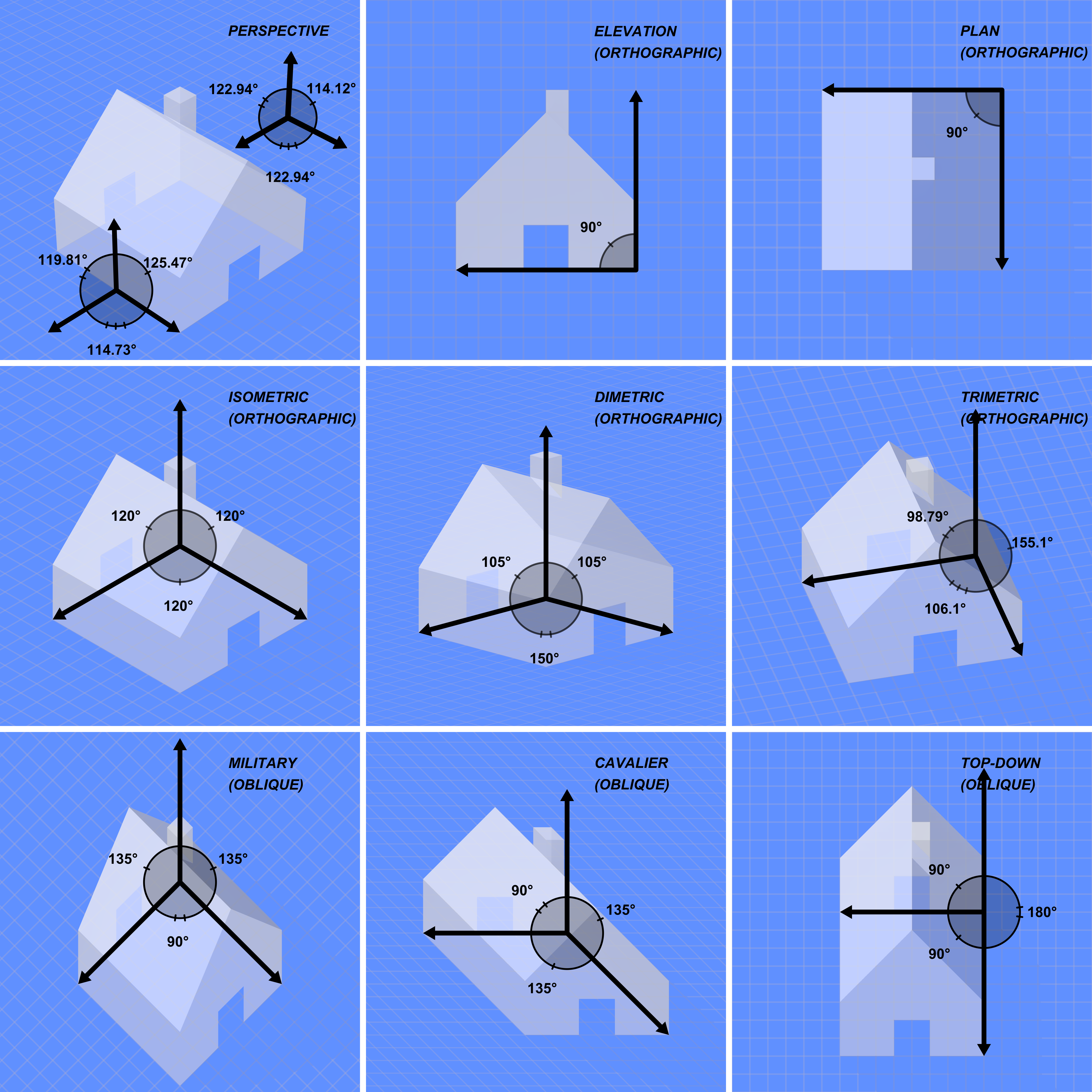
Projection Matrix (computer Graphics)
A 3D projection (or graphical projection) is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane. 3D projections use the primary qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element. The result is a graphic that contains conceptual properties to interpret the figure or image as not actually flat (2D), but rather, as a solid object (3D) being viewed on a 2D display. 3D objects are largely displayed on two-dimensional mediums (such as paper and computer monitors). As such, graphical projections are a commonly used design element; notably, in engineering drawing, drafting, and computer graphics. Projections can be calculated through employment of mathematical analysis and formulae, or by using various geometric and opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aspect Ratio (image)
The aspect ratio of an image is the ratio of its width to its height. It is expressed as two numbers separated by a colon, in the format width:height. Common aspect ratios are 1.85:1 and 2.39:1 in cinematography, 4:3 and 16:9 in television, and 3:2 in still photography and 1:1: Used for square images, often seen on social media platforms like Instagram, 21:9: An ultrawide aspect ratio popular for gaming and desktop monitors. Some common examples The common film aspect ratios used in cinemas are 1.85:1 and 2.39:1.The 2.39:1 ratio is commonly labeled 2.40:1, e.g., in the American Society of Cinematographers' ''American Cinematographer Manual'' (Many widescreen films before the 1970 Society of Motion Picture and Television Engineers, SMPTE revision used 2.35:1). Two common videography, videographic aspect ratios are 4:3 (1.:1), the universal video format of the 20th century, and 16:9 (1.:1), universal for high-definition television and European digital television. Other cinematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field Of View
The field of view (FOV) is the angle, angular extent of the observable world that is visual perception, seen at any given moment. In the case of optical instruments or sensors, it is a solid angle through which a detector is sensitive to electromagnetic radiation. It is further relevant in ''angle of view, photography''. Humans and animals In the context of human and primate vision, the term "field of view" is typically only used in the sense of a restriction to what is visible by external apparatus, like when wearing spectacles or virtual reality goggles. Note that eye movements are allowed in the definition but do not change the field of view when understood this way. If the analogy of the eye's retina working as a sensor is drawn upon, the corresponding concept in human (and much of animal vision) is the visual field. It is defined as "the number of degrees of visual angle during stable fixation of the eyes".Strasburger, Hans; Pöppel, Ernst (2002). Visual Field. In G. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Normal
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the curve at the point. A normal vector is a vector perpendicular to a given object at a particular point. A normal vector of length one is called a unit normal vector or normal direction. A curvature vector is a normal vector whose length is the curvature of the object. Multiplying a normal vector by results in the opposite vector, which may be used for indicating sides (e.g., interior or exterior). In three-dimensional space, a surface normal, or simply normal, to a surface at point is a vector perpendicular to the tangent plane of the surface at . The vector field of normal directions to a surface is known as '' Gauss map''. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounding Volume
In computer graphics and computational geometry, a bounding volume (or bounding region) for a set of objects is a closed region that completely contains the union of the objects in the set. Bounding volumes are used to improve the efficiency of geometrical operations, such as by using simple regions, having simpler ways to test for overlap. A bounding volume for a set of objects is also a bounding volume for the single object consisting of their union, and the other way around. Therefore, it is possible to confine the description to the case of a single object, which is assumed to be non-empty and bounded (finite). Uses Bounding volumes are most often used to accelerate certain kinds of tests. In ray tracing, bounding volumes are used in ray-intersection tests, and in many rendering algorithms, they are used for viewing frustum tests. If the ray or viewing frustum does not intersect the bounding volume, it cannot intersect the object contained within, allowing trivia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rendering (computer Graphics)
Rendering is the process of generating a physically-based rendering, photorealistic or Non-photorealistic rendering, non-photorealistic image from input data such as 3D models. The word "rendering" (in one of its senses) originally meant the task performed by an artist when depicting a real or imaginary thing (the finished artwork is also called a "architectural rendering, rendering"). Today, to "render" commonly means to generate an image or video from a precise description (often created by an artist) using a computer program. A application software, software application or component-based software engineering, component that performs rendering is called a rendering software engine, engine, render engine, : Rendering systems, rendering system, graphics engine, or simply a renderer. A distinction is made between Real-time computer graphics, real-time rendering, in which images are generated and displayed immediately (ideally fast enough to give the impression of motion or an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new Facet (geometry), facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids. Uniform truncation In general any polyhedron (or polytope) can also be truncated with a degree of freedom as to how deep the cut is, as shown in Conway polyhedron notation truncation operation. A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron (or regular polytope) which creates a resulting uniform polyhedron (uniform polytope) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra. In general all single ringed uniform polytopes have a uniform truncation. For example, the icosidodecahedron, represented as Schläfli symbols r or \begin 5 \\ 3 \end, and Coxeter-Dynkin diagram or has a uniform truncation, the truncate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid Of Vision
In 3D computer graphics, a viewing frustum or view frustum is the region of space in the modeled world that may appear on the screen; it is the field of view of a perspective virtual camera system. The view frustum is typically obtained by taking a geometrical frustum—that is a truncation with parallel planes—of the pyramid of vision, which is the adaptation of (idealized) '' cone of vision'' that a camera or eye would have to the rectangular viewports typically used in computer graphics. Some authors use ''pyramid of vision'' as a synonym for view frustum itself, i.e. consider it truncated. The exact shape of this region varies depending on what kind of camera lens is being simulated, but typically it is a frustum of a rectangular pyramid (hence the name). The planes that cut the frustum perpendicular to the viewing direction are called the ''near plane'' and the ''far plane''. Objects closer to the camera than the near plane or beyond the far plane are not drawn. Somet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viewport
A viewport is a polygon viewing region in computer graphics. In computer graphics theory, there are two region-like notions of relevance when rendering some objects to an image. In textbook terminology, the ''world coordinate window'' is the area of interest (meaning what the user wants to visualize) in some application-specific coordinates, e.g. miles, centimeters etc. The word ''window'' as used here should not be confused with the Window (computing), GUI window, i.e. the notion used in window managers. Rather it is an analogy with how a window limits what one can see outside a room. In contrast, the ''viewport'' is an area (typically rectangular) expressed in rendering-device-specific coordinates, e.g. pixels for screen coordinates, in which the objects of interest are going to be rendered. Clipping (computer graphics), Clipping to the world-coordinates window is usually applied to the objects before they are passed through the Coordinate system#Transformations , window-to-vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |