|
V. Balakrishnan (physicist)
V. Balakrishnan, (born 1943 as Venkataraman Balakrishnan) is an Indian theoretical physicist, who has worked in a number of fields and areas, including particle physics, many-body theory, the mechanical behavior of solids, dynamical systems, stochastic processes, and quantum dynamics. He is an accomplished researcher who has made important contributions to the theory of anelasticity, continuous-time random walks, and recurrences in dynamical systems. Education and career He received his undergraduate degree from St. Stephen’s College, Delhi and PhD from Brandeis University in 1970. After a decade at TIFR and IGCAR Kalpakkam, he joined IIT Madras as a Professor of Physics in 1980. He was elected a Fellow of the Indian Academy of Sciences in 1985. In addition to his research, Balakrishnan is a teacher of physics, known for his engaging teaching style. He has taught a wide range of courses over the past 30 years from introductory physics to quantum field theory to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
India
India, officially the Republic of India ( Hindi: ), is a country in South Asia. It is the seventh-largest country by area, the second-most populous country, and the most populous democracy in the world. Bounded by the Indian Ocean on the south, the Arabian Sea on the southwest, and the Bay of Bengal on the southeast, it shares land borders with Pakistan to the west; China, Nepal, and Bhutan to the north; and Bangladesh and Myanmar to the east. In the Indian Ocean, India is in the vicinity of Sri Lanka and the Maldives; its Andaman and Nicobar Islands share a maritime border with Thailand, Myanmar, and Indonesia. Modern humans arrived on the Indian subcontinent from Africa no later than 55,000 years ago., "Y-Chromosome and Mt-DNA data support the colonization of South Asia by modern humans originating in Africa. ... Coalescence dates for most non-European populations average to between 73–55 ka.", "Modern human beings—''Homo sapiens''—originated in Africa. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
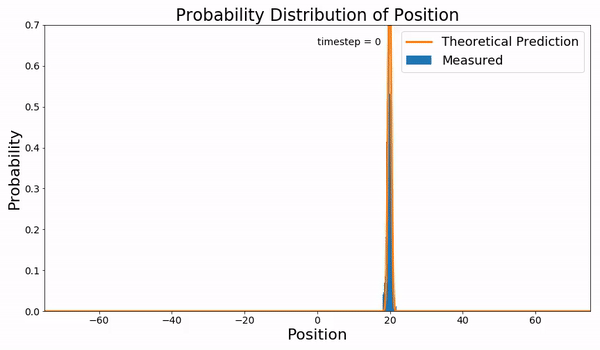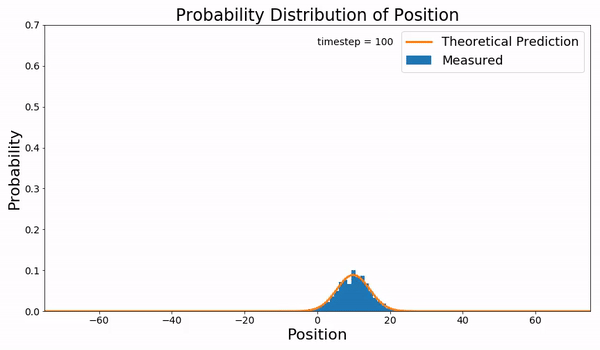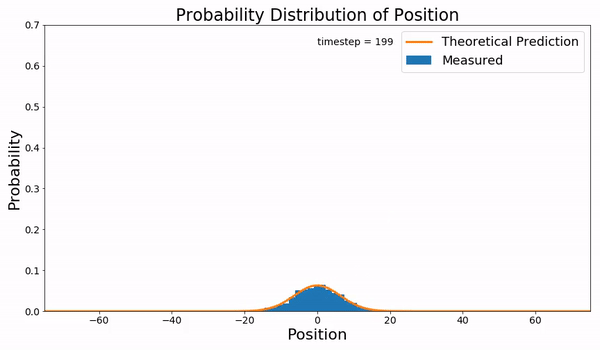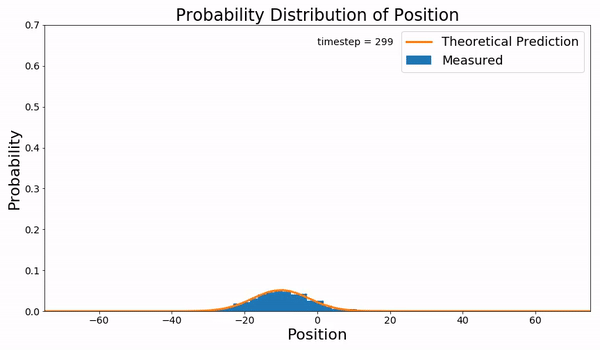
Continuous-time Random Walk
In mathematics, a continuous-time random walk (CTRW) is a generalization of a random walk where the wandering particle waits for a random time between jumps. It is a stochastic jump process with arbitrary distributions of jump lengths and waiting times. More generally it can be seen to be a special case of a Markov renewal process. Motivation CTRW was introduced by Montroll and Weiss as a generalization of physical diffusion process to effectively describe anomalous diffusion, i.e., the super- and sub-diffusive cases. An equivalent formulation of the CTRW is given by generalized master equations. A connection between CTRWs and diffusion equations with fractional time derivatives has been established. Similarly, time-space fractional diffusion equations can be considered as CTRWs with continuously distributed jumps or continuum approximations of CTRWs on lattices. Formulation A simple formulation of a CTRW is to consider the stochastic process X(t) defined by : X(t) = X_0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1943 Births
Events Below, the events of World War II have the "WWII" prefix. January * January 1 – WWII: The Soviet Union announces that 22 German divisions have been encircled at Stalingrad, with 175,000 killed and 137,650 captured. * January 4 – WWII: Greek-Polish athlete and saboteur Jerzy Iwanow-Szajnowicz is executed by the Germans at Kaisariani. * January 11 ** The United States and United Kingdom revise previously unequal treaty relationships with the Republic of China. ** Italian-American anarchist Carlo Tresca is assassinated in New York City. * January 13 – Anti-Nazi protests in Sofia result in 200 arrests and 36 executions. * January 14 – 24 – WWII: Casablanca Conference: Franklin D. Roosevelt, President of the United States; Winston Churchill, Prime Minister of the United Kingdom; and Generals Charles de Gaulle and Henri Giraud of the Free French forces meet secretly at the Anfa Hotel in Casablanca, Morocco, to plan the Allied European strategy for the next stage ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Living People
Related categories * :Year of birth missing (living people) / :Year of birth unknown * :Date of birth missing (living people) / :Date of birth unknown * :Place of birth missing (living people) / :Place of birth unknown * :Year of death missing / :Year of death unknown * :Date of death missing / :Date of death unknown * :Place of death missing / :Place of death unknown * :Missing middle or first names See also * :Dead people * :Template:L, which generates this category or death years, and birth year and sort keys. : {{DEFAULTSORT:Living people 21st-century people People by status ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brandeis University Alumni
Brandeis is a surname. People * Antonietta Brandeis (1848–1926), Czech-born Italian painter * Brandeis Marshall, American data scientist * Friedl Dicker-Brandeis, Austrian artist and Holocaust victim * Irma Brandeis, American Dante scholar *Louis Brandeis, U.S. Supreme Court Justice Named for Louis Brandeis ** Brandeis Brief, a 1908 document written by Brandeis as a litigator **Brandeis University, in Massachusetts, U.S. **Brandeis-Bardin Institute, now the Brandeis-Bardin Campus of American Jewish University, in California, U.S. ** Louis D. Brandeis School of Law, at the University of Louisville in Kentucky, U.S. ** Brandeis Medal, awarded by the University of Louisville's Louis D. Brandeis Society ** Brandeis Award (other), several different awards ** Kfar Brandeis (English: Brandeis village), a suburb of Hadera, Israel See also * Brandýs nad Labem-Stará Boleslav (german: Brandeis an der Elbe), a town in the Czech Republic * Brandýs nad Orlicí (german: Brandeis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Academic Staff Of IIT Madras
An academy (Attic Greek: Ἀκαδήμεια; Koine Greek Ἀκαδημία) is an institution of secondary or tertiary higher learning (and generally also research or honorary membership). The name traces back to Plato's school of philosophy, founded approximately 385 BC at Akademia, a sanctuary of Athena, the goddess of wisdom and skill, north of Athens, Greece. Etymology The word comes from the ''Academy'' in ancient Greece, which derives from the Athenian hero, ''Akademos''. Outside the city walls of Athens, the gymnasium was made famous by Plato as a center of learning. The sacred space, dedicated to the goddess of wisdom, Athena, had formerly been an olive grove, hence the expression "the groves of Academe". In these gardens, the philosopher Plato conversed with followers. Plato developed his sessions into a method of teaching philosophy and in 387 BC, established what is known today as the Old Academy. By extension, ''academia'' has come to mean the accumulation, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fellows Of The Indian Academy Of Sciences
Fellows may refer to Fellow, in plural form. Fellows or Fellowes may also refer to: Places *Fellows, California, USA *Fellows, Wisconsin, ghost town, USA Other uses *Fellows Auctioneers, established in 1876. * Fellowes, Inc., manufacturer of workspace products *Fellows, a partner in the firm of English canal carriers, Fellows Morton & Clayton *Fellows (surname) See also *North Fellows Historic District The North Fellows Historic District is a historic district located in Ottumwa, Iowa, United States. The city experienced a housing boom after World War II. This north side neighborhood of single-family brick homes built between 1945 and 1959 ..., listed on the National Register of Historic Places in Wapello County, Iowa * Justice Fellows (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamsa Balakrishnan
The ''hamsa'' ( ar, خمسة, khamsa) is a palm-shaped amulet popular throughout North Africa and in the Middle East and commonly used in jewellery and wall hangings.Bernasek et al., 2008p. 12Sonbol, 2005pp. 355–359 Depicting the open right hand, an image recognized and used as a sign of protection in many times throughout history, the ''hamsa'' has been traditionally believed to provide defense against the evil eye. ''Khamsah'' is an Arabic word that means "five", but also refers to images of "the five fingers of the hand".Zenner, 1988p. 284World Institute for Advanced Phenomenological Research and Learning (Belmont, Estados Unidos), 1991p. 219Drazin, 2009p. 268 In Jewish culture, the ''hamsa'' is associated with the number five because of the five fingers depicted on the hand, and because the word ''khamsa'' is cognate to the Hebrew ''ḥamishah'' (חֲמִישָׁה), which also means "five." The ''Hamsa'' has also been known as the Hand of Fatima after the daughter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solitons
In mathematics and physics, a soliton or solitary wave is a self-reinforcing wave packet that maintains its shape while it propagates at a constant velocity. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium. (Dispersive effects are a property of certain systems where the speed of a wave depends on its frequency.) Solitons are the solutions of a widespread class of weakly nonlinear dispersive partial differential equations describing physical systems. The soliton phenomenon was first described in 1834 by John Scott Russell (1808–1882) who observed a solitary wave in the Union Canal in Scotland. He reproduced the phenomenon in a wave tank and named it the " Wave of Translation". Definition A single, consensus definition of a soliton is difficult to find. ascribe three properties to solitons: # They are of permanent form; # They are localized within a region; # They can interact with other solitons, and emerge from the collision unchange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langevin Equation
In physics, a Langevin equation (named after Paul Langevin) is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid. Brownian motion as a prototype The original Langevin equation describes Brownian motion, the apparently random movement of a particle in a fluid due to collisions with the molecules of the fluid, m\frac=-\lambda \mathbf+\boldsymbol\left( t\right). Here, \mathbf is the velocity of the particle, and m is its mass. The force acting on the particle is written as a sum of a viscous force ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |