|
Ushiki's Theorem
In mathematics, particularly in the study of functions of several complex variables, Ushiki's theorem, named after S. Ushiki, states that certain well-behaved functions cannot have certain kinds of well-behaved invariant manifolds. The theorem A biholomorphic mapping F:\mathbb^n\to\mathbb^n cannot have a 1-dimensional compact smooth invariant manifold. In particular, such a map cannot have a homoclinic connection or heteroclinic connection. Commentary Invariant manifolds typically appear as solutions of certain asymptotic problems in dynamical systems. The most common is the stable manifold or its kin, the unstable manifold. The publication Ushiki's theorem was published in 1980.S. Ushiki. Sur les liaisons-cols des systèmes dynamiques analytiques. C. R. Acad. Sci. Paris, 291(7):447–449, 1980 The theorem appeared in print again several years later, in a certain Russian journal, by an author apparently unaware of Ushiki's work. An application The standard map ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Several Complex Variable
The theory of functions of several complex variables is the branch of mathematics dealing with complex number, complex-valued functions. The name of the field dealing with the properties of function of several complex variables is called several complex variables (and analytic space), that has become a common name for that whole field of study and Mathematics Subject Classification has, as a top-level heading. A function (mathematics), function f:(z_1,z_2, \ldots, z_n) \rightarrow f(z_1,z_2, \ldots, z_n) is -tuples of complex numbers, classically studied on #The complex coordinate space, the complex coordinate space \Complex^n. As in complex analysis, complex analysis of functions of one variable, which is the case , the functions studied are ''holomorphic function, holomorphic'' or ''complex analytic'' so that, locally, they are power series in the variables . Equivalently, they are locally uniform convergence, uniform limits of polynomials; or locally Lp space, square-integrable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
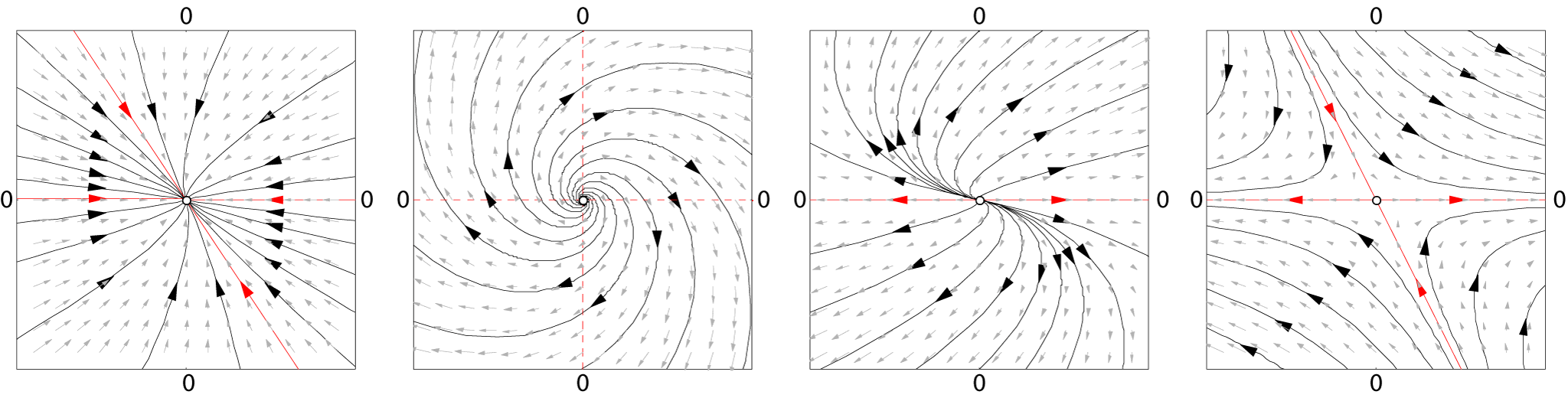
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equichordal Point Problem
In Euclidean plane geometry, the equichordal point problem is the question whether a closed planar convex body can have two equichordal points. The problem was originally posed in 1916 by Fujiwara and in 1917 by Wilhelm Blaschke, Hermann Rothe, and Roland Weitzenböck. W. Blaschke, H. Rothe, and R. Weitzenböck. Aufgabe 552. Arch. Math. Phys., 27:82, 1917 A generalization of this problem statement was answered in the negative in 1997 by Marek R. Rychlik. Problem statement An equichordal curve is a closed planar curve for which a point in the plane exists such that all chords passing through this point are equal in length. Such a point is called an equichordal point. It is easy to construct equichordal curves with a single equichordal point, particularly when the curves are symmetric; the simplest construction is a circle. It has long only been conjectured that no convex equichordal curve with two equichordal points can exist. More generally, it was asked whether there exists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Melnikov Distance
In mathematics, the Melnikov method is a tool to identify the existence of chaos in a class of dynamical systems under periodic perturbation. Introduction The Melnikov method is used in many cases to predict the occurrence of chaotic orbits in non-autonomous smooth nonlinear systems under periodic perturbation. According to the method, it is possible to construct a function called the "Melnikov function" which can be used to predict either regular or chaotic behavior of a dynamical system. Thus, the Melnikov function will be used to determine a measure of distance between stable and unstable manifolds in the Poincaré map. Moreover, when this measure is equal to zero, by the method, those manifolds crossed each other transversally and from that crossing the system will become chaotic. This method appeared in 1890 by H. Poincaré and by V. Melnikov in 1963 and could be called the "Poincaré-Melnikov Method". Moreover, it was described by several textbooks as Guckenheimer & Holme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Map
The standard map (also known as the Chirikov–Taylor map or as the Chirikov standard map) is an area-preserving chaotic map from a square with side 2\pi onto itself. It is constructed by a Poincaré's surface of section of the kicked rotator, and is defined by: :p_ = p_n + K \sin(\theta_n) :\theta_ = \theta_n + p_ where p_n and \theta_n are taken modulo 2\pi. The properties of chaos of the standard map were established by Boris Chirikov in 1969. Physical model This map describes the Poincaré's surface of section of the motion of a simple mechanical system known as the kicked rotator. The kicked rotator consists of a stick that is free of the gravitational force, which can rotate frictionlessly in a plane around an axis located in one of its tips, and which is periodically kicked on the other tip. The standard map is a surface of section applied by a stroboscopic projection on the variables of the kicked rotator. The variables \theta_n and p_n respectively determine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stable Manifold
In mathematics, and in particular the study of dynamical systems, the idea of ''stable and unstable sets'' or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor. In the case of hyperbolic dynamics, the corresponding notion is that of the hyperbolic set. Physical example The gravitational tidal forces acting on the rings of Saturn provide an easy-to-visualize physical example. The tidal forces flatten the ring into the equatorial plane, even as they stretch it out in the radial direction. Imagining the rings to be sand or gravel particles ("dust") in orbit around Saturn, the tidal forces are such that any perturbations that push particles above or below the equatorial plane results in that particle feeling a restoring force, pushing it back into the plane. Particles effectively oscillate in a harmonic well, damped by collisions. The stable direction is perpendicular to the ring. The unstable di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heteroclinic Connection
{{unreferenced, date=December 2010 In dynamical systems, a branch of mathematics, a structure formed from the stable manifold and unstable manifold of a fixed point. Definition for maps Let f:M\to M be a map defined on a manifold M, with a fixed point p. Let W^s(f,p) and W^u(f,p) be the stable manifold and the unstable manifold of the fixed point p, respectively. Let V be a connected invariant manifold such that : V\subseteq W^s(f,p)\cap W^u(f,p) Then V is called a homoclinic connection. Heteroclinic connection It is a similar notion, but it refers to two fixed points, p and q. The condition satisfied by V is replaced with: :V\subseteq W^s(f,p)\cap W^u(f,q) This notion is not symmetric with respect to p and q. Homoclinic and heteroclinic intersections When the invariant manifolds W^s(f,p) and W^u(f,q), possibly with p=q, intersect but there is no homoclinic/heteroclinic connection, a different structure is formed by the two manifolds, sometimes referred to as the homoclini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-behaved
In mathematics, when a mathematical phenomenon runs counter to some intuition, then the phenomenon is sometimes called pathological. On the other hand, if a phenomenon does not run counter to intuition, it is sometimes called well-behaved. These terms are sometimes useful in mathematical research and teaching, but there is no strict mathematical definition of pathological or well-behaved. In analysis A classic example of a pathology is the Weierstrass function, a function that is continuous everywhere but differentiable nowhere. The sum of a differentiable function and the Weierstrass function is again continuous but nowhere differentiable; so there are at least as many such functions as differentiable functions. In fact, using the Baire category theorem, one can show that continuous functions are generically nowhere differentiable. Such examples were deemed pathological when they were first discovered: To quote Henri Poincaré: Since Poincaré, nowhere differentiable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homoclinic Connection
{{unreferenced, date=December 2010 In dynamical systems, a branch of mathematics, a structure formed from the stable manifold and unstable manifold of a fixed point. Definition for maps Let f:M\to M be a map defined on a manifold M, with a fixed point p. Let W^s(f,p) and W^u(f,p) be the stable manifold and the unstable manifold of the fixed point p, respectively. Let V be a connected invariant manifold such that : V\subseteq W^s(f,p)\cap W^u(f,p) Then V is called a homoclinic connection. Heteroclinic connection It is a similar notion, but it refers to two fixed points, p and q. The condition satisfied by V is replaced with: :V\subseteq W^s(f,p)\cap W^u(f,q) This notion is not symmetric with respect to p and q. Homoclinic and heteroclinic intersections When the invariant manifolds W^s(f,p) and W^u(f,q), possibly with p=q, intersect but there is no homoclinic/heteroclinic connection, a different structure is formed by the two manifolds, sometimes referred to as the homoclini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Manifold
In dynamical systems, a branch of mathematics, an invariant manifold is a topological manifold that is invariant under the action of the dynamical system. Examples include the slow manifold, center manifold, stable manifold, stable manifold, unstable manifold, subcenter manifold and inertial manifold. Typically, although by no means always, invariant manifolds are constructed as a 'perturbation' of an invariant subspace about an equilibrium. In dissipative systems, an invariant manifold based upon the gravest, longest lasting modes forms an effective low-dimensional, reduced, model of the dynamics. Definition Consider the differential equation dx/dt = f(x),\ x \in \mathbb R^n, with flow x(t)=\phi_t(x_0) being the solution of the differential equation with x(0)=x_0. A set S \subset \mathbb R^n is called an ''invariant set'' for the differential equation if, for each x_0 \in S, the solution t \mapsto \phi_t(x_0), defined on its maximal interval of existence, has its image in S. Alt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |