|
Upthrust
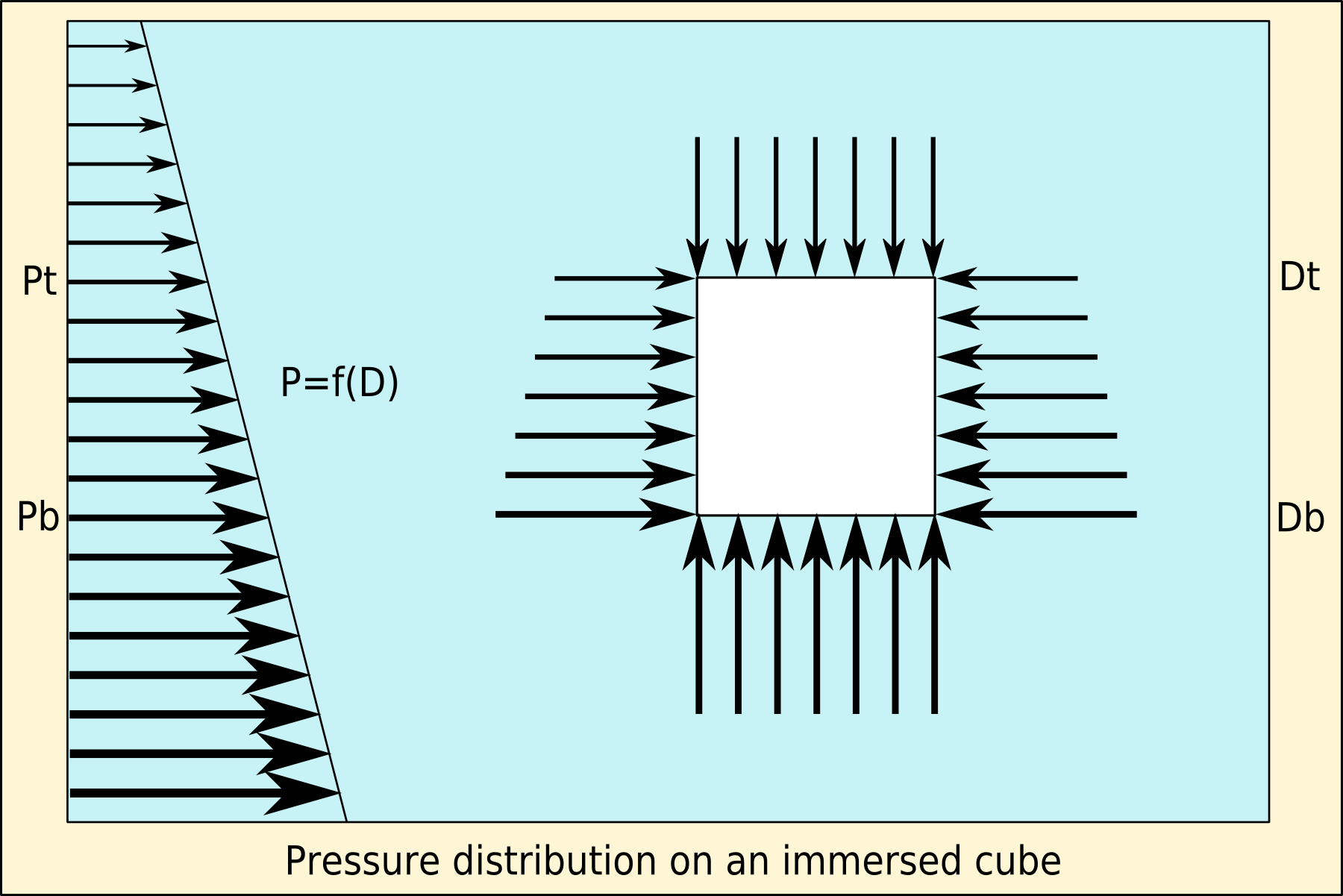
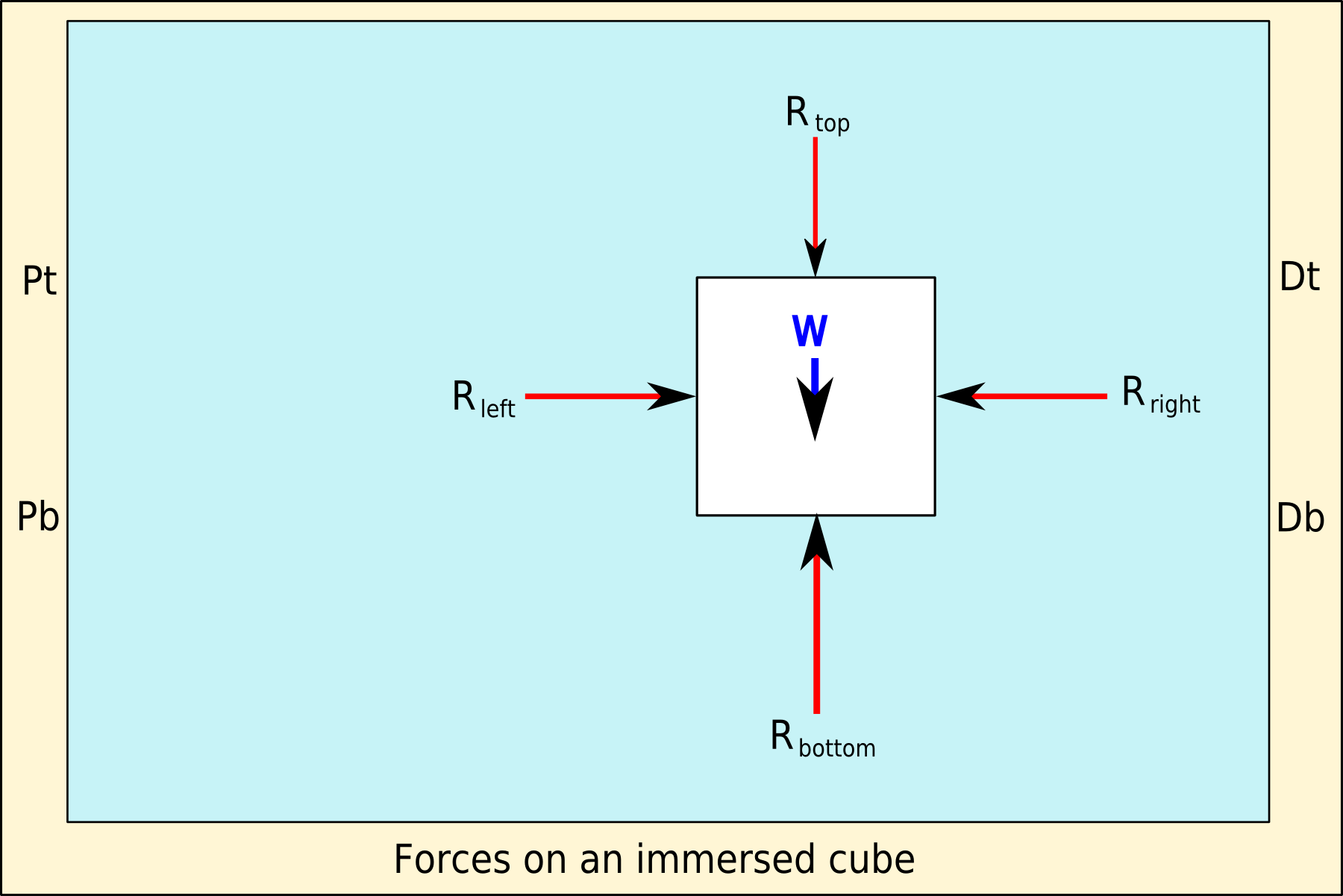
Buoyancy (), or upthrust, is an upward force exerted by a fluid that opposes the weight of a partially or fully immersed object. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the displaced fluid. For this reason, an object whose average density is greater than that of the fluid in which it is submerged tends to sink. If the object is less dense than the liquid, the force can keep the object afloat. This can occur only in a non- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buoyancy
Buoyancy (), or upthrust, is an upward force exerted by a fluid that opposes the weight of a partially or fully immersed object. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the displaced fluid. For this reason, an object whose average density is greater than that of the fluid in which it is submerged tends to sink. If the object is less dense than the liquid, the force can keep the object afloat. This can occur only in a no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) to float on a water surface without becoming even partly submerged. At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion). There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract. Second is a tangential force parallel to the surface of the liquid. This ''tangential'' force is generally referred to as the surface tension. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane. But this analogy must not be taken too far as the tension in an elastic membrane is dependent on the amount of deformation of the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seawater
Seawater, or salt water, is water from a sea or ocean. On average, seawater in the world's oceans has a salinity of about 3.5% (35 g/L, 35 ppt, 600 mM). This means that every kilogram (roughly one liter by volume) of seawater has approximately of dissolved salts (predominantly sodium () and chloride () ions). The average density at the surface is 1.025 kg/L. Seawater is denser than both fresh water and pure water (density 1.0 kg/L at ) because the dissolved salts increase the mass by a larger proportion than the volume. The freezing point of seawater decreases as salt concentration increases. At typical salinity, it freezes at about . The coldest seawater still in the liquid state ever recorded was found in 2010, in a stream under an Antarctic glacier: the measured temperature was . Seawater pH is typically limited to a range between 7.5 and 8.4. However, there is no universally accepted reference pH-scale for seawater and the difference between measurement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Net Force , a young adult novel series
{{disambiguation ...
Net Force may refer to: * Net force, the overall force acting on an object * ''NetForce'' (film), a 1999 American television film * Tom Clancy's Net Force, a novel series * Tom Clancy's Net Force Explorers Tom Clancy's Net Force Explorers or Net Force Explorers is a series of young adult fiction, young adult novels created by Tom Clancy and Steve Pieczenik as a spin-off of the military fiction series Tom Clancy's Net Force. The first novel was pub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag). This is the steady gain in speed caused exclusively by the force of gravitational attraction. All bodies accelerate in vacuum at the same rate, regardless of the masses or compositions of the bodies; the measurement and analysis of these rates is known as gravimetry. At a fixed point on the surface, the magnitude of Earth's gravity results from combined effect of gravitation and the centrifugal force from Earth's rotation. At different points on Earth's surface, the free fall acceleration ranges from , depending on altitude, latitude, and longitude. A conventional standard value is defined exactly as . Locations of significant variation from this value are known as gravity anomalies. This does not take into account other effects, such as buoyancy or drag. Relation to the Universal Law Newton's law of universal gravitation states that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss Theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem which relates the '' flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume enclosed. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called the "flux" through the surface, is equal to the volume integral of the divergence over the region inside the surface. Intuitively, it states that "the sum of all sources of the field in a region (with sinks regarded as negative sources) gives the net flux out of the region". The divergence theorem is an important result for the mathematics of physics and engineering, particularly in electrostatics and fluid dynamics. In these fields, it is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to integration by parts. In two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume Integral
In mathematics (particularly multivariable calculus), a volume integral (∭) refers to an integral over a 3-dimensional domain; that is, it is a special case of multiple integrals. Volume integrals are especially important in physics for many applications, for example, to calculate flux densities. In coordinates It can also mean a triple integral within a region D \subset \R^3 of a function f(x,y,z), and is usually written as: \iiint_D f(x,y,z)\,dx\,dy\,dz. A volume integral in cylindrical coordinates is \iiint_D f(\rho,\varphi,z) \rho \,d\rho \,d\varphi \,dz, and a volume integral in spherical coordinates (using the ISO convention for angles with \varphi as the azimuth and \theta measured from the polar axis (see more on conventions)) has the form \iiint_D f(r,\theta,\varphi) r^2 \sin\theta \,dr \,d\theta\, d\varphi . Example Integrating the equation f(x,y,z) = 1 over a unit cube yields the following result: \int_0^1 \int_0^1 \int_0^1 1 \,dx \,dy \,dz = \int_0^1 \int_0^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one may integrate a scalar field (that is, a function of position which returns a scalar as a value) over the surface, or a vector field (that is, a function which returns a vector as value). If a region R is not flat, then it is called a ''surface'' as shown in the illustration. Surface integrals have applications in physics, particularly with the theories of classical electromagnetism. Surface integrals of scalar fields Assume that ''f'' is a scalar, vector, or tensor field defined on a surface ''S''. To find an explicit formula for the surface integral of ''f'' over ''S'', we need to parameterize ''S'' by defining a system of curvilinear coordinates on ''S'', like the latitude and longitude on a sphere. Let such a parameterization be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kronecker Delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise: \delta_ = \begin 0 &\text i \neq j, \\ 1 &\text i=j. \end or with use of Iverson brackets: \delta_ = =j, where the Kronecker delta is a piecewise function of variables and . For example, , whereas . The Kronecker delta appears naturally in many areas of mathematics, physics and engineering, as a means of compactly expressing its definition above. In linear algebra, the identity matrix has entries equal to the Kronecker delta: I_ = \delta_ where and take the values , and the inner product of vectors can be written as \mathbf\cdot\mathbf = \sum_^n a_\delta_b_ = \sum_^n a_ b_. Here the Euclidean vectors are defined as -tuples: \mathbf = (a_1, a_2, \dots, a_n) and \mathbf= (b_1, b_2, ..., b_n) and the last step is obtained by using the values of the Kronecker delta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Stress Tensor
In continuum mechanics, the Cauchy stress tensor \boldsymbol\sigma, true stress tensor, or simply called the stress tensor is a second order tensor named after Augustin-Louis Cauchy. The tensor consists of nine components \sigma_ that completely define the state of stress at a point inside a material in the deformed state, placement, or configuration. The tensor relates a unit-length direction vector e to the traction vector T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sigma_e_i, or, :\leftright\leftrightcdot \leftright The SI units of both stress tensor and traction vector are N/m2, corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of materi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrostatic Weighing
Hydrostatic weighing, also referred to as underwater weighing, hydrostatic body composition analysis and hydrodensitometry, is a technique for measuring the density of a living person's body. It is a direct application of Archimedes' principle, that an object displaces its own volume of water. Method The procedure is based on Archimedes' principle, which states that: ''The buoyant force which water exerts on an immersed object is equal to the weight of water that the object displaces.'' Example 1: If a block of solid stone weighs 3 kilograms on dry land and 2 kilogram when immersed in a tub of water, then it has displaced 1 kilogram of water. Since 1 liter of water weighs 1 kilogram (at 4 °C), it follows that the volume of the block is 1 liter and the density (mass/volume) of the stone is 3 kilograms/liter. Example 2: Consider a larger block of the same stone material as in Example 1 but with a 1-liter cavity inside of the same amount of stone. The block would still wei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
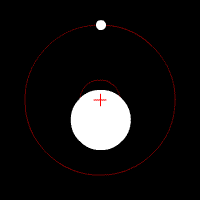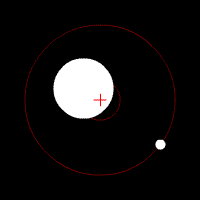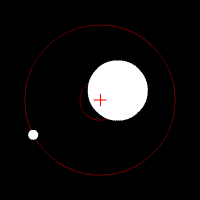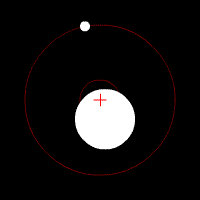
Dasymeter
A dasymeter was meant initially as a device to demonstrate the buoyant effect of gases like air (as shown in the adjacent pictures). A dasymeter which allows weighing acts as a densimeter used to measure the density of gases. Principle The Principle of Archimedes permits to derive a formula which does not rely on any information of volume: a sample, the big sphere in the adjacent images, of known mass-density is weighed in vacuum and then immersed into the gas and weighed again. : \frac = \frac \, :(The above formula was taken from the article buoyancy and still has to be solved for the density of the gas.) :From the known mass density of the sample (sphere) and its two weight-values, the mass-density of the gas can be calculated as: : = \frac \times Construction and use It consists of a thin sphere made of glass, ideally with an average density close to that of the gas to be investigated. This sphere is immersed in the gas and weighed. History of the dasymeter T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Seawater")
