|
Universal Instantiation
In predicate logic, universal instantiation (UI; also called universal specification or universal elimination, and sometimes confused with '' dictum de omni'') is a valid rule of inference from a truth about each member of a class of individuals to the truth about a particular individual of that class. It is generally given as a quantification rule for the universal quantifier but it can also be encoded in an axiom schema. It is one of the basic principles used in quantification theory. Example: "All dogs are mammals. Fido is a dog. Therefore Fido is a mammal." Formally, the rule as an axiom schema is given as : \forall x \, A \Rightarrow A\, for every formula ''A'' and every term ''t'', where A\ is the result of substituting ''t'' for each ''free'' occurrence of ''x'' in ''A''. \, A\ is an instance of \forall x \, A. And as a rule of inference it is :from \vdash \forall x A infer \vdash A \ . Irving Copi noted that universal instantiation "... follows from variants of ru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rule Of Inference
Rules of inference are ways of deriving conclusions from premises. They are integral parts of formal logic, serving as norms of the Logical form, logical structure of Validity (logic), valid arguments. If an argument with true premises follows a rule of inference then the conclusion cannot be false. ''Modus ponens'', an influential rule of inference, connects two premises of the form "if P then Q" and "P" to the conclusion "Q", as in the argument "If it rains, then the ground is wet. It rains. Therefore, the ground is wet." There are many other rules of inference for different patterns of valid arguments, such as ''modus tollens'', disjunctive syllogism, constructive dilemma, and existential generalization. Rules of inference include rules of implication, which operate only in one direction from premises to conclusions, and rules of replacement, which state that two expressions are equivalent and can be freely swapped. Rules of inference contrast with formal fallaciesinvalid argu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Consequence
Logical consequence (also entailment or logical implication) is a fundamental concept in logic which describes the relationship between statement (logic), statements that hold true when one statement logically ''follows from'' one or more statements. A Validity (logic), valid logical argument is one in which the Consequent, conclusion is entailed by the premises, because the conclusion is the consequence of the premises. The philosophical analysis of logical consequence involves the questions: In what sense does a conclusion follow from its premises? and What does it mean for a conclusion to be a consequence of premises?Beall, JC and Restall, Greg, Logical Consequence' The Stanford Encyclopedia of Philosophy (Fall 2009 Edition), Edward N. Zalta (ed.). All of philosophical logic is meant to provide accounts of the nature of logical consequence and the nature of logical truth. Logical consequence is logical truth, necessary and Formalism (philosophy of mathematics), formal, by wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Existential Quantification
Existentialism is a family of philosophy, philosophical views and inquiry that explore the human individual's struggle to lead an Authenticity (philosophy), authentic life despite the apparent Absurdity#The Absurd, absurdity or incomprehensibility of existence. In examining meaning of life, meaning, purpose, and value (ethics), value, existentialist thought often includes concepts such as existential crisis, existential crises, Angst#Existentialist angst, angst, courage, and freedom. Existentialism is associated with several 19th- and 20th-century European philosophers who shared an emphasis on the human subject, despite often profound differences in thought. Among the 19th-century figures now associated with existentialism are philosophers Søren Kierkegaard and Friedrich Nietzsche, as well as novelist Fyodor Dostoevsky, all of whom critiqued rationalism and concerned themselves with the problem of meaning (philosophy), meaning. The word ''existentialism'', however, was not coin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Existential Instantiation
In predicate logic, existential instantiation (also called existential elimination) is a rule of inference which says that, given a formula of the form (\exists x) \phi(x), one may infer \phi(c) for a new constant symbol ''c''. The rule has the restrictions that the constant ''c'' introduced by the rule must be a new term that has not occurred earlier in the proof, and it also must not occur in the conclusion of the proof. It is also necessary that every instance of x which is bound to \exists x must be uniformly replaced by ''c''. This is implied by the notation P\left(\right), but its explicit statement is often left out of explanations. In one formal notation, the rule may be denoted by :\exists x P \left(\right) \implies P \left(\right) where ''a'' is a new constant symbol that has not appeared in the proof. See also * Existential fallacy * Universal instantiation In predicate logic, universal instantiation (UI; also called universal specification or universal eliminat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
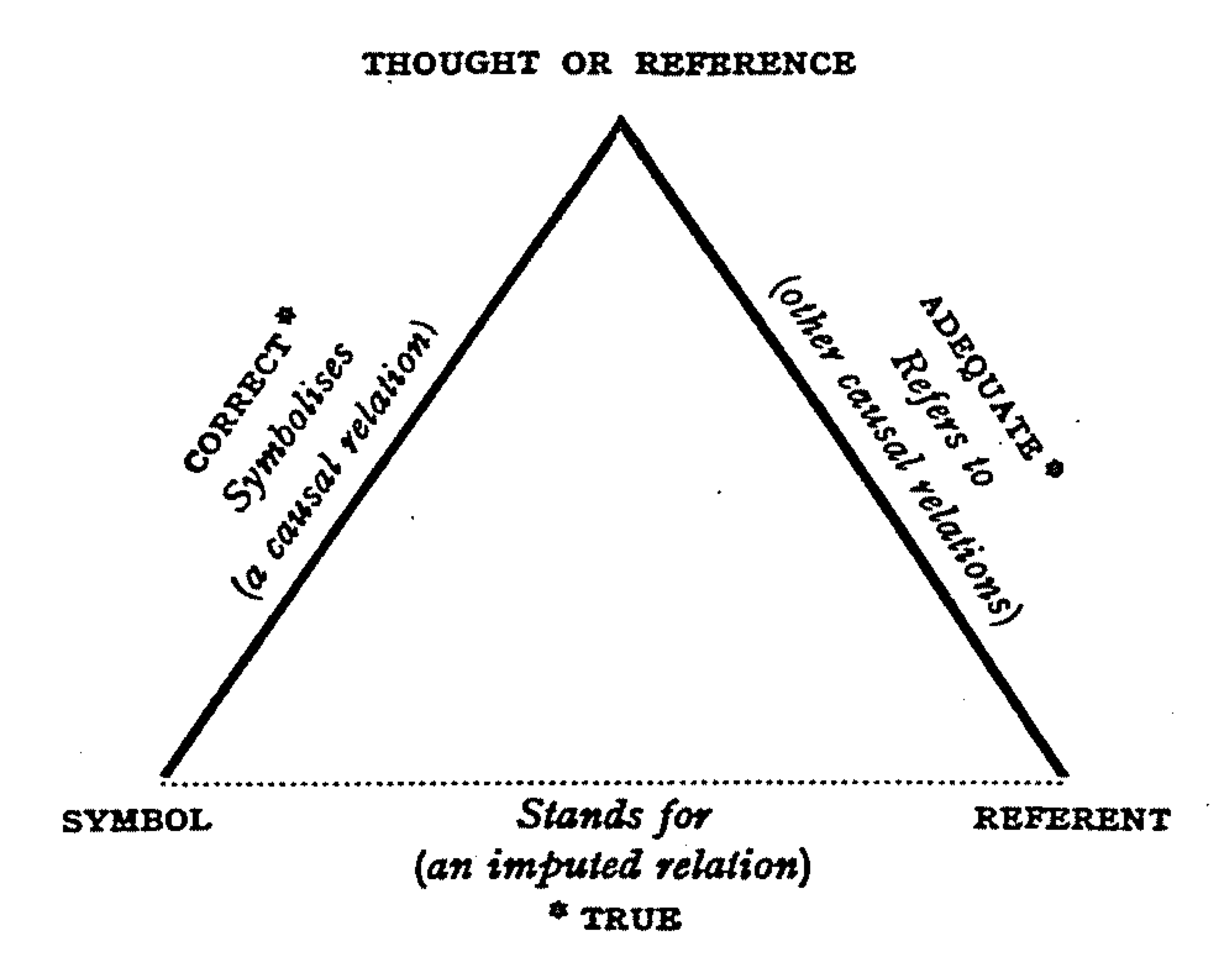
Reference
A reference is a relationship between objects in which one object designates, or acts as a means by which to connect to or link to, another object. The first object in this relation is said to ''refer to'' the second object. It is called a ''name'' for the second object. The next object, the one to which the first object refers, is called the '' referent'' of the first object. A name is usually a phrase or expression, or some other symbolic representation. Its referent may be anything – a material object, a person, an event, an activity, or an abstract concept. References can take on many forms, including: a thought, a sensory perception that is audible ( onomatopoeia), visual (text), olfactory, or tactile, emotional state, relationship with other, spacetime coordinates, symbolic or alpha-numeric, a physical object, or an energy projection. In some cases, methods are used that intentionally hide the reference from some observers, as in cryptography. References feature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantification (logic)
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier \forall in the first-order formula \forall x P(x) expresses that everything in the domain satisfies the property denoted by P. On the other hand, the existential quantifier \exists in the formula \exists x P(x) expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable. The most commonly used quantifiers are \forall and \exists. These quantifiers are standardly defined as duals; in classical logic: each can be defined in terms of the other using negation. They can also be used to define more complex quantifiers, as in the formula \neg \exists x P(x) which expresses that nothing ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Existential Generalization
In predicate logic, existential generalization (also known as existential introduction, ∃I) is a valid rule of inference that allows one to move from a specific statement, or one instance, to a quantified generalized statement, or existential proposition. In first-order logic, it is often used as a rule for the existential quantifier (\exists) in formal proofs. Example: "Rover loves to wag his tail. Therefore, something loves to wag its tail." Example: "Alice made herself a cup of tea. Therefore, Alice made someone a cup of tea." Example: "Alice made herself a cup of tea. Therefore, someone made someone a cup of tea." In the Fitch-style calculus: : Q(a) \to\ \exists\, Q(x) , where Q(a) is obtained from Q(x) by replacing all its free occurrences of x (or some of them) by a. Quine According to Willard Van Orman Quine, universal instantiation In predicate logic, universal instantiation (UI; also called universal specification or universal elimination, and sometimes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Willard Van Orman Quine
Willard Van Orman Quine ( ; known to his friends as "Van"; June 25, 1908 – December 25, 2000) was an American philosopher and logician in the analytic tradition, recognized as "one of the most influential philosophers of the twentieth century". He was the Edgar Pierce Chair of Philosophy at Harvard University from 1956 to 1978. Quine was a teacher of logic and set theory. He was famous for his position that first-order logic is the only kind worthy of the name, and developed his own system of mathematics and set theory, known as New Foundations. In the philosophy of mathematics, he and his Harvard colleague Hilary Putnam developed the Quine–Putnam indispensability argument, an argument for the Philosophy of mathematics#Empiricism, reality of mathematical entities.Colyvan, Mark"Indispensability Arguments in the Philosophy of Mathematics" The Stanford Encyclopedia of Philosophy (Fall 2004 Edition), Edward N. Zalta (ed.). He was the main proponent of the view that philosophy is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stanisław Jaśkowski
Stanisław Jaśkowski (Polish pronunciation: ; 22 April 1906, in Warsaw – 16 November 1965, in Warsaw) was a Polish logician who made important contributions to proof theory and formal semantics. He was a student of Jan Łukasiewicz and a member of the Lwów–Warsaw School of Logic. He is regarded as one of the founders of natural deduction, which he discovered independently of Gerhard Gentzen in the 1930s. He is also known for his research into paraconsistent logic. Upon his death, his name was added to the Genius Wall of Fame. He was the President (rector) of the Nicolaus Copernicus University in Toruń. Life and career He was born in 1906 in Warsaw to father Feliks Jaśkowski and mother Kazimiera (nee Dzierzbicka). In 1924, he graduated from high school in Zakopane and enrolled at the University of Warsaw to study mathematics. He was taught mathematical logic under Jan Łukasiewicz and participated in the Polish Mathematicians' Congresses in Lviv (1927) and Vilnius (1931) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gerhard Gentzen
Gerhard Karl Erich Gentzen (24 November 1909 – 4 August 1945) was a German mathematician and logician. He made major contributions to the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus. He died of starvation in a Czech prison camp in Prague in 1945. Life and career Gentzen was a student of Paul Bernays at the University of Göttingen. Bernays was fired as "non-Aryan" in April 1933 and therefore Hermann Weyl formally acted as his supervisor. Gentzen joined the Sturmabteilung in November 1933, although he was by no means compelled to do so. Nevertheless, he kept in contact with Bernays until the beginning of the Second World War. In 1935, he corresponded with Abraham Fraenkel in Jerusalem and was implicated by the Nazi teachers' union as one who "keeps contacts to the Chosen People." In 1935 and 1936, Hermann Weyl, head of the Göttingen mathematics department in 1933 until his resignation under Nazi pressure, made strong efforts t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning. This contrasts with Hilbert-style systems, which instead use axioms as much as possible to express the logical laws of deductive reasoning. History Natural deduction grew out of a context of dissatisfaction with the axiomatizations of deductive reasoning common to the systems of Hilbert, Frege, and Russell (see, e.g., Hilbert system). Such axiomatizations were most famously used by Russell and Whitehead in their mathematical treatise ''Principia Mathematica''. Spurred on by a series of seminars in Poland in 1926 by Łukasiewicz that advocated a more natural treatment of logic, Jaśkowski made the earliest attempts at defining a more natural deduction, first in 1929 using a diagrammatic notation, and later updating his proposal in a sequence of papers in 1934 and 1935. His proposals led to d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irving Copi
Irving Marmer Copi (; né Copilovich or Copilowish; July 28, 1917 – August 19, 2002) was an American philosopher, logician, and university textbook author. Biography Copi studied under Bertrand Russell while at the University of Chicago. In 1948 he contributed to the calculus of relations with his article using logical matrices. Copi taught at the University of Illinois, the United States Air Force Academy, Princeton University, and the Georgetown University Logic Institute, before teaching logic at the University of Michigan, 1958–69, and at the University of Hawaii at Manoa, 1969–90. Assigned to teach logic, Copi reviewed the available textbooks and decided to write his own. His manuscript was split into his ''Introduction to Logic'' (1953), and ''Symbolic Logic'' (1954). A reviewer noted that it had an "unusually comprehensive chapter on definition" and mentions that "the author accounts for the seductive nature of informal fallacies". The textbooks proved popular, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |