|
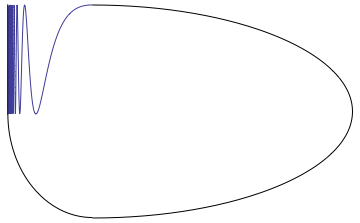
Topologist's Sine Curve
In the branch of mathematics known as topology, the topologist's sine curve or Warsaw sine curve is a topological space with several interesting properties that make it an important textbook example. It can be defined as the graph of the function sin(1/''x'') on the half-open interval (0, 1], together with the origin, under the topology subspace topology, induced from the Euclidean plane: : T = \left\ \cup \. Properties The topologist's sine curve ''T'' is connected but neither locally connected nor path connected. This is because it includes the point (0,0) but there is no way to link the function to the origin so as to make a path. The space ''T'' is the continuous image of a locally compact space (namely, let ''V'' be the space ∪ (0, 1], and use the map ''f'' from ''V'' to ''T'' defined by = (0,0) and = for ''x'' > 0), but ''T'' is not locally compact itself. The topological dimension of ''T'' is 1. Variants Two variants of the topologist's sine cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topologist's Sine Curve
In the branch of mathematics known as topology, the topologist's sine curve or Warsaw sine curve is a topological space with several interesting properties that make it an important textbook example. It can be defined as the graph of the function sin(1/''x'') on the half-open interval (0, 1], together with the origin, under the topology subspace topology, induced from the Euclidean plane: : T = \left\ \cup \. Properties The topologist's sine curve ''T'' is connected but neither locally connected nor path connected. This is because it includes the point (0,0) but there is no way to link the function to the origin so as to make a path. The space ''T'' is the continuous image of a locally compact space (namely, let ''V'' be the space ∪ (0, 1], and use the map ''f'' from ''V'' to ''T'' defined by = (0,0) and = for ''x'' > 0), but ''T'' is not locally compact itself. The topological dimension of ''T'' is 1. Variants Two variants of the topologist's sine cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Dimension
In mathematics, the Lebesgue covering dimension or topological dimension of a topological space is one of several different ways of defining the dimension of the space in a topological invariant, topologically invariant way. Informal discussion For ordinary Euclidean spaces, the Lebesgue covering dimension is just the ordinary Euclidean dimension: zero for points, one for lines, two for planes, and so on. However, not all topological spaces have this kind of "obvious" dimension, and so a precise definition is needed in such cases. The definition proceeds by examining what happens when the space is covered by open sets. In general, a topological space ''X'' can be open cover, covered by open sets, in that one can find a collection of open sets such that ''X'' lies inside of their union (set theory), union. The covering dimension is the smallest number ''n'' such that for every cover, there is a refinement (topology), refinement in which every point in ''X'' lies in the intersection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Counterexamples In Topology
''Counterexamples in Topology'' (1970, 2nd ed. 1978) is a book on mathematics by topologists Lynn Steen and J. Arthur Seebach, Jr. In the process of working on problems like the metrization problem, topologists (including Steen and Seebach) have defined a wide variety of topological properties. It is often useful in the study and understanding of abstracts such as topological spaces to determine that one property does not follow from another. One of the easiest ways of doing this is to find a counterexample which exhibits one property but not the other. In ''Counterexamples in Topology'', Steen and Seebach, together with five students in an undergraduate research project at St. Olaf College, Minnesota in the summer of 1967, canvassed the field of topology for such counterexamples and compiled them in an attempt to simplify the literature. For instance, an example of a first-countable space which is not second-countable is counterexample #3, the discrete topology on an uncoun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Warsaw Circle
Shape theory is a branch of topology that provides a more global view of the topological spaces than homotopy theory. The two coincide on compacta dominated homotopically by finite polyhedra. Shape theory associates with the Čech homology theory while homotopy theory associates with the singular homology theory. Background Shape theory was reinvented, further developed and promoted by the Polish mathematician Karol Borsuk in 1968. Actually, the name ''shape theory'' was coined by Borsuk. Warsaw Circle Borsuk lived and worked in Warsaw, hence the name of one of the fundamental examples of the area, the Warsaw circle. It is a compact subset of the plane produced by "closing up" a topologist's sine curve with an arc. The homotopy groups of the Warsaw circle are all trivial, just like those of a point, and so any map between the Warsaw circle and a point induces a weak homotopy equivalence. However these two spaces are not homotopy equivalent. So by the Whitehead theorem, the War ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Topologies
The following is a list of named topologies or topological spaces, many of which are counterexamples in topology and related branches of mathematics. This is not a list of properties that a topology or topological space might possess; for that, see List of general topology topics and Topological property. Widely known topologies * The Baire space − \N^ with the product topology, where \N denotes the natural numbers endowed with the discrete topology. It is the space of all sequences of natural numbers. * Cantor set − A subset of the closed interval , 1/math> with remarkable properties. ** Cantor dust * Discrete topology − All subsets are open. * Euclidean topology − The natural topology on Euclidean space \Reals^n induced by the Euclidean metric, which is itself induced by the Euclidean norm. ** Real line − \Reals ** Space-filling curve ** Unit interval − , 1/math> * Extended real number line * Hilbert cube − , 1/1\times , 1/2\times , 1/3\times \cdots with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Connected Space
In topology and other branches of mathematics, a topological space ''X'' is locally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets. Background Throughout the history of topology, connectedness and compactness have been two of the most widely studied topological properties. Indeed, the study of these properties even among subsets of Euclidean space, and the recognition of their independence from the particular form of the Euclidean metric, played a large role in clarifying the notion of a topological property and thus a topological space. However, whereas the structure of ''compact'' subsets of Euclidean space was understood quite early on via the Heine–Borel theorem, ''connected'' subsets of \R^n (for ''n'' > 1) proved to be much more complicated. Indeed, while any compact Hausdorff space is locally compact, a connected space—and even a connected subset of the Euclidean plane—need not be locally connected (see below). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Connected
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union (set theory), union of two or more disjoint set, disjoint Empty set, non-empty open (topology), open subsets. Connectedness is one of the principal topological properties that are used to distinguish topological spaces. A subset of a topological space X is a if it is a connected space when viewed as a Subspace topology, subspace of X. Some related but stronger conditions are #Path connectedness, path connected, Simply connected space, simply connected, and N-connected space, n-connected. Another related notion is ''Locally connected space, locally connected'', which neither implies nor follows from connectedness. Formal definition A topological space X is said to be if it is the union of two disjoint non-empty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", i.e. that the space not exclude any ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topologic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Point
In mathematics, a limit point, accumulation point, or cluster point of a set S in a topological space X is a point x that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. A limit point of a set S does not itself have to be an element of S. There is also a closely related concept for sequences. A cluster point or accumulation point of a sequence (x_n)_ in a topological space X is a point x such that, for every neighbourhood V of x, there are infinitely many natural numbers n such that x_n \in V. This definition of a cluster or accumulation point of a sequence generalizes to nets and filters. The similarly named notion of a (respectively, a limit point of a filter, a limit point of a net) by definition refers to a point that the sequence converges to (respectively, the filter converges to, the net converges to). Importantly, although "limit point of a set" is synon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Compact
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which every point has a compact neighborhood. In mathematical analysis locally compact spaces that are Hausdorff are of particular interest; they are abbreviated as LCH spaces. Formal definition Let ''X'' be a topological space. Most commonly ''X'' is called locally compact if every point ''x'' of ''X'' has a compact neighbourhood, i.e., there exists an open set ''U'' and a compact set ''K'', such that x\in U\subseteq K. There are other common definitions: They are all equivalent if ''X'' is a Hausdorff space (or preregular). But they are not equivalent in general: :1. every point of ''X'' has a compact neighbourhood. :2. every point of ''X'' has a closed compact neighbourhood. :2′. every point of ''X'' has a relatively compact neighbourhoo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |