|
Thomas Ranken Lyle Medal
The Thomas Ranken Lyle Medal is awarded at most every two years by the Australian Academy of Science to a mathematician or physicist for his or her outstanding research accomplishments.Thomas Ranken Lyle Medal , , retrieved 2010-06-06. It is named after , an Irish who became a professor at the |
Australian Academy Of Science
The Australian Academy of Science was founded in 1954 by a group of distinguished Australians, including Australian Fellows of the Royal Society of London. The first president was Sir Mark Oliphant. The academy is modelled after the Royal Society and operates under a Royal Charter; as such, it is an independent body, but it has government endorsement. The Academy Secretariat is in Canberra, at the Shine Dome. The objectives of the academy are to promote science and science education through a wide range of activities. It has defined four major program areas: :* Recognition of outstanding contributions to science :* Education and public awareness :* Science policy :* International relations The academy also runs the 22 National Committees for Science which provide a forum to discuss issues relevant to all the scientific disciplines in Australia. Origins The Australian National Research Council (ANRC) was established in 1919 for the purpose of representing Australia on the In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterated Function
In mathematics, an iterated function is a function (that is, a function from some set to itself) which is obtained by composing another function with itself a certain number of times. The process of repeatedly applying the same function is called iteration. In this process, starting from some initial object, the result of applying a given function is fed again in the function as input, and this process is repeated. For example on the image on the right: :with the circle‑shaped symbol of function composition. Iterated functions are objects of study in computer science, fractals, dynamical systems, mathematics and renormalization group physics. Definition The formal definition of an iterated function on a set ''X'' follows. Let be a set and be a function. Defining as the ''n''-th iterate of (a notation introduced by Hans Heinrich Bürmann and John Frederick William Herschel), where ''n'' is a non-negative integer, by: f^0 ~ \stackrel ~ \operatorname_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
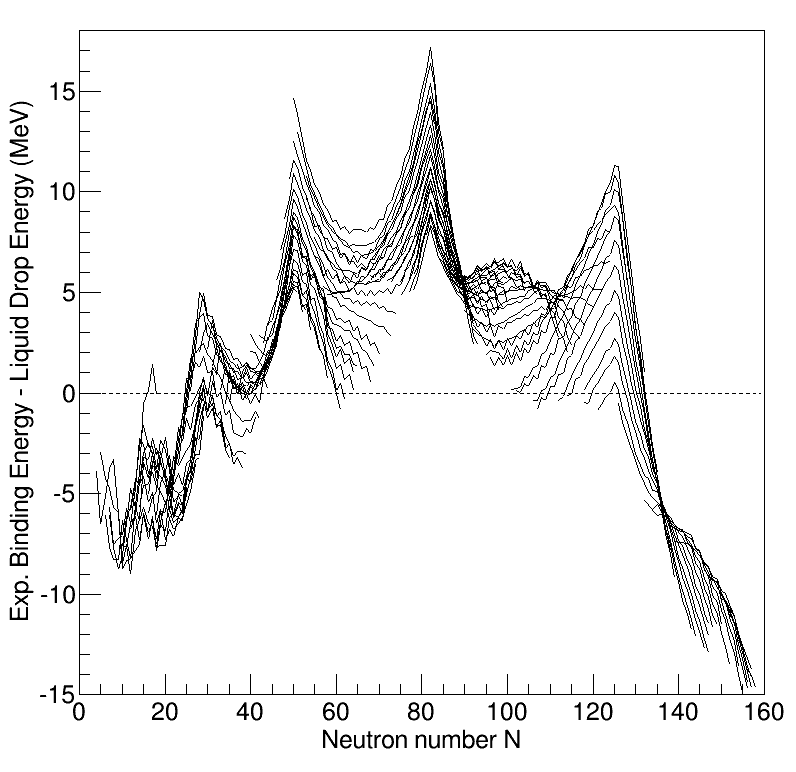
Nuclear Structure
Understanding the structure of the atomic nucleus is one of the central challenges in nuclear physics. Models The liquid drop model The liquid drop model is one of the first models of nuclear structure, proposed by Carl Friedrich von Weizsäcker in 1935. It describes the nucleus as a semiclassical fluid made up of neutrons and protons, with an internal repulsive electrostatic force proportional to the number of protons. The quantum mechanical nature of these particles appears via the Pauli exclusion principle, which states that no two nucleons of the same kind can be at the same state. Thus the fluid is actually what is known as a Fermi liquid. In this model, the binding energy of a nucleus with Z protons and N neutrons is given by :E_ = a_ A - a_ A^ - a_ \frac - a_ \frac - \delta(A,Z) where A=Z+N is the total number of nucleons (Mass Number). The terms proportional to A and A^ represent the volume and surface energy of the liquid drop, the term proportional to Z^ represents t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ian Sloan (mathematician)
Ian Hugh Sloan AO (born 17 June 1938, in Melbourne) is an Australian applied mathematician. He was educated at the University of Melbourne (BSc 1958, BA (hons) 1960), University of Adelaide (MSc, 1961) and University College London, where he was supervised by renowned mathematical physicist Sir Harrie Massey, and earned his PhD in 1964. He was a research scientist for the Colonial Sugar Refining company 1964–5, and since 1965 has been at the University of New South Wales, where he has been Scientia Professor since 1999. He served as Head of the School of Mathematics from 1986 to 1990 and from 1992 to 1993.Ian Sloan's web page maths.unsw.edu.au, retrieved 2012-05-11. His early work was in theoretical |
Nucleon
In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number (nucleon number). Until the 1960s, nucleons were thought to be elementary particles, not made up of smaller parts. Now they are known to be composite particles, made of three quarks bound together by the strong interaction. The interaction between two or more nucleons is called internucleon interaction or nuclear force, which is also ultimately caused by the strong interaction. (Before the discovery of quarks, the term "strong interaction" referred to just internucleon interactions.) Nucleons sit at the boundary where particle physics and nuclear physics overlap. Particle physics, particularly quantum chromodynamics, provides the fundamental equations that describe the properties of quarks and of the strong interaction. These equations describe quantitatively how quarks can bind toget ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quark
A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly observable matter is composed of up quarks, down quarks and electrons. Owing to a phenomenon known as ''color confinement'', quarks are never found in isolation; they can be found only within hadrons, which include baryons (such as protons and neutrons) and mesons, or in quark–gluon plasmas. There is also the theoretical possibility of more exotic phases of quark matter. For this reason, much of what is known about quarks has been drawn from observations of hadrons. Quarks have various intrinsic properties, including electric charge, mass, color charge, and spin. They are the only elementary particles in the Standard Model of particle physics to experience all four fundamental interactions, also known as ''fundamental forces'' (electro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martingale Central Limit Theorem
In probability theory, the central limit theorem says that, under certain conditions, the sum of many independent identically-distributed random variables, when scaled appropriately, converges in distribution to a standard normal distribution. The martingale central limit theorem generalizes this result for random variables to martingales, which are stochastic processes where the change in the value of the process from time ''t'' to time ''t'' + 1 has expectation zero, even conditioned on previous outcomes. Statement Here is a simple version of the martingale central limit theorem: Let X_1, X_2, \dots\, be a martingale with bounded increments; that is, suppose :\operatorname _ - X_t \vert X_1,\dots, X_t0\,, and :, X_ - X_t, \le k almost surely In probability theory, an event is said to happen almost surely (sometimes abbreviated as a.s.) if it happens with probability 1 (or Lebesgue measure 1). In other words, the set of possible exceptions may be non-empty, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Process
In mathematics and statistics, a stationary process (or a strict/strictly stationary process or strong/strongly stationary process) is a stochastic process whose unconditional joint probability distribution does not change when shifted in time. Consequently, parameters such as mean and variance also do not change over time. If you draw a line through the middle of a stationary process then it should be flat; it may have 'seasonal' cycles, but overall it does not trend up nor down. Since stationarity is an assumption underlying many statistical procedures used in time series analysis, non-stationary data are often transformed to become stationary. The most common cause of violation of stationarity is a trend in the mean, which can be due either to the presence of a unit root or of a deterministic trend. In the former case of a unit root, stochastic shocks have permanent effects, and the process is not mean-reverting. In the latter case of a deterministic trend, the process is called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radio Astronomy
Radio astronomy is a subfield of astronomy that studies celestial objects at radio frequencies. The first detection of radio waves from an astronomical object was in 1933, when Karl Jansky at Bell Telephone Laboratories reported radiation coming from the Milky Way. Subsequent observations have identified a number of different sources of radio emission. These include stars and galaxies, as well as entirely new classes of objects, such as radio galaxies, quasars, pulsars, and masers. The discovery of the cosmic microwave background radiation, regarded as evidence for the Big Bang theory, was made through radio astronomy. Radio astronomy is conducted using large radio antennas referred to as radio telescopes, that are either used singularly, or with multiple linked telescopes utilizing the techniques of radio interferometry and aperture synthesis. The use of interferometry allows radio astronomy to achieve high angular resolution, as the resolving power of an interferometer is set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematics
Kinematics is a subfield of physics, developed in classical mechanics, that describes the Motion (physics), motion of points, Physical object, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics (physics), kinetics, not kinematics. For further details, see analytical dynamics. Kinematics is used in astrophysics to describe the motion of celestial bodies and collections of such bodies. In mechanical engin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |