|
Term Rewriting System
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or reduction systems). In their most basic form, they consist of a set of objects, plus relations on how to transform those objects. Rewriting can be non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several theorem provers and declarative programming languages are based on term rewriting. Example cases Logic In logic, the procedure for obtaining the conjunctive normal form (CNF) of a formula can be implemented as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Term (logic)
In mathematical logic, a term denotes a mathematical object while a formula denotes a mathematical fact. In particular, terms appear as components of a formula. This is analogous to natural language, where a noun phrase refers to an object and a whole sentence refers to a fact. A first-order term is recursively constructed from constant symbols, variables and function symbols. An expression formed by applying a predicate symbol to an appropriate number of terms is called an atomic formula, which evaluates to true or false in bivalent logics, given an interpretation. For example, is a term built from the constant 1, the variable , and the binary function symbols and ; it is part of the atomic formula which evaluates to true for each real-numbered value of . Besides in logic, terms play important roles in universal algebra, and rewriting systems. Formal definition Given a set ''V'' of variable symbols, a set ''C'' of constant symbols and sets ''F''''n'' of ''n''-ary fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Closure
In mathematics, the symmetric closure of a binary relation R on a set X is the smallest symmetric relation on X that contains R. For example, if X is a set of airports and xRy means "there is a direct flight from airport x to airport y", then the symmetric closure of R is the relation "there is a direct flight either from x to y or from y to x". Or, if X is the set of humans and R is the relation 'parent of', then the symmetric closure of R is the relation "x is a parent or a child of y". Definition The symmetric closure S of a relation R on a set X is given by S = R \cup \. In other words, the symmetric closure of R is the union of R with its converse relation, R^. See also * * {{annotated link, Reflexive closure References * Franz Baader and Tobias Nipkow Tobias Nipkow (born 1958) is a German computer scientist. Career Nipkow received his Diplom (MSc) in computer science from the Department of Computer Science of the Technische Hochschule Darmstadt in 1982, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflexive Transitive Closure
In mathematics, a subset of a given set is closed under an operation of the larger set if performing that operation on members of the subset always produces a member of that subset. For example, the natural numbers are closed under addition, but not under subtraction: is not a natural number, although both 1 and 2 are. Similarly, a subset is said to be closed under a ''collection'' of operations if it is closed under each of the operations individually. The closure of a subset is the result of a closure operator applied to the subset. The ''closure'' of a subset under some operations is the smallest subset that is closed under these operations. It is often called the ''span'' (for example linear span) or the ''generated set''. Definitions Let be a set equipped with one or several methods for producing elements of from other elements of . Operations and (partial) multivariate function are examples of such methods. If is a topological space, the limit of a sequence of elemen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Relation
In mathematics, a binary relation associates elements of one set, called the ''domain'', with elements of another set, called the ''codomain''. A binary relation over Set (mathematics), sets and is a new set of ordered pairs consisting of elements in and in . It is a generalization of the more widely understood idea of a unary function. It encodes the common concept of relation: an element is ''related'' to an element , if and only if the pair belongs to the set of ordered pairs that defines the ''binary relation''. A binary relation is the most studied special case of an Finitary relation, -ary relation over sets , which is a subset of the Cartesian product X_1 \times \cdots \times X_n. An example of a binary relation is the "divides" relation over the set of prime numbers \mathbb and the set of integers \mathbb, in which each prime is related to each integer that is a Divisibility, multiple of , but not to an integer that is not a multiple of . In this relation, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
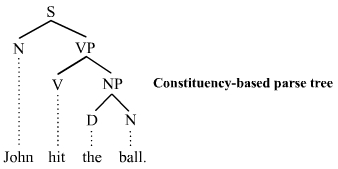
Verb Phrase
In linguistics, a verb phrase (VP) is a syntactic unit composed of a verb and its arguments except the subject of an independent clause or coordinate clause. Thus, in the sentence ''A fat man quickly put the money into the box'', the words ''quickly put the money into the box'' constitute a verb phrase; it consists of the verb ''put'' and its arguments, but not the subject ''a fat man''. A verb phrase is similar to what is considered a ''predicate'' in traditional grammars. Verb phrases generally are divided among two types: finite, of which the head of the phrase is a finite verb; and nonfinite, where the head is a nonfinite verb, such as an infinitive, participle or gerund. Phrase structure grammars acknowledge both types, but dependency grammars treat the subject as just another verbal dependent, and they do not recognize the finite verbal phrase constituent. Understanding verb phrase analysis depends on knowing which theory applies in context. In phrase structure grammars In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morpheme
A morpheme is the smallest meaningful Constituent (linguistics), constituent of a linguistic expression. The field of linguistics, linguistic study dedicated to morphemes is called morphology (linguistics), morphology. In English, morphemes are often but bound and free morphemes, not necessarily word, words. Morphemes that stand alone are considered root (linguistics), roots (such as the morpheme ''cat''); other morphemes, called affix, affixes, are found only in combination with other morphemes. For example, the ''-s'' in ''cats'' indicates the concept of plurality but is always bound to another concept to indicate a specific kind of plurality. This distinction is not universal and does not apply to, for example, Latin, in which many roots cannot stand alone. For instance, the Latin root ''reg-'' (‘king’) must always be suffixed with a case marker: ''rex'' (''reg-s''), ''reg-is'', ''reg-i'', etc. For a language like Latin, a root can be defined as the main lexical morpheme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sentence (linguistics)
In linguistics and grammar, a sentence is a linguistic expression, such as the English example "The quick brown fox jumps over the lazy dog." In traditional grammar, it is typically defined as a string of words that expresses a complete thought, or as a unit consisting of a subject and predicate. In non-functional linguistics it is typically defined as a maximal unit of syntactic structure such as a constituent. In functional linguistics, it is defined as a unit of written texts delimited by graphological features such as upper-case letters and markers such as periods, question marks, and exclamation marks. This notion contrasts with a curve, which is delimited by phonologic features such as pitch and loudness and markers such as pauses; and with a clause, which is a sequence of words that represents some process going on throughout time. A sentence can include words grouped meaningfully to express a statement, question, exclamation, request, command, or suggestion. Typical a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noun Phrase
In linguistics, a noun phrase, or nominal (phrase), is a phrase that has a noun or pronoun as its head or performs the same grammatical function as a noun. Noun phrases are very common cross-linguistically, and they may be the most frequently occurring phrase type. Noun phrases often function as verb subjects and objects, as predicative expressions and as the complements of prepositions. Noun phrases can be embedded inside each other; for instance, the noun phrase ''some of his constituents'' contains the shorter noun phrase ''his constituents''. In some more modern theories of grammar, noun phrases with determiners are analyzed as having the determiner as the head of the phrase, see for instance Chomsky (1995) and Hudson (1990). Identification Some examples of noun phrases are underlined in the sentences below. The head noun appears in bold. ::This election-year's politics are annoying for many people. ::Almost every sentence contains at least one noun phrase. ::Current ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntactic Category
A syntactic category is a syntactic unit that theories of syntax assume. Word classes, largely corresponding to traditional parts of speech (e.g. noun, verb, preposition, etc.), are syntactic categories. In phrase structure grammars, the ''phrasal categories'' (e.g. noun phrase, verb phrase, prepositional phrase, etc.) are also syntactic categories. Dependency grammars, however, do not acknowledge phrasal categories (at least not in the traditional sense). Word classes considered as syntactic categories may be called ''lexical categories'', as distinct from phrasal categories. The terminology is somewhat inconsistent between the theoretical models of different linguists. However, many grammars also draw a distinction between ''lexical categories'' (which tend to consist of content words, or phrases headed by them) and ''functional categories'' (which tend to consist of function words or abstract functional elements, or phrases headed by them). The term ''lexical category'' therefore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generative Grammar
Generative grammar, or generativism , is a linguistic theory that regards linguistics as the study of a hypothesised innate grammatical structure. It is a biological or biologistic modification of earlier structuralist theories of linguistics, deriving ultimately from glossematics. Generative grammar considers grammar as a system of rules that generates exactly those combinations of words that form grammatical sentences in a given language. It is a system of explicit rules that may apply repeatedly to generate an indefinite number of sentences which can be as long as one wants them to be. The difference from structural and functional models is that the object is base-generated within the verb phrase in generative grammar. This purportedly cognitive structure is thought of as being a part of a universal grammar, a syntactic structure which is caused by a genetic mutation in humans. Generativists have created numerous theories to make the NP VP (NP) analysis work in natural la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
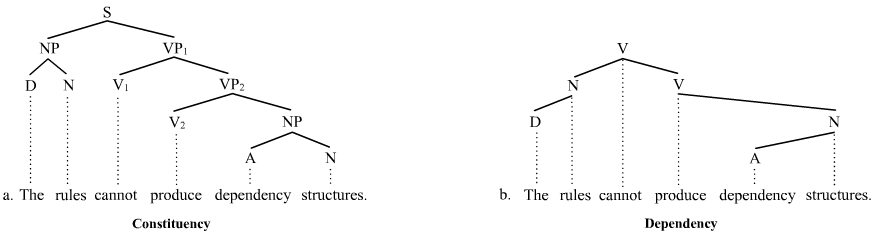
Phrase Structure Rule
Phrase structure rules are a type of rewrite rule used to describe a given language's syntax and are closely associated with the early stages of transformational grammar, proposed by Noam Chomsky in 1957. They are used to break down a natural language sentence into its constituent parts, also known as syntactic categories, including both lexical categories (parts of speech) and phrasal categories. A grammar that uses phrase structure rules is a type of phrase structure grammar. Phrase structure rules as they are commonly employed operate according to the constituency relation, and a grammar that employs phrase structure rules is therefore a ''constituency grammar''; as such, it stands in contrast to ''dependency grammars'', which are based on the dependency relation. Definition and examples Phrase structure rules are usually of the following form: :A \to B \quad C meaning that the constituent A is separated into the two subconstituents B and C. Some examples for English are a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |