|
Tensor Product Of Algebras
In mathematics, the tensor product of two algebras over a commutative ring ''R'' is also an ''R''-algebra. This gives the tensor product of algebras. When the ring is a field, the most common application of such products is to describe the product of algebra representations. Definition Let ''R'' be a commutative ring and let ''A'' and ''B'' be ''R''-algebras. Since ''A'' and ''B'' may both be regarded as ''R''-modules, their tensor product :A \otimes_R B is also an ''R''-module. The tensor product can be given the structure of a ring by defining the product on elements of the form by :(a_1\otimes b_1)(a_2\otimes b_2) = a_1 a_2\otimes b_1b_2 and then extending by linearity to all of . This ring is an ''R''-algebra, associative and unital with identity element given by . where 1''A'' and 1''B'' are the identity elements of ''A'' and ''B''. If ''A'' and ''B'' are commutative, then the tensor product is commutative as well. The tensor product turns the category of ''R''-algebras ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros. The fundamental objects of study in algebraic geometry are algebraic varieties, which are geometric manifestations of solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are: plane algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscates and Cassini ovals. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of the points of special interest like the singular points, the inflection points and the points at infinity. More advanced questions involve the topology of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebras
In mathematics, an algebra over a field (often simply called an algebra) is a vector space equipped with a bilinear product. Thus, an algebra is an algebraic structure consisting of a set together with operations of multiplication and addition and scalar multiplication by elements of a field and satisfying the axioms implied by "vector space" and "bilinear". The multiplication operation in an algebra may or may not be associative, leading to the notions of associative algebras and non-associative algebras. Given an integer ''n'', the ring of real square matrices of order ''n'' is an example of an associative algebra over the field of real numbers under matrix addition and matrix multiplication since matrix multiplication is associative. Three-dimensional Euclidean space with multiplication given by the vector cross product is an example of a nonassociative algebra over the field of real numbers since the vector cross product is nonassociative, satisfying the Jacobi identity inste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
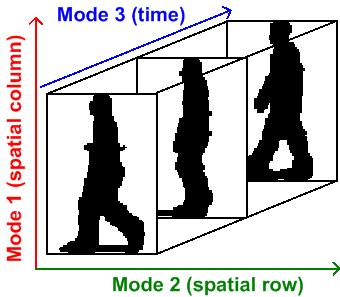
Multilinear Subspace Learning
Multilinear subspace learning is an approach to dimensionality reduction.M. A. O. Vasilescu, D. Terzopoulos (2003"Multilinear Subspace Analysis of Image Ensembles" "Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’03), Madison, WI, June, 2003"M. A. O. Vasilescu, D. Terzopoulos (2002"Multilinear Analysis of Image Ensembles: TensorFaces" Proc. 7th European Conference on Computer Vision (ECCV'02), Copenhagen, Denmark, May, 2002M. A. O. Vasilescu,(2002"Human Motion Signatures: Analysis, Synthesis, Recognition" "Proceedings of International Conference on Pattern Recognition (ICPR 2002), Vol. 3, Quebec City, Canada, Aug, 2002, 456–460." Dimension reduction, Dimensionality reduction can be performed on a data tensor that contains a collection of observations have been vectorized, or observations that are treated as matrices and concatenated into a data tensor.X. He, D. Cai, P. NiyogiTensor subspace analysis in: Advances in Neural Information Proce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearly Disjoint
In mathematics, algebras ''A'', ''B'' over a field ''k'' inside some field extension \Omega of ''k'' are said to be linearly disjoint over ''k'' if the following equivalent conditions are met: *(i) The map A \otimes_k B \to AB induced by (x, y) \mapsto xy is injective. *(ii) Any ''k''-basis of ''A'' remains linearly independent over ''B''. *(iii) If u_i, v_j are ''k''-bases for ''A'', ''B'', then the products u_i v_j are linearly independent over ''k''. Note that, since every subalgebra of \Omega is a domain, (i) implies A \otimes_k B is a domain (in particular reduced). Conversely if ''A'' and ''B'' are fields and either ''A'' or ''B'' is an algebraic extension of ''k'' and A \otimes_k B is a domain then it is a field and ''A'' and ''B'' are linearly disjoint. However, there are examples where A \otimes_k B is a domain but ''A'' and ''B'' are not linearly disjoint: for example, ''A'' = ''B'' = ''k''(''t''), the field of rational functions over ''k''. One also has: ''A'', ''B'' are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Product Of Fields
In mathematics, the tensor product of two fields is their tensor product as algebras over a common subfield. If no subfield is explicitly specified, the two fields must have the same characteristic and the common subfield is their prime subfield. The tensor product of two fields is sometimes a field, and often a direct product of fields; In some cases, it can contain non-zero nilpotent elements. The tensor product of two fields expresses in a single structure the different way to embed the two fields in a common extension field. Compositum of fields First, one defines the notion of the compositum of fields. This construction occurs frequently in field theory. The idea behind the compositum is to make the smallest field containing two other fields. In order to formally define the compositum, one must first specify a tower of fields. Let ''k'' be a field and ''L'' and ''K'' be two extensions of ''k''. The compositum, denoted ''K.L'', is defined to be K.L = k(K \cup L) where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Product Of Modules
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps (e.g. multiplication) to be carried out in terms of linear maps. The module construction is analogous to the construction of the tensor product of vector spaces, but can be carried out for a pair of modules over a commutative ring resulting in a third module, and also for a pair of a right-module and a left-module over any ring, with result an abelian group. Tensor products are important in areas of abstract algebra, homological algebra, algebraic topology, algebraic geometry, operator algebras and noncommutative geometry. The universal property of the tensor product of vector spaces extends to more general situations in abstract algebra. It allows the study of bilinear or multilinear operations via linear operations. The tensor product of an algebra and a module can be used for extension of scalars. For a commutative ring, the tensor product of modules can be iterated to form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extension Of Scalars
In algebra, given a ring homomorphism f: R \to S, there are three ways to change the coefficient ring of a module; namely, for a left ''R''-module ''M'' and a left ''S''-module ''N'', *f_! M = S\otimes_R M, the induced module. *f_* M = \operatorname_R(S, M), the coinduced module. *f^* N = N_R, the restriction of scalars. They are related as adjoint functors: :f_! : \text_R \leftrightarrows \text_S : f^* and :f^* : \text_S \leftrightarrows \text_R : f_*. This is related to Shapiro's lemma. Operations Restriction of scalars Throughout this section, let R and S be two rings (they may or may not be commutative, or contain an identity), and let f:R \to S be a homomorphism. Restriction of scalars changes ''S''-modules into ''R''-modules. In algebraic geometry, the term "restriction of scalars" is often used as a synonym for Weil restriction. Definition Suppose that M is a module over S. Then it can be regarded as a module over R where the action of R is given via : \begin M\ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσος ''isos'' "equal", and μορφή ''morphe'' "form" or "shape". The interest in isomorphisms lies in the fact that two isomorphic objects have the same properties (excluding further information such as additional structure or names of objects). Thus isomorphic structures cannot be distinguished from the point of view of structure only, and may be identified. In mathematical jargon, one says that two objects are . An automorphism is an isomorphism from a structure to itself. An isomorphism between two structures is a canonical isomorphism (a canonical map that is an isomorphism) if there is only one isomorphism between the two structures (as it is the case for solutions of a univer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiber Product
In category theory, a branch of mathematics, a pullback (also called a fiber product, fibre product, fibered product or Cartesian square) is the limit of a diagram consisting of two morphisms and with a common codomain. The pullback is often written : and comes equipped with two natural morphisms and . The pullback of two morphisms and need not exist, but if it does, it is essentially uniquely defined by the two morphisms. In many situations, may intuitively be thought of as consisting of pairs of elements with in , in , and . For the general definition, a universal property is used, which essentially expresses the fact that the pullback is the "most general" way to complete the two given morphisms to a commutative square. The dual concept of the pullback is the ''pushout''. Universal property Explicitly, a pullback of the morphisms and consists of an object and two morphisms and for which the diagram : commutes. Moreover, the pullback must be universal wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. More generally, an algebraic curve is an algebraic variety of dimension one. Equivalently, an algebraic curve is an algebraic variety that is birationally equivalent to an algebraic plane curve. If the curve is contained in an affine space or a projective space, one can take a projection for such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scheme (mathematics)
In mathematics, a scheme is a mathematical structure that enlarges the notion of algebraic variety in several ways, such as taking account of multiplicities (the equations ''x'' = 0 and ''x''2 = 0 define the same algebraic variety but different schemes) and allowing "varieties" defined over any commutative ring (for example, Fermat curves are defined over the integers). Scheme theory was introduced by Alexander Grothendieck in 1960 in his treatise "Éléments de géométrie algébrique"; one of its aims was developing the formalism needed to solve deep problems of algebraic geometry, such as the Weil conjectures (the last of which was proved by Pierre Deligne). Strongly based on commutative algebra, scheme theory allows a systematic use of methods of topology and homological algebra. Scheme theory also unifies algebraic geometry with much of number theory, which eventually led to Wiles's proof of Fermat's Last Theorem. Formally, a scheme is a topological space together with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |