|
Temporal Discretization
In applied physics and engineering, temporal discretization is a mathematical technique for solving transient problems, such as flow problems. Transient problems are often solved using computer-aided engineering (CAE) simulations, which require discretizing the governing equations in both space and time. Temporal discretization involves the integration of every term in various equations over a time step (\Delta t). The spatial domain can be discretized to produce a semi-discrete form: \frac(x,t) = F(\varphi).~ The first-order temporal discretization using backward differences is \frac = F(\varphi), And the second-order discretization is \frac = F(\varphi), where * \varphi is a scalar * n + 1 is the value at the next time, t + \Delta t * n is the value at the current time, t * n - 1 is the value at the previous time, t - \Delta t The function F(\varphi) is evaluated using implicit- and explicit-time integration. Description Temporal discretization is done by in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Applied Physics
Applied physics is the application of physics to solve scientific or engineering problems. It is usually considered a bridge or a connection between physics and engineering. "Applied" is distinguished from "pure" by a subtle combination of factors, such as the motivation and attitude of researchers and the nature of the relationship to the technology or science that may be affected by the work. Applied physics is rooted in the fundamental truths and basic concepts of the physical sciences but is concerned with the utilization of scientific principles in practical devices and systems and with the application of physics in other areas of science and high technology. Examples of research and development areas * Accelerator physics *Acoustics * Atmospheric physics *Biophysics * Brain–computer interfacing *Chemistry * Chemical physics * Differentiable programming **Artificial intelligence ** Scientific computing *Engineering physics **Chemical engineering **Electrical engineeri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Crank–Nicolson Method
In numerical analysis, the Crank–Nicolson method is a finite difference method used for numerically solving the heat equation and similar partial differential equations. It is a Big O notation, second-order method in time. It is Explicit and implicit methods, implicit in time, can be written as an implicit Runge–Kutta method, and it is Numerical stability, numerically stable. The method was developed by John Crank and Phyllis Nicolson in the 1940s. For diffusion equations (and many other equations), it can be shown the Crank–Nicolson method is unconditionally Numerical stability, stable. However, the approximate solutions can still contain (decaying) spurious oscillations if the ratio of time step \Delta t times the thermal diffusivity to the square of space step, \Delta x^2, is large (typically, larger than 1/2 per Von Neumann stability analysis). For this reason, whenever large time steps or high spatial resolution is necessary, the less accurate backward Euler method is o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Finite Element Method
Finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. Computers are usually used to perform the calculations required. With high-speed supercomputers, better solutions can be achieved and are often required to solve the largest and most complex problems. FEM is a general numerical method for solving partial differential equations in two- or three-space variables (i.e., some boundary value problems). There are also studies about using FEM to solve high-dimensional problems. To solve a problem, FEM subdivides a large system into smaller, simpler parts called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Von Neumann Stability Analysis
In numerical analysis, von Neumann stability analysis (also known as Fourier stability analysis) is a procedure used to check the stability of finite difference schemes as applied to linear partial differential equations. The analysis is based on the Fourier decomposition of numerical error and was developed at Los Alamos National Laboratory after having been briefly described in a 1947 article by British researchers John Crank and Phyllis Nicolson. This method is an example of explicit time integration where the function that defines governing equation is evaluated at the current time. Later, the method was given a more rigorous treatment in an article co-authored by John von Neumann. Numerical stability The stability of numerical schemes is closely associated with numerical error. A finite difference scheme is stable if the errors made at one time step of the calculation do not cause the errors to be magnified as the computations are continued. A ''neutrally stable scheme'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lax–Wendroff Method
The Lax–Wendroff method, named after Peter Lax and Burton Wendroff, is a numerical method for the solution of hyperbolic partial differential equations, based on finite difference A finite difference is a mathematical expression of the form . Finite differences (or the associated difference quotients) are often used as approximations of derivatives, such as in numerical differentiation. The difference operator, commonly d ...s. It is second-order accurate in both space and time. This method is an example of explicit time integration where the function that defines the governing equation is evaluated at the current time. Definition Suppose one has an equation of the following form: \frac + \frac = 0 where and are independent variables, and the initial state, is given. Linear case In the linear case, where , and is a constant, u_i^ = u_i^n - \frac A\left u_^ - u_^ \right+ \frac A^2\left u_^ -2 u_^ + u_^ \right Here n refers to the t dimension and i refers to the x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Courant–Friedrichs–Lewy Condition
In mathematics, the convergence condition by Courant–Friedrichs–Lewy (CFL) is a necessary condition for convergence while solving certain partial differential equations (usually hyperbolic PDEs) numerically. It arises in the numerical analysis of explicit time integration schemes, when these are used for the numerical solution. As a consequence, the time step must be less than a certain upper bound, given a fixed spatial increment, in many explicit time-marching computer simulations; otherwise, the simulation produces incorrect or unstable results. The condition is named after Richard Courant, Kurt Friedrichs, and Hans Lewy who described it in their 1928 paper. Heuristic description The principle behind the condition is that, for example, if a wave is moving across a discrete spatial grid and we want to compute its amplitude at discrete time steps of equal duration, then this duration must be less than the time for the wave to travel to adjacent grid points. As a corollary, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Current Source
A current source is an electronic circuit that delivers or absorbs an electric current which is independent of the voltage across it. A current source is the dual of a voltage source. The term ''current sink'' is sometimes used for sources fed from a negative voltage supply. Figure 1 shows the schematic symbol for an ideal current source driving a resistive load. There are two types. An ''independent current source'' (or sink) delivers a constant current. A ''dependent current source'' delivers a current which is proportional to some other voltage or current in the circuit. Background , - align="center" , style="padding: 1em 2em 0;", , style="padding: 1em 2em 0;", , - align="center" , Voltage source , Current source , - align="center" , style="padding: 1em 2em 0;", , style="padding: 1em 2em 0;", , - align="center" , Controlled voltage source , Controlled current source , - align="center" , style="padding: 1em 2em 0;", , style="padding: 1em 2em 0;", , - align=" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
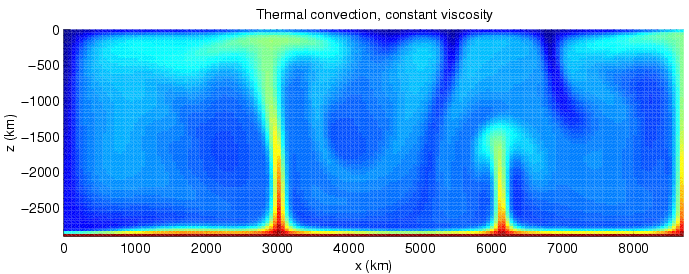
Convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be Transient state, transient (such as when a Multiphasic liquid, multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to Gravity, gravitational, Electromagnetism, electromagnetic or Fictitious force, fictitious body forces. Convection (heat transfer), Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its Earth's mantle, mantle. Discrete convective cells in the atmosphere can be identified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing. The concept of diffusion is widely used in many fields, including physics (Molecular diffusion, particle diffusion), chemistry, biology, sociology, economics, statistics, data science, and finance (diffusion of people, ideas, data and price v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Explicit And Implicit Methods
Explicit and implicit methods are approaches used in numerical analysis for obtaining numerical approximations to the solutions of time-dependent ordinary differential equation, ordinary and partial differential equations, as is required in computer simulations of Process (science), physical processes. ''Explicit methods'' calculate the state of a system at a later time from the state of the system at the current time, while ''implicit methods'' find a solution by solving an equation involving both the current state of the system and the later one. Mathematically, if Y(t) is the current system state and Y(t+\Delta t) is the state at the later time (\Delta t is a small time step), then, for an explicit method : Y(t+\Delta t) = F(Y(t))\, while for an implicit method one solves an equation : G\Big(Y(t), Y(t+\Delta t)\Big)=0 \qquad (1)\, to find Y(t+\Delta t). Computation Implicit methods require an extra computation (solving the above equation), and they can be much harder to impl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, systems. Modern engineering comprises many subfields which include designing and improving infrastructure, machinery, vehicles, electronics, Materials engineering, materials, and energy systems. The Academic discipline, discipline of engineering encompasses a broad range of more Academic specialization, specialized fields of engineering, each with a more specific emphasis for applications of applied mathematics, mathematics and applied science, science. See glossary of engineering. The word '':wikt:engineering, engineering'' is derived from the Latin . Definition The American Engineers' Council for Professional Development (the predecessor of the Accreditation Board for Engineering and Technology aka ABET) has defined "engineering" as: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |