|
Tukey's Test Of Additivity
In statistics, Tukey's test of additivity, named for John Tukey, is an approach used in two-way ANOVA ( regression analysis involving two qualitative factors) to assess whether the factor variables ( categorical variables) are additively related to the expected value of the response variable. It can be applied when there are no replicated values in the data set, a situation in which it is impossible to directly estimate a fully general non-additive regression structure and still have information left to estimate the error variance. The test statistic proposed by Tukey has one degree of freedom under the null hypothesis, hence this is often called "Tukey's one-degree-of-freedom test." Introduction The most common setting for Tukey's test of additivity is a two-way factorial analysis of variance (ANOVA) with one observation per cell. The response variable ''Y''''ij'' is observed in a table of cells with the rows indexed by ''i'' = 1,..., ''m'' and the columns indexed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Tukey
John Wilder Tukey (; June 16, 1915 – July 26, 2000) was an American mathematician and statistician, best known for the development of the fast Fourier Transform (FFT) algorithm and box plot. The Tukey range test, the Tukey lambda distribution, the Tukey test of additivity, and the Teichmüller–Tukey lemma all bear his name. He is also credited with coining the term '' bit'' and the first published use of the word ''software''. Biography Tukey was born in New Bedford, Massachusetts, in 1915, to a Latin teacher father and a private tutor. He was mainly taught by his mother and attended regular classes only for certain subjects like French. Tukey obtained a B.A. in 1936 and M.S. in 1937 in chemistry, from Brown University, before moving to Princeton University, where in 1939 he received a PhD in mathematics after completing a doctoral dissertation titled "On denumerability in topology". During World War II, Tukey worked at the Fire Control Research Office and coll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Variable
In statistics, a categorical variable (also called qualitative variable) is a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or nominal category on the basis of some qualitative property. In computer science and some branches of mathematics, categorical variables are referred to as enumerations or enumerated types. Commonly (though not in this article), each of the possible values of a categorical variable is referred to as a level. The probability distribution associated with a random categorical variable is called a categorical distribution. Categorical data is the statistical data type consisting of categorical variables or of data that has been converted into that form, for example as grouped data. More specifically, categorical data may derive from observations made of qualitative data that are summarised as counts or cross tabulations, or from observat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
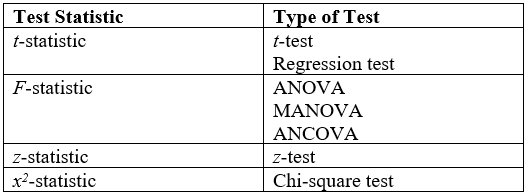
Test Statistic
Test statistic is a quantity derived from the sample for statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis. An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows ''p''-values to be calculated. A ''test statistic'' shares some of the same qualities of a descriptive stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a family of statistical methods used to compare the Mean, means of two or more groups by analyzing variance. Specifically, ANOVA compares the amount of variation ''between'' the group means to the amount of variation ''within'' each group. If the between-group variation is substantially larger than the within-group variation, it suggests that the group means are likely different. This comparison is done using an F-test. The underlying principle of ANOVA is based on the law of total variance, which states that the total variance in a dataset can be broken down into components attributable to different sources. In the case of ANOVA, these sources are the variation between groups and the variation within groups. ANOVA was developed by the statistician Ronald Fisher. In its simplest form, it provides a statistical test of whether two or more population means are equal, and therefore generalizes the Student's t-test#Independent two-sample t-test, ''t''- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Additive Model
In statistics, an additive model (AM) is a nonparametric regression method. It was suggested by Jerome H. Friedman and Werner Stuetzle (1981) and is an essential part of the ACE algorithm. The ''AM'' uses a one-dimensional smoother to build a restricted class of nonparametric regression models. Because of this, it is less affected by the curse of dimensionality than a ''p''-dimensional smoother. Furthermore, the ''AM'' is more flexible than a standard linear model, while being more interpretable than a general regression surface at the cost of approximation errors. Problems with ''AM'', like many other machine-learning methods, include model selection, overfitting, and multicollinearity. Description Given a data set \_^n of ''n'' statistical units, where \_^n represent predictors and y_i is the outcome, the ''additive model'' takes the form : \mathrm x_, \ldots, x_= \beta_0+\sum_^p f_j(x_) or : Y= \beta_0+\sum_^p f_j(X_)+\varepsilon Where \mathrm \epsilon = 0, \mathrm(\e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-distribution
In probability theory and statistics, the ''F''-distribution or ''F''-ratio, also known as Snedecor's ''F'' distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor), is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other ''F''-tests. Definitions The ''F''-distribution with ''d''1 and ''d''2 degrees of freedom is the distribution of X = \frac where U_1 and U_2 are independent random variables with chi-square distributions with respective degrees of freedom d_1 and d_2. It can be shown to follow that the probability density function (pdf) for ''X'' is given by \begin f(x; d_1,d_2) &= \frac \\ pt&=\frac \left(\frac\right)^ x^ \left(1+\frac \, x \right)^ \end for real ''x'' > 0. Here \mathrm is the beta function. In many applications, the parameters ''d''1 and ''d''2 are positive integers, but the distribution is wel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tukey's Range Test
Tukey's range test, also known as Tukey's test, Tukey method, Tukey's honest significance test, or Tukey's HSD (honestly significant difference) test, : Also occasionally described as "honestly", see e.g. is a single-step multiple comparison procedure and statistical test. It can be used to correctly interpret the statistical significance of the difference between means that have been selected for comparison because of their extreme values. The method was initially developed and introduced by John Tukey for use in Analysis of Variance (ANOVA), and usually has only been taught in connection with ANOVA. However, the studentized range distribution used to determine the level of significance of the differences considered in Tukey's test has vastly broader application: It is useful for researchers who have searched their collected data for remarkable differences between groups, but then cannot validly determine how significant their discovered stand-out difference is using standar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a family of statistical methods used to compare the Mean, means of two or more groups by analyzing variance. Specifically, ANOVA compares the amount of variation ''between'' the group means to the amount of variation ''within'' each group. If the between-group variation is substantially larger than the within-group variation, it suggests that the group means are likely different. This comparison is done using an F-test. The underlying principle of ANOVA is based on the law of total variance, which states that the total variance in a dataset can be broken down into components attributable to different sources. In the case of ANOVA, these sources are the variation between groups and the variation within groups. ANOVA was developed by the statistician Ronald Fisher. In its simplest form, it provides a statistical test of whether two or more population means are equal, and therefore generalizes the Student's t-test#Independent two-sample t-test, ''t''- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |