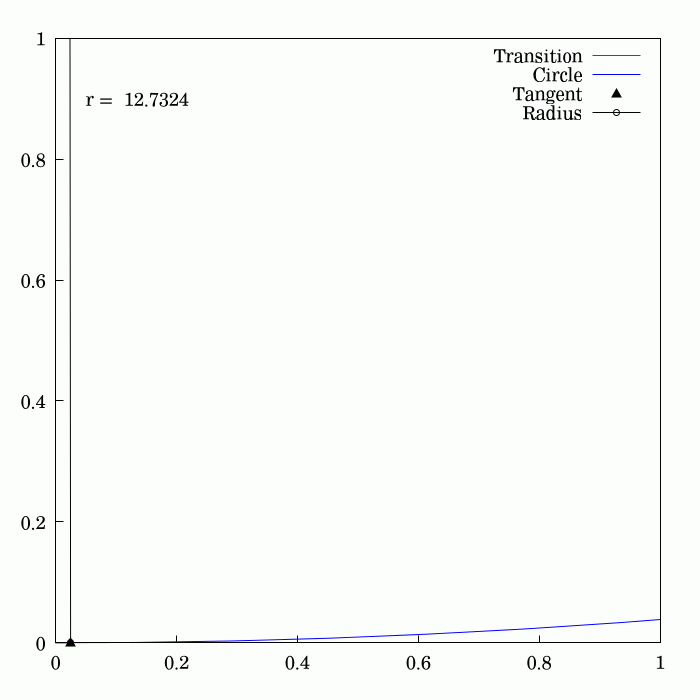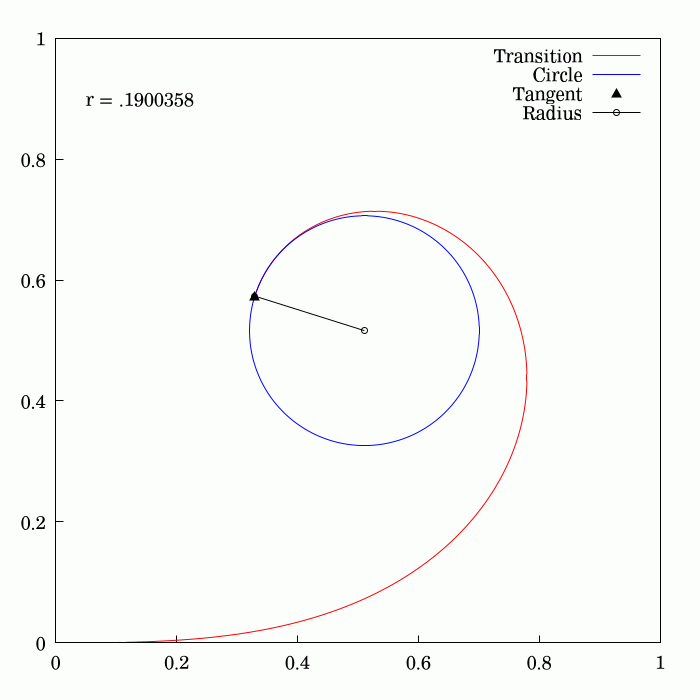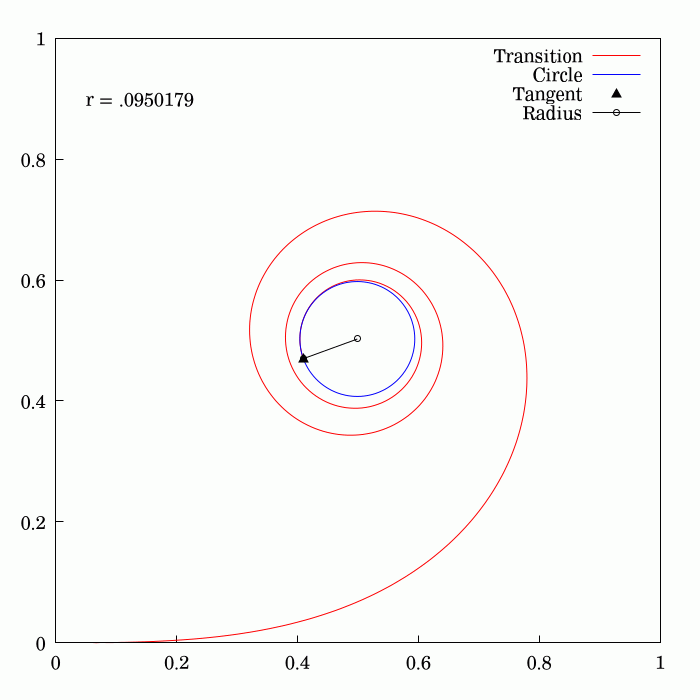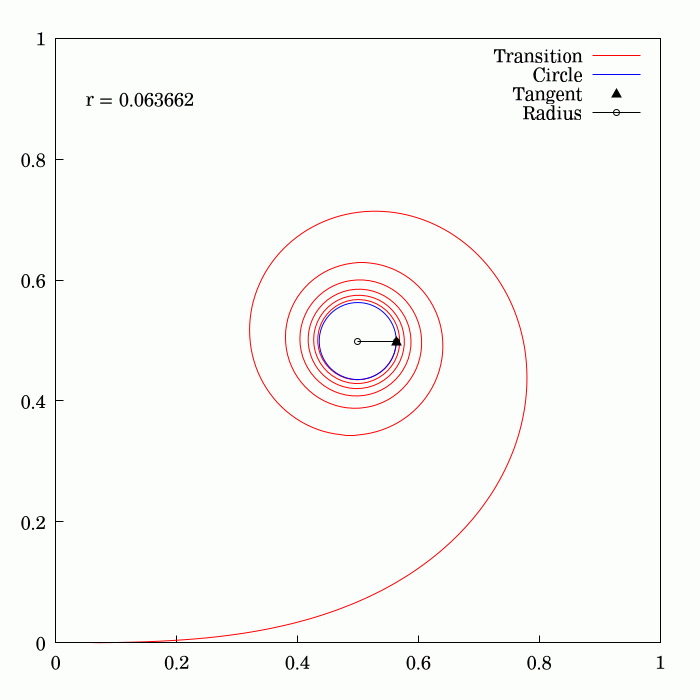
|
Track Transition Curves
A track transition curve, or spiral easement, is a mathematically-calculated curve on a section of highway, or railroad track, in which a straight section changes into a curve. It is designed to prevent sudden changes in lateral (or centripetal) acceleration. In plane (viewed from above), the start of the transition of the horizontal curve is at infinite radius, and at the end of the transition, it has the same radius as the curve itself and so forms a very broad spiral. At the same time, in the vertical plane, the outside of the curve is gradually raised until the correct degree of bank is reached. If such an easement were not applied, the lateral acceleration of a rail vehicle would change abruptly at one point (the tangent point where the straight track meets the curve) with undesirable results. With a road vehicle, a transition curve allows the driver to alter the steering in a gradual manner. History On early railroads, because of the low speeds and wide-radius curves emp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Easement Curve
A track transition curve, or spiral easement, is a mathematically-calculated curve on a section of highway, or railroad track, in which a straight section changes into a curve. It is designed to prevent sudden changes in lateral (or centripetal) acceleration. In plane (viewed from above), the start of the transition of the horizontal curve is at infinite radius, and at the end of the transition, it has the same radius as the curve itself and so forms a very broad spiral. At the same time, in the vertical plane, the outside of the curve is gradually raised until the correct degree of bank is reached. If such an easement were not applied, the lateral acceleration of a rail vehicle would change abruptly at one point (the tangent point where the straight track meets the curve) with undesirable results. With a road vehicle, a transition curve allows the driver to alter the steering in a gradual manner. History On early railroads, because of the low speeds and wide-radius curves emp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur N
Arthur is a common male given name of Brythonic origin. Its popularity derives from it being the name of the legendary hero King Arthur. The etymology is disputed. It may derive from the Celtic ''Artos'' meaning “Bear”. Another theory, more widely believed, is that the name is derived from the Roman clan '' Artorius'' who lived in Roman Britain for centuries. A common spelling variant used in many Slavic, Romance, and Germanic languages is Artur. In Spanish and Italian it is Arturo. Etymology The earliest datable attestation of the name Arthur is in the early 9th century Welsh-Latin text ''Historia Brittonum'', where it refers to a circa 5th to 6th-century Briton general who fought against the invading Saxons, and who later gave rise to the famous King Arthur of medieval legend and literature. A possible earlier mention of the same man is to be found in the epic Welsh poem ''Y Gododdin'' by Aneirin, which some scholars assign to the late 6th century, though this is still a mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Railway Systems Engineering
Railway engineering is a multi-faceted engineering discipline dealing with the design, construction and operation of all types of rail transport systems. It encompasses a wide range of engineering disciplines, including civil engineering, computer engineering, electrical engineering, mechanical engineering, industrial engineering and production engineering. A great many other engineering sub-disciplines are also called upon. History With the advent of the railways in the early nineteenth century, a need arose for a specialized group of engineers capable of dealing with the unique problems associated with railway engineering. As the railways expanded and became a major economic force, a great many engineers became involved in the field, probably the most notable in Britain being Richard Trevithick, George Stephenson and Isambard Kingdom Brunel. Today, railway systems engineering continues to be a vibrant field of engineering. Subfields *Mechanical engineering * Command, cont ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum Railway Curve Radius
The minimum railway curve radius is the shortest allowable design radius for the centerline of railway tracks under a particular set of conditions. It has an important bearing on construction costs and operating costs and, in combination with superelevation (difference in elevation of the two rails) in the case of train tracks, determines the maximum safe speed of a curve. The minimum radius of a curve is one parameter in the design of railway vehicles as well as trams; monorails and automated guideways are also subject to a minimum radius. History The first proper railway was the Liverpool and Manchester Railway, which opened in 1830. Like the tram roads that had preceded it over a hundred years, the L&M had gentle curves and gradients. Reasons for these gentle curves include the lack of strength of the track, which might have overturned if the curves were too sharp causing derailments. The gentler the curves, the greater the visibility, thus boosting safety via increased ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Of Curvature
Degree of curve or degree of curvature is a measure of curvature of a circular arc used in civil engineering for its easy use in layout surveying. Definition The degree of curvature is defined as the central angle to the ends of an agreed length of either an arc or a chord; various lengths are commonly used in different areas of practice. This angle is also the change in forward direction as that portion of the curve is traveled. In an ''n''-degree curve, the forward bearing changes by ''n'' degrees over the standard length of arc or chord. Usage Curvature is usually measured in radius of curvature. A small circle can be easily laid out by just using radius of curvature, but degree of curvature is more convenient for calculating and laying out the curve if the radius is large as a kilometer or a mile, as it needed for large scale works like roads and railroads. By using degrees of curvature, curve setting can be easily done with the help of a transit or theodolite and a chai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fresnel Integral
250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The simultaneous parametric plot of and is the Euler spiral (also known as the Cornu spiral or clothoid). Definition 250px, Fresnel integrals with arguments instead of converge to instead of . The Fresnel integrals admit the following power series expansions that converge for all : \begin S(x) &= \int_0^x \sin\left(t^2\right)\,dt = \sum_^(-1)^n \frac, \\ C(x) &= \int_0^x \cos\left(t^2\right)\,dt = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in an ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cant (road/rail)
The cant of a railway track or camber of a road (also referred to as superelevation, cross slope or cross fall) is the rate of change in elevation (height) between the two rails or edges. This is normally greater where the railway or road is curved; raising the outer rail or the outer edge of the road creates a banked turn, thus allowing vehicles to maneuver through the curve at higher speeds than would otherwise be possible were the surface flat or level. Rail On railways, cant helps a train steer around a curve, keeping the wheel flanges from touching the rails, minimizing friction, wear and rail squeal. The main functions of cant are the following: * Improve distribution of the load across both rails * Reduce wear on rails and wheels * Neutralize the effect of lateral forces * Improve passenger comfort The necessary cant in a curve depends on the expected speed of the trains and the radius. However, it may be necessary to select a compromise value at design time, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Arc
Circular may refer to: * The shape of a circle * ''Circular'' (album), a 2006 album by Spanish singer Vega * Circular letter (other) ** Flyer (pamphlet), a form of advertisement * Circular reasoning, a type of logical fallacy * Circular reference * Government circular, a written statement of government policy See also * Circular DNA (other) * Circular Line (other) Circle Line or circular line is an expression commonly used to describe a circle route in a public transport network or system. Circle Line or Circular line may also refer to: Railways Asia Bangladesh * Chittagong Circular Railway China ... * Circularity (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as ax^2 + bx + c = 0\,, where represents an unknown (mathematics), unknown value, and , , and represent known numbers, where . (If and then the equation is linear equation, linear, not quadratic.) The numbers , , and are the ''coefficients'' of the equation and may be distinguished by respectively calling them, the ''quadratic coefficient'', the ''linear coefficient'' and the ''constant'' or ''free term''. The values of that satisfy the equation are called ''solution (mathematics), solutions'' of the equation, and ''zero of a function, roots'' or ''zero of a function, zeros'' of the Expression (mathematics), expression on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two complex number, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Railway Engineering And Maintenance-of-Way Association
American(s) may refer to: * American, something of, from, or related to the United States of America, commonly known as the "United States" or "America" ** Americans, citizens and nationals of the United States of America ** American ancestry, people who self-identify their ancestry as "American" ** American English, the set of varieties of the English language native to the United States ** Native Americans in the United States, indigenous peoples of the United States * American, something of, from, or related to the Americas, also known as "America" ** Indigenous peoples of the Americas * American (word), for analysis and history of the meanings in various contexts Organizations * American Airlines, U.S.-based airline headquartered in Fort Worth, Texas * American Athletic Conference, an American college athletic conference * American Recordings (record label), a record label previously known as Def American * American University, in Washington, D.C. Sports teams Soccer * Ba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position (geometry), position of an element (i.e., Point (mathematics), point). This is the informal meaning of the term dimension. In mathematics, a tuple of Real number, numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the -dimensional Euclidean space. When , this space is called three-dimensional Euclidean space (or simply Euclidean space when the context is clear). It serves as a model of the physical universe (when relativity theory is not considered), in which all known matter exists. While this space remains the most compelling and useful way to model the world as it is experienced, it is only one example of a large variety of spaces in three dimensions called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpeg/1200px-Brusio_Viaduct_(158241421).jpeg "Click for more on -> Easement Curve")
