|
Tissot's Indicatrix
In cartography, a Tissot's indicatrix (Tissot indicatrix, Tissot's ellipse, Tissot ellipse, ellipse of distortion) (plural: "Tissot's indicatrices") is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 and 1871 in order to characterize local distortions due to map projection. It is the geometry that results from Projection (linear algebra), projecting a circle of infinitesimal radius from a curved geometric model, such as a globe, onto a map. Tissot proved that the resulting diagram is an ellipse whose axes indicate the two Principal curvature, principal directions along which scale is maximal and minimal at that point on the map. A single indicatrix describes the distortion at a single point. Because distortion varies across a map, generally Tissot's indicatrices are placed across a map to illustrate the spatial change in distortion. A common scheme places them at each intersection of displayed meridians and parallels. These schematics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tissot World From Space
Tissot SA () is a Swiss luxury watch brand owned by the Swatch Group. The company was founded in Le Locle, Switzerland by Charles-Félicien Tissot and his son, Charles-Émile Tissot, in 1853. Tissot is not associated with Mathey-Tissot, another Swiss watchmaking firm. History Independent company Tissot was founded in 1853 by Charles-Félicien Tissot and his son Charles-Émile Tissot in the Swiss city of Le Locle, in the Neuchâtel canton of the Jura Mountains area. The father and son team worked as a casemaker (Charles-Félicien Tissot) and watchmaker (Charles-Emile). His son having expressed an interest in watchmaking from a young age. The two turned their house at the time into a small 'factory'. Charles-Emile Tissot left for Russia in 1858 and succeeded in selling their savonnette pocket watches across the Russian Empire. Russia became Tissot's greatest market, with the brand gaining popularity even in the Tsar's court; so Charles Tissot, Charles-Émile's son, moved to Mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meridian (geography)
In geography and geodesy, a meridian is the locus connecting points of equal longitude, which is the angle (in degrees or other units) east or west of a given prime meridian (currently, the IERS Reference Meridian). In other words, it is a coordinate line for longitudes, a line of longitude. The position of a point along the meridian at a given longitude is given by its latitude, measured in angular degrees north or south of the Equator. On a Mercator projection or on a Gall-Peters projection, each meridian is perpendicular to all circles of latitude. Assuming a spherical Earth, a meridian is a great semicircle on Earth's surface. Adopting instead a spheroidal or ellipsoid model of Earth, the meridian is half of a north-south great ellipse. The length of a meridian is twice the length of an Earth quadrant, equal to on a modern ellipsoid ( WGS 84). Pre-Greenwich The first prime meridian was set by Eratosthenes in 200 BC. This prime meridian was used to provide mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robinson Projection
The Robinson projection is a map projection of a world map that shows the entire world at once. It was specifically created in an attempt to find a good compromise to the problem of readily showing the whole globe as a flat image. The Robinson projection was devised by Arthur H. Robinson in 1963 in response to an appeal from the Rand McNally company, which has used the projection in general-purpose world maps since that time. Robinson published details of the projection's construction in 1974. The National Geographic Society (NGS) began using the Robinson projection for general-purpose world maps in 1988, replacing the Van der Grinten projection. In 1998, the NGS abandoned the Robinson projection for that use in favor of the Winkel tripel projection, as the latter "reduces the distortion of land masses as they near the poles". Strengths and weaknesses The Robinson projection is neither equal-area nor conformal, abandoning both for a compromise. The creator felt that this pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinusoidal Projection
The sinusoidal projection is a pseudocylindrical equal-area map projection, sometimes called the Sanson–Flamsteed or the Mercator equal-area projection. Jean Cossin of Dieppe was one of the first mapmakers to use the sinusoidal, using it in a world map in 1570. The projection represents the poles as points, as they are on the sphere, but the meridians and continents are distorted. The equator and the central meridian are the most accurate parts of the map, having no distortion at all, and the further away from those that one examines, the greater the distortion. The projection is defined by: :\begin x &= \left(\lambda - \lambda_0\right) \cos \varphi \\ y &= \varphi\,\end where \varphi is the latitude, ''λ'' is the longitude, and ''λ'' is the longitude of the central meridian. Scale is constant along the central meridian, and east–west scale is constant throughout the map. Therefore, the length of each parallel on the map is proportional to the cosine of the latitude, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Cylindrical Equal-area Projection
In cartography, the Lambert cylindrical equal-area projection, or Lambert cylindrical projection, is a cylindrical equal-area projection. This projection is undistorted along the equator, which is its standard parallel, but distortion increases rapidly towards the poles. Like any cylindrical projection, it stretches parallels increasingly away from the equator. The poles accrue infinite distortion, becoming lines instead of points. History The projection was invented by the Swiss mathematician Johann Heinrich Lambert and described in his 1772 treatise, ''Beiträge zum Gebrauche der Mathematik und deren Anwendung'', part III, section 6: ''Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten'', translated as, ''Notes and Comments on the Composition of Terrestrial and Celestial Maps''. Lambert's projection is the basis for the cylindrical equal-area projection family. Lambert chose the equator as the parallel of no distortion. By multiplying the projection's heig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transverse Mercator Projection
The transverse Mercator map projection (TM, TMP) is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the Universal Transverse Mercator. When paired with a suitable geodetic datum, the transverse Mercator delivers high accuracy in zones less than a few degrees in east-west extent. Standard and transverse aspects The transverse Mercator projection is the transverse aspect of the standard (or ''Normal'') Mercator projection. They share the same underlying mathematical construction and consequently the transverse Mercator inherits many traits from the normal Mercator: * Both projections are cylindrical: for the normal Mercator, the axis of the cylinder coincides with the polar axis and the line of tangency with the equator. For the transverse Mercator, the axis of the cylinder lies in the equatorial plane, and the line of tangency is any chosen meridian, thereby desi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fuller Projection
The Dymaxion map projection, also called the Fuller projection, is a kind of polyhedral map projection of the Earth's surface onto the unfolded net of an icosahedron. The resulting map is heavily interrupted in order to reduce shape and size distortion compared to other world maps, but the interruptions are chosen to lie in the ocean. The projection was invented by Buckminster Fuller. In 1943, Fuller proposed a projection onto a cuboctahedron, which he called the ''Dymaxion World'', using the name ''Dymaxion'' which he also applied to several of his other inventions. In 1954, Fuller and cartographer Shoji Sadao produced an updated Dymaxion map, the Airocean World Map, based on an icosahedron with a few of the triangular faces cut to avoid breaks in landmasses. The Dymaxion projection is intended for representations of the entire Earth. History The March 1, 1943, edition of ''Life'' magazine included a photographic essay titled "Life Presents R. Buckminster Fuller's Dymaxion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Azimuthal Equidistant Projection
The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionally correct distances from the center point, and that all points on the map are at the correct azimuth (direction) from the center point. A useful application for this type of projection is a polar projection which shows all meridians (lines of longitude) as straight, with distances from the pole represented correctly. The United Nations flag, flag of the United Nations contains an example of a polar azimuthal equidistant projection. History While it may have been used by ancient Egyptians for star maps in some holy books,, p.29 the earliest text describing the azimuthal equidistant projection is an 11th-century work by Abu Rayhan Biruni, al-Biruni. The first use of the projection on a terrestrial map is the pair of hemispheres by Heinrich Glarean, Glareanus of about 1510. Another early example of this system is the world map by ‛Ali b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Winkel Tripel Projection
The Winkel tripel projection (Winkel III), a modified azimuthal map projection of the world map, world, is one of Winkel projection, three projections proposed by German cartographer Oswald Winkel (7 January 1874 – 18 July 1953) in 1921. The projection is the arithmetic mean of the equirectangular projection and the Aitoff projection: The name (German language, German for 'triple') refers to Winkel's goal of minimizing three Map projection#Metric properties of maps, kinds of distortion: area, direction, and distance. Algorithm : \begin x &= \frac \left(\lambda \cos \varphi_1 + \frac\right), \\ y &= \frac \left(\varphi + \frac\right), \end where ''λ'' is the longitude relative to the central meridian of the projection, ''φ'' is the latitude, ''φ'' is the standard parallel for the equirectangular projection, sinc is the sinc function, unnormalized cardinal sine function, and : \alpha = \arccos\left(\cos\varphi \cos \frac \right). In his proposal, Winkel set : \varphi_1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mollweide Projection
400px, Mollweide projection of the world 400px, The Mollweide projection with Tissot's indicatrix of deformation The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions. The projection was first published by mathematician and astronomer Karl (or Carl) Brandan Mollweide (1774–1825) of Leipzig in 1805. It was reinvented and popularized in 1857 by Jacques Babinet, who gave it the name homalographic projection. The variation homolographic arose from frequent nineteenth-century usage in star atlases. Properties The Mollweide is a pseudocylindrical projection in which the equator is represented as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
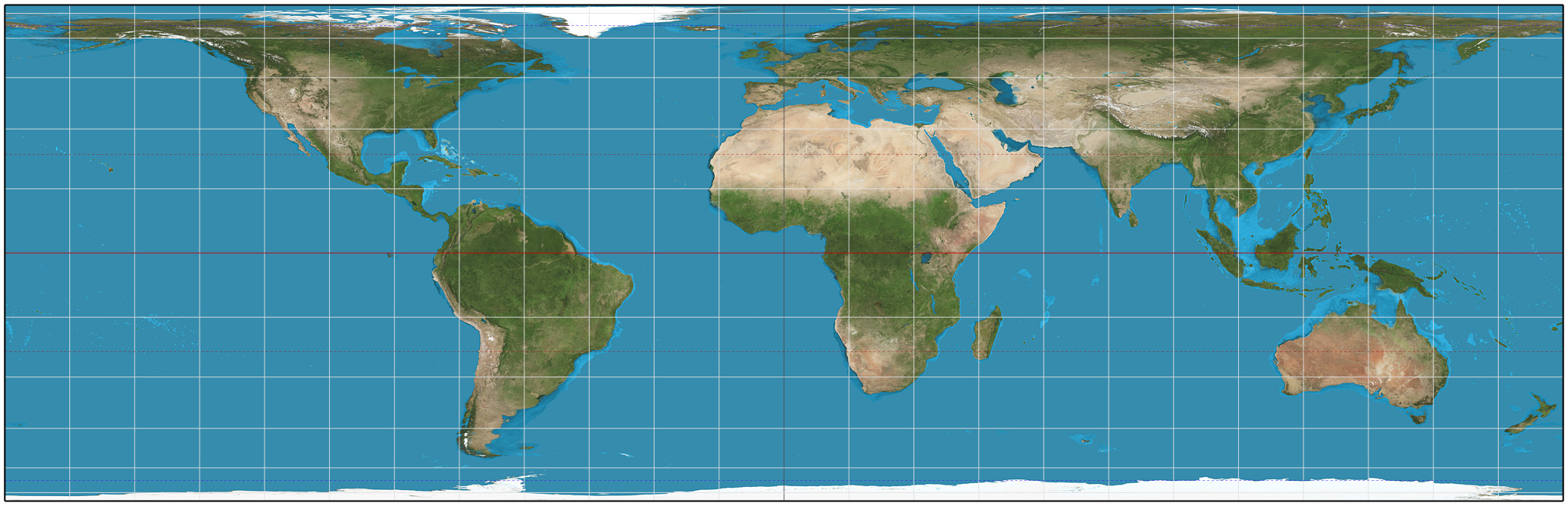
Gall–Peters Projection
The Gall–Peters projection is a rectangular, Equal-area projection, equal-area map projection. Like all equal-area projections, it distorts most shapes. It is a cylindrical equal-area projection with latitudes 45° north and south as the regions on the map that have no distortion. The projection is named after James Gall and Arno Peters. Gall described the projection in 1855 at a science convention and published a paper on it in 1885. Peters brought the projection to a wider audience beginning in the early 1970s through his "Peters World Map". The name "Gall–Peters projection" was first used by Arthur H. Robinson in a pamphlet put out by the American Cartographic Association in 1986.American Cartographic Association's Committee on Map Projections, 1986. ''Which Map is Best'' p. 12. Falls Church: American Congress on Surveying and Mapping. The Gall–Peters projection achieved notoriety in the late 20th century as the centerpiece of a controversy about the political implication ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |