|
Term Discrimination
Term discrimination is a way to rank keywords in how useful they are for information retrieval. Overview This is a method similar to tf-idf but it deals with finding keywords suitable for information retrieval and ones that are not. Please refer to Vector Space Model first. This method uses the concept of ''Vector Space Density'' that the less dense an occurrence matrix is, the better an information retrieval query will be. An optimal index term is one that can distinguish two different documents from each other and relate two similar documents. On the other hand, a sub-optimal index term can not distinguish two different document from two similar documents. The discrimination value is the difference in the occurrence matrix's vector-space density versus the same matrix's vector-space without the index term's density. Let: A be the occurrence matrix A_k be the occurrence matrix without the index term k and Q(A) be density of A. Then: The discrimination value of the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Retrieval
Information retrieval (IR) in computing and information science is the task of identifying and retrieving information system resources that are relevant to an Information needs, information need. The information need can be specified in the form of a search query. In the case of document retrieval, queries can be based on full-text search, full-text or other content-based indexing. Information retrieval is the science of searching for information in a document, searching for documents themselves, and also searching for the metadata that describes data, and for databases of texts, images or sounds. Automated information retrieval systems are used to reduce what has been called information overload. An IR system is a software system that provides access to books, journals and other documents; it also stores and manages those documents. Web search engines are the most visible IR applications. Overview An information retrieval process begins when a user enters a query into the sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
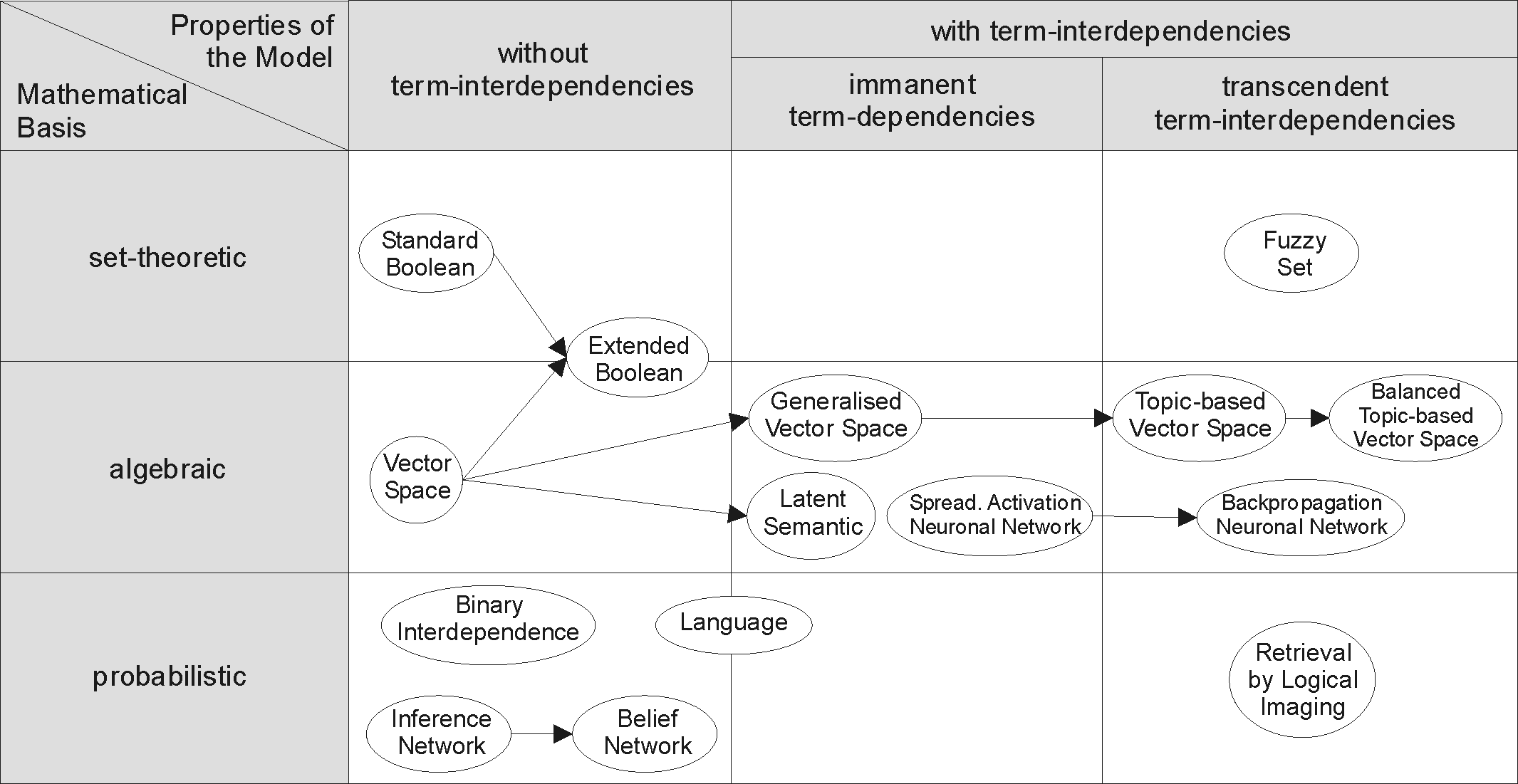
Vector Space Model
Vector space model or term vector model is an algebraic model for representing text documents (or more generally, items) as vector space, vectors such that the distance between vectors represents the relevance between the documents. It is used in information filtering, information retrieval, index (search engine), indexing and relevancy rankings. Its first use was in the SMART Information Retrieval System. Definitions In this section we consider a particular vector space model based on the Bag-of-words model, bag-of-words representation. Documents and queries are represented as vectors. :d_j = ( w_ ,w_ , \dotsc ,w_ ) :q = ( w_ ,w_ , \dotsc ,w_ ) Each Dimension (vector space), dimension corresponds to a separate term. If a term occurs in the document, its value in the vector is non-zero. Several different ways of computing these values, also known as (term) weights, have been developed. One of the best known schemes is tf-idf weighting (see the example below). The definition of ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Occurrence Matrix
A document-term matrix is a mathematical matrix that describes the frequency of terms that occur in each document in a collection. In a document-term matrix, rows correspond to documents in the collection and columns correspond to terms. This matrix is a specific instance of a document-feature matrix where "features" may refer to other properties of a document besides terms. It is also common to encounter the transpose, or term-document matrix where documents are the columns and terms are the rows. They are useful in the field of natural language processing and computational text analysis. While the value of the cells is commonly the raw count of a given term, there are various schemes for weighting the raw counts such as row normalizing (i.e. relative frequency/proportions) and tf-idf. Terms are commonly single words separated by whitespace or punctuation on either side (a.k.a. unigrams). In such a case, this is also referred to as "bag of words" representation because the count ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the figure. The same definition extends to any object in n-dimensional Euclidean space. In geometry, one often assumes uniform mass density, in which case the '' barycenter'' or ''center of mass'' coincides with the centroid. Informally, it can be understood as the point at which a cutout of the shape (with uniformly distributed mass) could be perfectly balanced on the tip of a pin. In physics, if variations in gravity are considered, then a '' center of gravity'' can be defined as the weighted mean of all points weighted by their specific weight. In geography, the centroid of a radial projection of a region of the Earth's surface to sea level is the region's geographical center. History The term "centroid" was coined in 1814. It is used as a substitute for the older terms "center of grav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras. In the Greek deductive geometry exemplified by Euclid's ''Elements'', distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass tool used to draw a circle, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., ''m'' × ''n'' for an ''m'' × ''n'' matrix) is sometimes referred to as the sparsity of the matrix. Conceptually, sparsity corresponds to systems with few pairwise interactions. For example, consider a line of balls connected by springs from one to the next: this is a sparse system, as only adjacent balls are coupled. By contrast, if the same line of balls were to have springs connecting each ball to all other balls, the system would correspond to a dense matrix. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Precision And Recall
In pattern recognition, information retrieval, object detection and classification (machine learning), precision and recall are performance metrics that apply to data retrieved from a collection, corpus or sample space. Precision (also called positive predictive value) is the fraction of relevant instances among the retrieved instances. Written as a formula: \text = \frac Recall (also known as sensitivity) is the fraction of relevant instances that were retrieved. Written as a formula: \text = \frac Both precision and recall are therefore based on relevance. Consider a computer program for recognizing dogs (the relevant element) in a digital photograph. Upon processing a picture which contains ten cats and twelve dogs, the program identifies eight dogs. Of the eight elements identified as dogs, only five actually are dogs ( true positives), while the other three are cats ( false positives). Seven dogs were missed ( false negatives), and seven cats were correctly ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gerard Salton
Gerard A. "Gerry" Salton (8 March 1927 – 28 August 1995) was a professor of computer science at Cornell University. Salton was perhaps the leading computer scientist working in the field of information retrieval during his time, and "the father of Information Retrieval". His group at Cornell developed the SMART Information Retrieval System, which he initiated when he was at Harvard. It was the first system to use the now popular vector space model for information retrieval. Education and career Salton was born Gerhard Anton Sahlmann in Nuremberg, Germany. He came to the United States in 1947 and was naturalized in 1952. He received a Bachelor's (1950) and Master's (1952) degree in mathematics from Brooklyn College, and a Ph.D. from Harvard in applied mathematics in 1958, the last of Howard Aiken's doctoral students, and taught there until 1965, when he joined Cornell University and co-founded its department of Computer Science. Salton was perhaps most well known for develop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |