|
Steiner Circumellipse
In geometry, the Steiner ellipse of a triangle, also called the Steiner circumellipse to distinguish it from the Steiner inellipse, is the unique circumellipse (ellipse that touches the triangle at its vertex (geometry), vertices) whose center is the triangle's centroid.Weisstein, Eric W. "Steiner Circumellipse." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/SteinerCircumellipse.html Named after Jakob Steiner, it is an example of a circumconic. By comparison the circumcircle of a triangle is another circumconic that touches the triangle at its vertices, but is not centered at the triangle's centroid unless the triangle is equilateral triangle, equilateral. The area of the Steiner ellipse equals the area of the triangle times \frac, and hence is 4 times the area of the Steiner inellipse. The Steiner ellipse has the least area of any ellipse circumscribed about the triangle. The Steiner ellipse is the scaled Steiner inellipse (factor 2, center is the centro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steiner Ellipse
In geometry, the Steiner ellipse of a triangle, also called the Steiner circumellipse to distinguish it from the Steiner inellipse, is the unique circumellipse (ellipse that touches the triangle at its vertices) whose center is the triangle's centroid.Weisstein, Eric W. "Steiner Circumellipse." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/SteinerCircumellipse.html Named after Jakob Steiner, it is an example of a circumconic. By comparison the circumcircle of a triangle is another circumconic that touches the triangle at its vertices, but is not centered at the triangle's centroid unless the triangle is equilateral. The area of the Steiner ellipse equals the area of the triangle times \frac, and hence is 4 times the area of the Steiner inellipse. The Steiner ellipse has the least area of any ellipse circumscribed about the triangle. The Steiner ellipse is the scaled Steiner inellipse (factor 2, center is the centroid). Hence both ellipses are similar (h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Conic
In triangle geometry, a triangle conic is a conic in the plane of the reference triangle and associated with it in some way. For example, the circumcircle and the incircle of the reference triangle are triangle conics. Other examples are the Steiner ellipse which is an ellipse passing through the vertices and having its centre at the centroid of the reference triangle, the Kiepert hyperbola which is a conic passing through the vertices, the centroid and the orthocentre of the reference triangle and the Artzt parabolas which are parabolas touching two sidelines of the reference triangle at vertices of the triangle. The terminology of ''triangle conic'' is widely used in the literature without a formal definition,that is, without precisely formulating the relations a conic should have with the reference triangle so as to qualify it to be called a triangle conic (see,). WolframMathWorld has a page titled "Triangle conics" which gives a list of 42 items (not all of them are conics) wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trilinear Coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio is the ratio of the perpendicular distances from the point to the sides (extended if necessary) opposite vertices and respectively; the ratio is the ratio of the perpendicular distances from the point to the sidelines opposite vertices and respectively; and likewise for and vertices and . In the diagram at right, the trilinear coordinates of the indicated interior point are the actual distances (, , ), or equivalently in ratio form, for any positive constant . If a point is on a sideline of the reference triangle, its corresponding trilinear coordinate is 0. If an exterior point is on the opposite side of a sideline from the interior of the triangle, its trilinear coordinate associated with that sideline is negative. It is impossible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rytz's Construction
The Rytz’s axis construction is a basic method of descriptive geometry to find the axes, the semi-major axis and semi-minor axis and the vertices of an ellipse, starting from two conjugated half-diameters. If the center and the semi axis of an ellipse are determined the ellipse can be drawn using an ellipsograph or by hand (see ellipse). Rytz’s construction is a classical construction of Euclidean geometry, in which only compass and ruler A ruler, sometimes called a rule, line gauge, or scale, is a device used in geometry and technical drawing, as well as the engineering and construction industries, to measure distances or draw straight lines. Variants Rulers have long ... are allowed as aids. The design is named after its inventor David Rytz of Brugg (1801–1868). Conjugate diameters appear always if a circle or an ellipse is projected parallelly (the rays are parallel) as images of orthogonal diameters of a circle (see second diagram) or as images of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Points
In differential geometry, conjugate points or focal points are, roughly, points that can almost be joined by a 1-parameter family of geodesics. For example, on a sphere, the north-pole and south-pole are connected by any meridian. Another viewpoint is that conjugate points tell when the geodesics fail to be length-minimizing. All geodesics are ''locally'' length-minimizing, but not globally. For example on a sphere, any geodesic passing through the north-pole can be extended to reach the south-pole, and hence any geodesic segment connecting the poles is not (uniquely) ''globally'' length minimizing. This tells us that any pair of antipodal points on the standard 2-sphere are conjugate points.Cheeger, Ebin. ''Comparison Theorems in Riemannian Geometry''. North-Holland Publishing Company, 1975, pp. 17-18. Definition Suppose ''p'' and ''q'' are points on a Riemannian manifold, and \gamma is a geodesic that connects ''p'' and ''q''. Then ''p'' and ''q'' are conjugate points along \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Map
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles. More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. If is the point set of an affine space, then every affine transformation on can be rep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
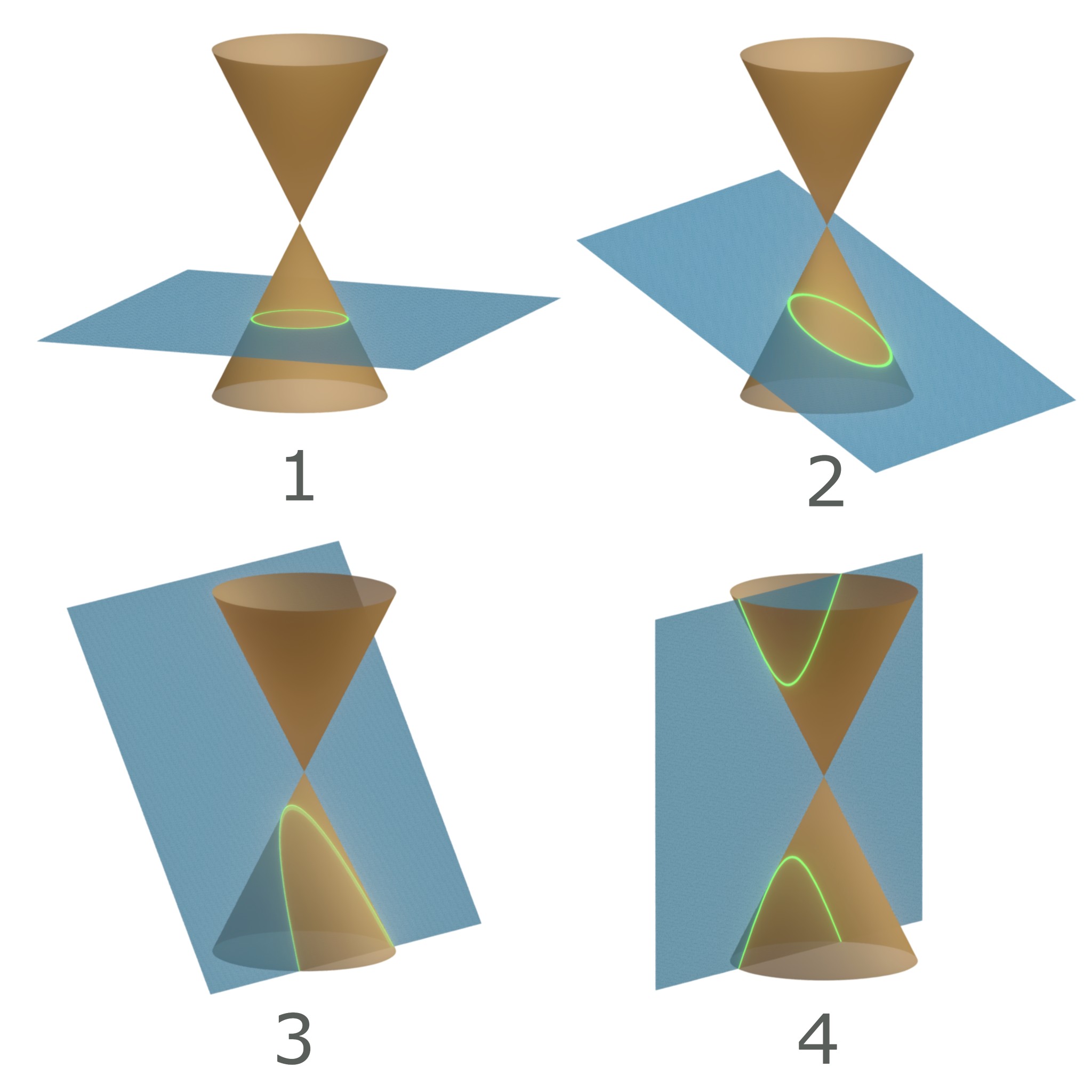
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eccentricity (mathematics)
In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape. More formally two conic sections are similar if and only if they have the same eccentricity. One can think of the eccentricity as a measure of how much a conic section deviates from being circular. In particular: * The eccentricity of a circle is zero. * The eccentricity of an ellipse which is not a circle is greater than zero but less than 1. * The eccentricity of a parabola is 1. * The eccentricity of a hyperbola is greater than 1. * The eccentricity of a pair of lines is \infty Definitions Any conic section can be defined as the locus of points whose distances to a point (the focus) and a line (the directrix) are in a constant ratio. That ratio is called the eccentricity, commonly denoted as . The eccentricity can also be defined in terms of the intersection of a plane and a double-napped cone associated with the conic section. If the cone is orient ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |