|
Squaring The Circle
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square with the area of a circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied the existence of such a square. In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (\pi) is a transcendental number. That is, \pi is not the root of any polynomial with rational coefficients. It had been known for decades that the construction would be impossible if \pi were transcendental, but that fact was not proven until 1882. Approximate constructions with any given non-perfect accuracy exist, and many such constructions have been found. Despite the proof that it is impossible, attempts to square the circle have been common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squaring The Circle
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square with the area of a circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied the existence of such a square. In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (\pi) is a transcendental number. That is, \pi is not the root of any polynomial with rational coefficients. It had been known for decades that the construction would be impossible if \pi were transcendental, but that fact was not proven until 1882. Approximate constructions with any given non-perfect accuracy exist, and many such constructions have been found. Despite the proof that it is impossible, attempts to square the circle have been common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximations Of π
Approximations for the mathematical constant pi () in the history of mathematics reached an accuracy within 0.04% of the true value before the beginning of the Common Era. In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century. Further progress was not made until the 15th century (through the efforts of Jamshīd al-Kāshī). Early modern mathematicians reached an accuracy of 35 digits by the beginning of the 17th century (Ludolph van Ceulen), and 126 digits by the 19th century (Jurij Vega), surpassing the accuracy required for any conceivable application outside of pure mathematics. The record of manual approximation of is held by William Shanks, who calculated 527 digits correctly in 1853. Since the middle of the 20th century, the approximation of has been the task of electronic digital computers (for a comprehensive account, see Chronology of computation of ). On June 8, 2022, the current r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed ''polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two together, may be called a polygon. The segments of a polygonal circuit are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' (singular: vertex) or ''corners''. The interior of a solid polygon is sometimes called its ''body''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. Mathematicians are often concerned only with the bounding polygonal chains of simple polygons and they often define a polygon accordingly. A polygonal boundary may be allowed to cross over itself, creating star polygons and other self-intersecting polygons. A polygon is a 2-dimensional example of the more general polytope in any number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Milü
Milü (; "close ratio"), also known as Zulü ( Zu's ratio), is the name given to an approximation to (pi) found by Chinese mathematician and astronomer Zu Chongzhi in the 5th century. Using Liu Hui's algorithm (which is based on the areas of regular polygons approximating a circle), Zu famously computed to be between 3.1415926 and 3.1415927 and gave two rational approximations of , and , naming them respectively Yuelü (; "approximate ratio") and Milü. is the best rational approximation of with a denominator of four digits or fewer, being accurate to six decimal places. It is within % of the value of , or in terms of common fractions overestimates by less than . The next rational number (ordered by size of denominator) that is a better rational approximation of is , still only correct to six decimal places and hardly closer to than . To be accurate to seven decimal places, one needs to go as far as . For eight, is needed. The accuracy of Milü to the true value of ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zu Chongzhi
Zu Chongzhi (; 429–500 AD), courtesy name Wenyuan (), was a Chinese astronomer, mathematician, politician, inventor, and writer during the Liu Song and Southern Qi dynasties. He was most notable for calculating pi as between 3.1415926 and 3.1415927, a record in accuracy which would not be surpassed for over 800 years. Life and works Chongzhi's ancestry was from modern Baoding, Hebei. To flee from the ravages of war, Zu's grandfather Zu Chang moved to the Yangtze, as part of the massive population movement during the Eastern Jin. Zu Chang () at one point held the position of Chief Minister for the Palace Buildings () within the Liu Song and was in charge of government construction projects. Zu's father, Zu Shuozhi (), also served the court and was greatly respected for his erudition. Zu was born in Jiankang. His family had historically been involved in astronomical research, and from childhood Zu was exposed to both astronomy and mathematics. When he was only a youth his tal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
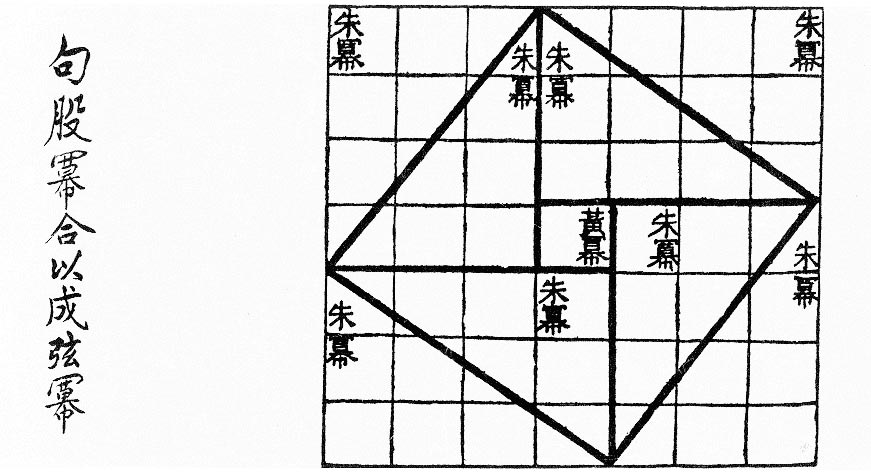
Liu Hui
Liu Hui () was a Chinese mathematician who published a commentary in 263 CE on ''Jiu Zhang Suan Shu (The Nine Chapters on the Mathematical Art).'' He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state of Cao Wei during the Three Kingdoms period (220-280 CE) of China. His major contributions as recorded in his commentary on ''The Nine Chapters on the Mathematical Art'' include a proof of the Pythagorean theorem, theorems in solid geometry, an improvement on Archimedes's approximation of , and a systematic method of solving linear equations in several unknowns. In his other work, ''Haidao Suanjing (The Sea Island Mathematical Manual)'', he wrote about geometrical problems and their application to surveying. He probably visited Luoyang, where he measured the sun's shadow. Mathematical work Liu Hui expressed mathematical results in the form of decimal fractions that utilized metrological units (i.e., related units of length with base 10 s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chinese Mathematics
Mathematics in China emerged independently by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system ( base 2 and base 10), algebra, geometry, number theory and trigonometry. Since the Han Dynasty, as diophantine approximation being a prominent numerical method, the Chinese made substantial progress on polynomial evaluation. Algorithms like regula falsi and expressions like continued fractions are widely used and have been well-documented ever-since. They deliberately find the principal ''n''th root of positive numbers and the roots of equations. The major texts from the period, ''The Nine Chapters on the Mathematical Art'' and the ''Book on Numbers and Computation'' gave detailed processes for solving various mathematical problems in daily life. All procedures were computed using a counting board in both texts, and they included inverse elements as well as Euclidean divi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time,* * * * * * * * * * Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Heath, Thomas L. 1897. ''Works of Archimedes''. Archimedes' other mathematical achievements include deriving an approximation of pi, defining and in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
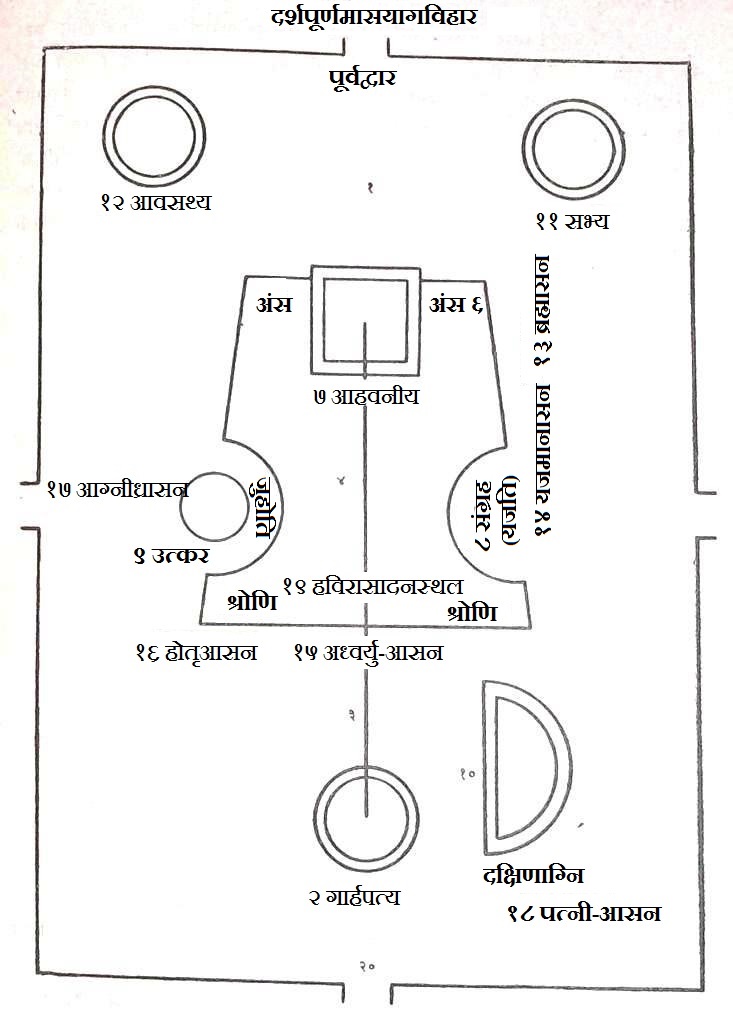
Shulba Sutras
The ''Shulva Sutras'' or ''Śulbasūtras'' (Sanskrit: शुल्बसूत्र; ': "string, cord, rope") are sutra texts belonging to the Śrauta ritual and containing geometry related to fire-altar construction. Purpose and origins The Shulba Sutras are part of the larger corpus of texts called the Shrauta Sutras, considered to be appendices to the Vedas. They are the only sources of knowledge of Indian mathematics from the Vedic period. Unique fire-altar shapes were associated with unique gifts from the Gods. For instance, "he who desires heaven is to construct a fire-altar in the form of a falcon"; "a fire-altar in the form of a tortoise is to be constructed by one desiring to win the world of Brahman" and "those who wish to destroy existing and future enemies should construct a fire-altar in the form of a rhombus"., p. 387, "Certain shapes and sizes of fire-altars were associated with particular gifts that the sacrificer desired from the gods: 'he who desires heaven is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shatapatha Brahmana
The Shatapatha Brahmana ( sa, शतपथब्राह्मणम् , Śatapatha Brāhmaṇam, meaning 'Brāhmaṇa of one hundred paths', abbreviated to 'SB') is a commentary on the Śukla (white) Yajurveda. It is attributed to the Vedic sage Yajnavalkya. Described as the most complete, systematic, and important of the Brahmanas (commentaries on the Vedas), it contains detailed explanations of Vedic sacrificial rituals, symbolism, and mythology. Particularly in its description of sacrificial rituals (including construction of complex fire-altars), the Shatapatha Brahmana (SB) provides scientific knowledge of geometry (e.g. calculations of pi and the root of the Pythagorean theorem) and observational astronomy (e.g. planetary distances and the assertion that the Earth is circular) from the Vedic period. The Shatapatha Brahmana is also considered to be significant in the development of Vaishnavism as the origin of several Puranic legends and avatars of the RigVedic god Vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indian Mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta, Bhaskara II, and Varāhamihira. The decimal number system in use today: "The measure of the genius of Indian civilisation, to which we owe our modern (number) system, is all the greater in that it was the only one in all history to have achieved this triumph. Some cultures succeeded, earlier than the Indian, in discovering one or at best two of the characteristics of this intellectual feat. But none of them managed to bring together into a complete and coherent system the necessary and sufficient conditions for a number-system with the same potential as our own." was first recorded in Indian mathematics. Indian mathematicians made early contributions to the study of the concept of zero as a number,: "...our decimal system, which (by t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Books Of Kings
The Book of Kings (, '' Sēfer Məlāḵīm'') is a book in the Hebrew Bible, found as two books (1–2 Kings) in the Old Testament of the Christian Bible. It concludes the Deuteronomistic history, a history of Israel also including the books of Joshua, Judges and Samuel. Biblical commentators believe the Books of Kings were written to provide a theological explanation for the destruction of the Kingdom of Judah by Babylon in c. 586 BCE and to provide a foundation for a return from Babylonian exile.Sweeney, p1/ref> The two books of Kings present a history of ancient Israel and Judah, from the death of King David to the release of Jehoiachin from imprisonment in Babylon—a period of some 400 years (). Scholars tend to treat the books as consisting of a first edition from the late 7th century BCE and of a second and final edition from the mid-6th century BCE.Fretheim, p. 7 Contents The Jerusalem Bible divides the two Books of Kings into eight sections: *1 Kings 1:1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
_by_Thomas_Degeorge.png "Click for more on -> Archimedes")
