|
Square Of Opposition
In term logic (a branch of philosophical logic), the square of opposition is a diagram representing the relations between the four basic categorical propositions. The origin of the square can be traced back to Aristotle's tractate ''On Interpretation'' and its distinction between two oppositions: contradiction and contrariety. However, Aristotle did not draw any diagram. This was done several centuries later by Apuleius and Boethius. Summary In traditional logic, a proposition (Latin: ''propositio'') is a spoken assertion (''oratio enunciativa''), not the meaning of an assertion, as in modern philosophy of language and logic. A '' categorical proposition'' is a simple proposition containing two terms, subject () and predicate (), in which the predicate is either asserted or denied of the subject. Every categorical proposition can be reduced to one of four logical forms, named , , , and based on the Latin ' (I affirm), for the affirmative propositions and , and ' (I deny), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Of Opposition, Set Diagrams
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ''ABCD'' would be denoted . Characterizations A convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals) * A convex quadrilateral with successiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Terence Parsons
Terence Dwight Parsons (1939-2022) was an American philosopher, specializing in philosophy of language and metaphysics. He was emeritus professor of philosophy at UCLA. Life and career Parsons was born in Endicott, New York and graduated from the University of Rochester with a BA in physics. He received his PhD from Stanford University in 1966. He was a full-time faculty member at the University of Illinois at Chicago from 1965 to 1972, at the University of Massachusetts at Amherst from 1972 to 1979, at the University of California at Irvine from 1979 to 2000, and at the University of California at Los Angeles from 2000 to 2012. In 2007, he was elected to the American Academy of Arts and Sciences. Philosophical work Parsons worked on the semantics of natural language to develop theories of truth and meaning for natural language similar to those devised for artificial languages by philosophical logicians. Heavily influenced by Alexius Meinong, he wrote ''Nonexistent Objects'' (19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Hexagon
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises in a topic-neutral way. When used as a countable noun, the term "a logic" refers to a logical formal system that articulates a proof system. Formal logic contrasts with informal logic, which is associated with informal fallacies, critical thinking, and argumentation theory. While there is no general agreement on how formal and informal logic are to be distinguished, one prominent approach associates their difference with whether the studied arguments are expressed in formal or informal languages. Logic plays a central role in multiple fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises together with a conclusion. Premises and conclusions are usually under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Cube
In the system of Aristotelian logic, the logical cube is a diagram representing the different ways in which each of the eight propositions of the system is logically related ('opposed') to each of the others. The system is also useful in the analysis of syllogistic logic, serving to identify the allowed logical conversions from one type to another.Paul Dekker, 2015, "Not Only Barbara", Journal of Logic, Language, and Information 24(2), pp. 95-129. See also *Logical hexagon Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises ... * Square of opposition References Conceptual models Term logic {{logic-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
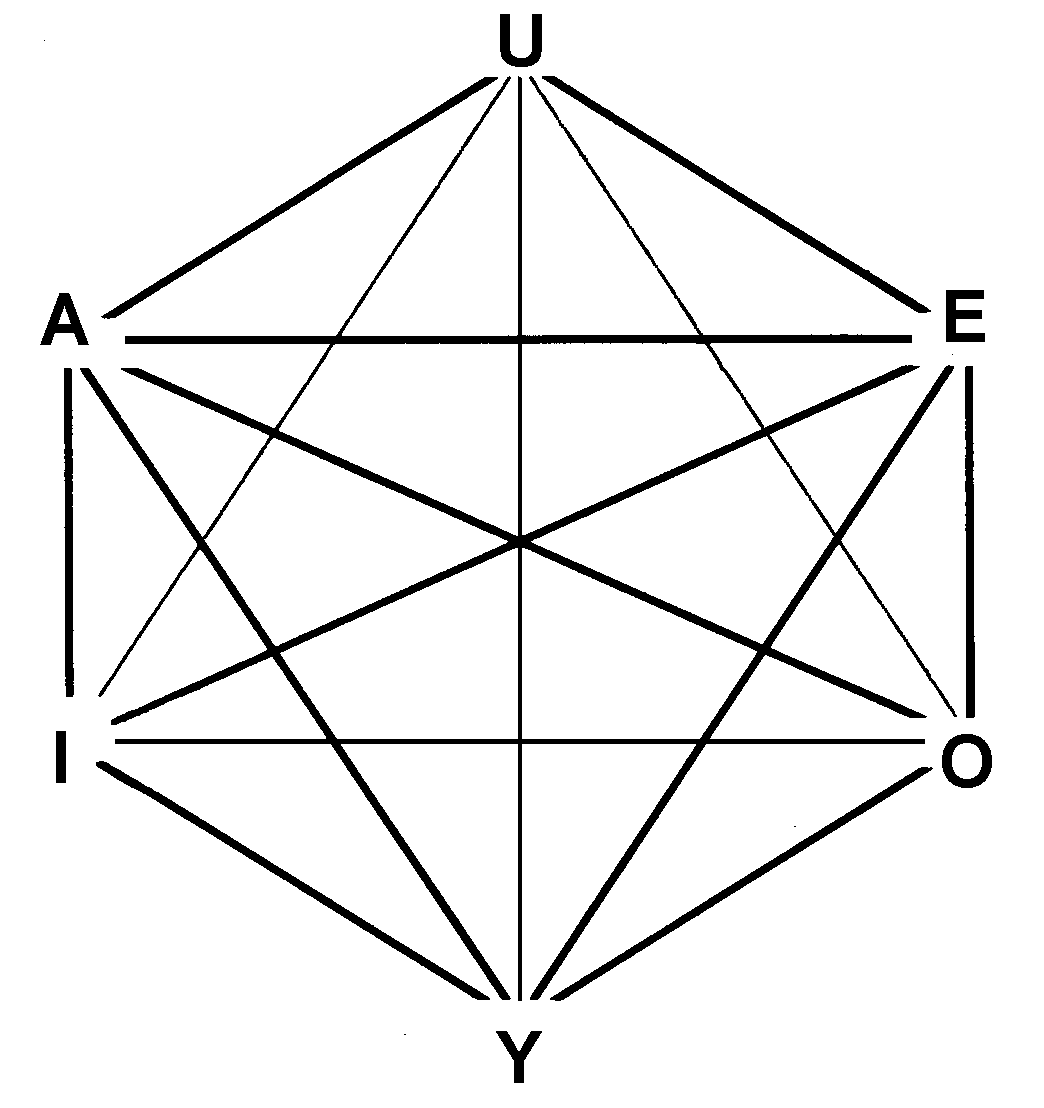Robert Blanché
__NOTOC__ Robert Blanché (1898–1975) was an associate professor of philosophy at the University of Toulouse. He wrote many books addressing the philosophy of mathematics. About ''Structures intellectuelles'' Robert Blanché died in 1975. Nine years before, in 1966, he published with Vrin: ''Structures intellectuelles''. Therein, he deals with the logical hexagon. Whereas the logical square or square of Apuleius represents four values: A,E,I,O , the logical hexagon represents six, that is to say, not only A,E,I,O but also two new values: Y and U. It is advisable to read the article: logical hexagon as well what concerns Indian logic The development of Indian logic dates back to the ''anviksiki'' of Medhatithi Gautama (c. 6th century BCE); the Sanskrit grammar rules of Pāṇini (c. 5th century BCE); the Vaisheshika school's analysis of atomism (c. 6th century BCE to 2nd centur .... In ''La Logique et son histoire d' Aristote à Russell'', published with Armand Colin in 1970, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augustin Sesmat
Augustin Sesmat ( Dieulouard -- ) was a French mathematician and logician. He was professor of history and criticism of science at the Institut Catholique de Paris in the 1930s. He was probably the first person to discover the logical hexagon Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises ..., thus solving a problem posed by Aristotle. Works * ''Le système absolu classique et les mouvements réels'', 1936. * ''Logique. I. Les définitions, les jugements'' . ouvrage publiés avec le concours de CNRS, Paris, 1950, 359 pp. * ''Logique. II. Les raisonnements, la logistique'' . Hermann & Cie, Paris,1951, pp. 361–776. * ''Dialectique, Hamelin et la philosophie chrétienne,'' Bloud & Gay , Paris,1955, 38 pp. References French mathematicians French logicians French philos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiotic Square
The semiotic square, also known as the Greimas square, is a tool used in structural analysis of the relationships between semiotic signs through the opposition of concepts, such as feminine-masculine or beautiful-ugly, and of extending the relevant ontology. The semiotic square, derived from Aristotle's logical square of opposition, was developed by Algirdas J. Greimas, a Lithuanian- French linguist and semiotician, who considered the semiotic square to be the elementary structure of meaning. Greimas first presented the square in ''Semantique Structurale'' (1966), a book which was later published as ''Structural Semantics: An Attempt at a Method'' (1983). He further developed the semiotic square with Francois Rastier in "The Interaction of Semiotic Constraints" (1968). Basic structure The Greimas square is a model based on relationships: *S1 = positive seme *S2 = negative seme *S = complex axis (S1 + S2) *~S = neutral axis (neither S1 nor S2) # The semiotic square is form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algirdas Julien Greimas
Algirdas Julien Greimas (; born ''Algirdas Julius Greimas''; 9 March 1917 – 27 February 1992) was a Lithuanian literary scientist who wrote most of his body of work in French while living in France. Greimas is known among other things for the Greimas Square (''le carré sémiotique''). He is, along with Roland Barthes, considered the most prominent of the French semioticians. With his training in structural linguistics, he added to the theory of signification, plastic semiotics, and laid the foundations for the Parisian school of semiotics. Among Greimas's major contributions to semiotics are the concepts of isotopy, the actantial model, the narrative program, and the semiotics of the natural world. He also researched Lithuanian mythology and Proto-Indo-European religion, and was influential in semiotic literary criticism. Biography Greimas's father, Julius Greimas, 1882–1942, a teacher and later school inspector, was from Liudvinavas in the Suvalkija region of present ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Begriffsschrift
''Begriffsschrift'' (German for, roughly, "concept-script") is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book. ''Begriffsschrift'' is usually translated as ''concept writing'' or ''concept notation''; the full title of the book identifies it as "a formula language, modeled on that of arithmetic, for pure thought." Frege's motivation for developing his formal approach to logic resembled Leibniz's motivation for his ''calculus ratiocinator'' (despite that, in the foreword Frege clearly denies that he achieved this aim, and also that his main aim would be constructing an ideal language like Leibniz's, which Frege declares to be a quite hard and idealistic—though not impossible—task). Frege went on to employ his logical calculus in his research on the foundations of mathematics, carried out over the next quarter century. This is the first work in Analytical Philosophy, a field that future British and Anglo philosophers such as Bertr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gottlob Frege
Friedrich Ludwig Gottlob Frege (; ; 8 November 1848 – 26 July 1925) was a German philosopher, logician, and mathematician. He was a mathematics professor at the University of Jena, and is understood by many to be the father of analytic philosophy, concentrating on the philosophy of language, logic, and mathematics. Though he was largely ignored during his lifetime, Giuseppe Peano (1858–1932), Bertrand Russell (1872–1970), and, to some extent, Ludwig Wittgenstein (1889–1951) introduced his work to later generations of philosophers. Frege is widely considered to be the greatest logician since Aristotle, and one of the most profound philosophers of mathematics ever. His contributions include the development of modern logic in the ''Begriffsschrift'' and work in the foundations of mathematics. His book the ''Foundations of Arithmetic'' is the seminal text of the logicist project, and is cited by Michael Dummett as where to pinpoint the linguistic turn. His philosophical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Venn Diagram
A Venn diagram is a widely used diagram style that shows the logical relation between set (mathematics), sets, popularized by John Venn (1834–1923) in the 1880s. The diagrams are used to teach elementary set theory, and to illustrate simple set relationships in probability, logic, statistics, linguistics and computer science. A Venn diagram uses simple closed curves drawn on a plane to represent sets. Very often, these curves are circles or ellipses. Similar ideas had been proposed before Venn. Christian Weise in 1712 (''Nucleus Logicoe Wiesianoe'') and Leonhard Euler (''Letters to a German Princess'') in 1768, for instance, came up with similar ideas. The idea was popularised by Venn in ''Symbolic Logic'', Chapter V "Diagrammatic Representation", 1881. Details A Venn diagram may also be called a ''set diagram'' or ''logic diagram''. It is a diagram that shows ''all'' possible logical relations between a finite collection of different sets. These diagrams depict element ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Boole
George Boole (; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher, and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in Ireland. He worked in the fields of differential equations and algebraic logic, and is best known as the author of ''The Laws of Thought'' (1854) which contains Boolean algebra. Boolean logic is credited with laying the foundations for the Information Age. Early life Boole was born in 1815 in Lincoln, Lincolnshire, England, the son of John Boole senior (1779–1848), a shoemaker and Mary Ann Joyce. He had a primary school education, and received lessons from his father, but due to a serious decline in business, he had little further formal and academic teaching. William Brooke, a bookseller in Lincoln, may have helped him with Latin, which he may also have learned at the school of Thomas Bainbridge. He was self-taught in modern languages.H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
