|
Silverman–Toeplitz Theorem
In mathematics, the Silverman–Toeplitz theorem, first proved by Otto Toeplitz, is a result in summability theory characterizing matrix summability methods that are regular. A regular matrix summability method is a matrix transformation of a convergent sequence which preserves the limit. by Ruder, Brian, Published 1966, Call number LD2668 .R4 1966 R915, Publisher Kansas State University, Internet Archive An with -valued entries defines a regular summability method |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Otto Toeplitz
Otto Toeplitz (1 August 1881 – 15 February 1940) was a German mathematician working in functional analysis., reprinted in Life and work Toeplitz was born to a Jewish family of mathematicians. Both his father and grandfather were ''Gymnasium'' mathematics teachers and published papers in mathematics. Toeplitz grew up in Breslau and graduated from the ''Gymnasium'' there. He then studied mathematics at the University of Breslau and was awarded a doctorate in algebraic geometry in 1905. In 1906 Toeplitz arrived at Göttingen University, which was then the world's leading mathematical center, and he remained there for seven years. The mathematics faculty included David Hilbert, Felix Klein, and Hermann Minkowski. Toeplitz joined a group of young people working with Hilbert: Max Born, Richard Courant and Ernst Hellinger, with whom he collaborated for many years afterward. At that time Toeplitz began to rework the theory of linear functionals and quadratic forms on ''n''-dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Summability Theory
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit. If a series converges, the individual terms of the series must approach zero. Thus any series in which the individual terms do not approach zero diverges. However, convergence is a stronger condition: not all series whose terms approach zero converge. A counterexample is the harmonic series :1 + \frac + \frac + \frac + \frac + \cdots =\sum_^\infty\frac. The divergence of the harmonic series was proven by the medieval mathematician Nicole Oresme. In specialized mathematical contexts, values can be objectively assigned to certain series whose sequences of partial sums diverge, in order to make meaning of the divergence of the series. A ''summability method'' or ''summation method'' is a partial function from the set of series to values. For example, Cesàro summation assigns Grandi's divergent seri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
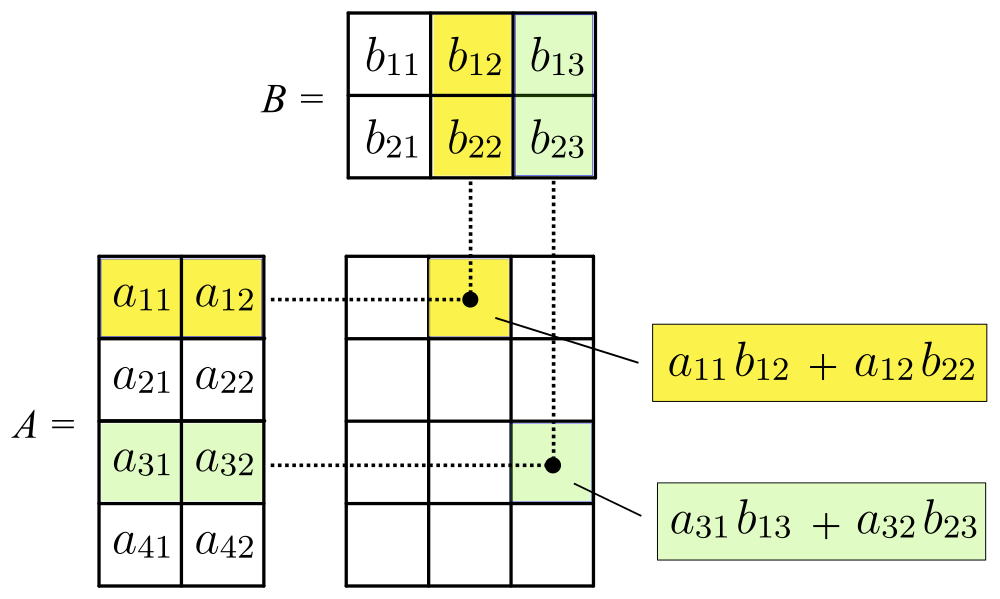
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergent Sequence
As the positive integer n becomes larger and larger, the value n\cdot \sin\left(\tfrac1\right) becomes arbitrarily close to 1. We say that "the limit of the sequence n\cdot \sin\left(\tfrac1\right) equals 1." In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to", and is often denoted using the \lim symbol (e.g., \lim_a_n).Courant (1961), p. 29. If such a limit exists, the sequence is called convergent. A sequence that does not converge is said to be divergent. The limit of a sequence is said to be the fundamental notion on which the whole of mathematical analysis ultimately rests. Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers. History The Greek philosopher Zeno of Elea is famous for formulating paradoxes that involve limiting processes. Leucippus, Democritus, Antiphon, Eudoxus, and Archimedes developed the method of exhaustion, which uses an infinite sequence of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Of A Sequence
As the positive integer n becomes larger and larger, the value n\cdot \sin\left(\tfrac1\right) becomes arbitrarily close to 1. We say that "the limit of the sequence n\cdot \sin\left(\tfrac1\right) equals 1." In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to", and is often denoted using the \lim symbol (e.g., \lim_a_n).Courant (1961), p. 29. If such a limit exists, the sequence is called convergent. A sequence that does not converge is said to be divergent. The limit of a sequence is said to be the fundamental notion on which the whole of mathematical analysis ultimately rests. Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers. History The Greek philosopher Zeno of Elea is famous for formulating paradoxes that involve limiting processes. Leucippus, Democritus, Antiphon, Eudoxus, and Archimedes developed the method of exhaustion, which uses an infinite sequence of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Matrix
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q'', there could be other scenarios where ''P'' is true and ''Q'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cesaro Summation
Cesaro may refer to: * Cesarò, a town in Italy * Cesaro (wrestler) (Claudio Castagnoli, born 1980), a Swiss wrestler * Andrea Cesaro (born 1986), an Italian footballer * Ernesto Cesàro (1859–1906), an Italian mathematician **Cesàro equation **Cesàro summation In mathematical analysis, Cesàro summation (also known as the Cesàro mean ) assigns values to some infinite sums that are not necessarily convergent in the usual sense. The Cesàro sum is defined as the limit, as ''n'' tends to infinity, of ... See also * {{disambiguation, surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
German Language
German ( ) is a West Germanic languages, West Germanic language mainly spoken in Central Europe. It is the most widely spoken and Official language, official or co-official language in Germany, Austria, Switzerland, Liechtenstein, and the Italy, Italian province of South Tyrol. It is also a co-official language of Luxembourg and German-speaking Community of Belgium, Belgium, as well as a national language in Namibia. Outside Germany, it is also spoken by German communities in France (Bas-Rhin), Czech Republic (North Bohemia), Poland (Upper Silesia), Slovakia (Bratislava Region), and Hungary (Sopron). German is most similar to other languages within the West Germanic language branch, including Afrikaans, Dutch language, Dutch, English language, English, the Frisian languages, Low German, Luxembourgish, Scots language, Scots, and Yiddish. It also contains close similarities in vocabulary to some languages in the North Germanic languages, North Germanic group, such as Danish lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Louis Lazarus Silverman
Louis Lazarus Silverman (21 April 1884 – 17 October 1967) was an American mathematician, the first person to receive a Ph.D. in mathematics from an academic institution in the state of Missouri.Zitarelli, Davi"Hilbert in Missouri."Mathematics Magazine 84, no. 5 (2011): 351–364. Born in a village in Lithuania, Silverman moved with his parents to the United States when he was eight years old. He received his B.A. and M.A. in mathematics from Harvard University and then his Ph.D. from the University of Missouri in 1910. From 1910 to 1918 he was a faculty member in the department of mathematics at Cornell University, where he worked with Wallie Abraham Hurwitz on divergent series and summability methods. From 1918 to 1953, Silverman was a professor of mathematics at Dartmouth College Dartmouth College (; ) is a private research university in Hanover, New Hampshire. Established in 1769 by Eleazar Wheelock, it is one of the nine colonial colleges chartered before the American ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |