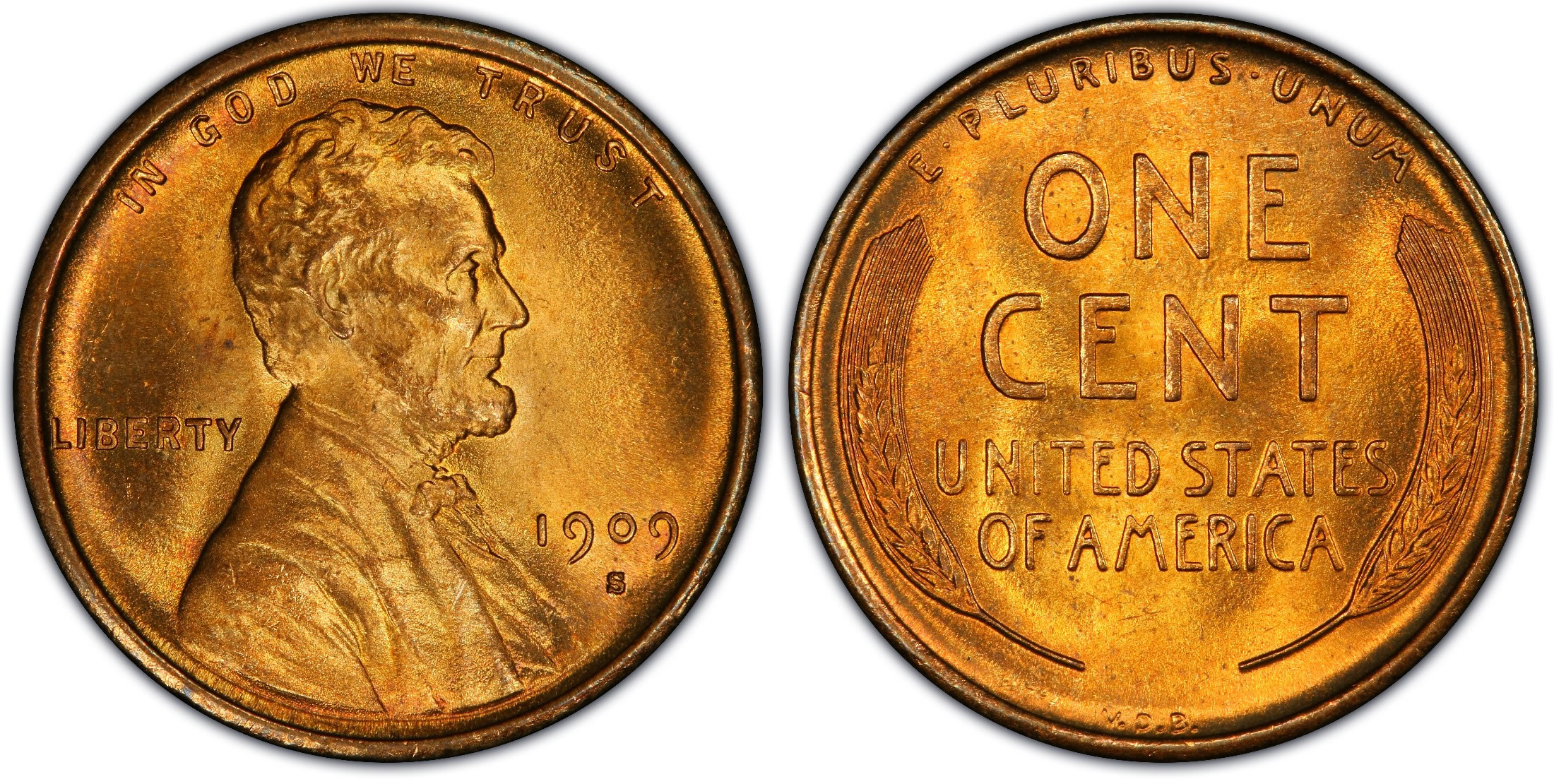|
Sample Maximum And Minimum
In statistics, the sample maximum and sample minimum, also called the largest observation and smallest observation, are the values of the greatest and least elements of a sample. They are basic summary statistics, used in descriptive statistics such as the five-number summary and Bowley's seven-figure summary and the associated box plot. The minimum and the maximum value are the first and last order statistics (often denoted ''X''(1) and ''X''(''n'') respectively, for a sample size of ''n''). If the sample has outliers, they necessarily include the sample maximum or sample minimum, or both, depending on whether they are extremely high or low. However, the sample maximum and minimum need not be outliers, if they are not unusually far from other observations. Robustness The sample maximum and minimum are the ''least'' robust statistics: they are maximally sensitive to outliers. This can either be an advantage or a drawback: if extreme values are real (not measurement errors), a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Absolute Deviation
The average absolute deviation (AAD) of a data set is the average of the absolute deviations from a central point. It is a summary statistic of statistical dispersion or variability. In the general form, the central point can be a mean, median, mode, or the result of any other measure of central tendency or any reference value related to the given data set. AAD includes the mean absolute deviation and the median absolute deviation (both abbreviated as MAD). Measures of dispersion Several measures of statistical dispersion are defined in terms of the absolute deviation. The term "average absolute deviation" does not uniquely identify a measure of statistical dispersion, as there are several measures that can be used to measure absolute deviations, and there are several measures of central tendency that can be used as well. Thus, to uniquely identify the absolute deviation it is necessary to specify both the measure of deviation and the measure of central tendency. Unfort ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
German Tank Problem
In the statistical theory of estimation, the German tank problem consists of estimating the maximum of a discrete uniform distribution from sampling without replacement. In simple terms, suppose there exists an unknown number of items which are sequentially numbered from 1 to ''N''. A random sample of these items is taken and their sequence numbers observed; the problem is to estimate ''N'' from these observed numbers. The problem can be approached using either frequentist inference or Bayesian inference, leading to different results. Estimating the population maximum based on a ''single'' sample yields divergent results, whereas estimation based on ''multiple'' samples is a practical estimation question whose answer is simple (especially in the frequentist setting) but not obvious (especially in the Bayesian setting). The problem is named after its historical application by Allied forces in World War II to the estimation of the monthly rate of German tank production from very ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
UMVU
In statistics a minimum-variance unbiased estimator (MVUE) or uniformly minimum-variance unbiased estimator (UMVUE) is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter. For practical statistics problems, it is important to determine the MVUE if one exists, since less-than-optimal procedures would naturally be avoided, other things being equal. This has led to substantial development of statistical theory related to the problem of optimal estimation. While combining the constraint of unbiasedness with the desirability metric of least variance leads to good results in most practical settings—making MVUE a natural starting point for a broad range of analyses—a targeted specification may perform better for a given problem; thus, MVUE is not always the best stopping point. Definition Consider estimation of g(\theta) based on data X_1, X_2, \ldots, X_n i.i.d. from some member of a family of densities p_\theta, \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Statistic
In statistics, completeness is a property of a statistic in relation to a model for a set of observed data. In essence, it ensures that the distributions corresponding to different values of the parameters are distinct. It is closely related to the idea of identifiability, but in statistical theory it is often found as a condition imposed on a sufficient statistic from which certain optimality results are derived. Definition Consider a random variable ''X'' whose probability distribution belongs to a parametric model ''P''''θ'' parametrized by ''θ''. Say ''T'' is a statistic; that is, the composition of a measurable function with a random sample ''X''1,...,''X''n. The statistic ''T'' is said to be complete for the distribution of ''X'' if, for every measurable function ''g,'': \text\operatorname_\theta(g(T))=0\text\theta\text\mathbf_\theta(g(T)=0)=1\text\theta. The statistic ''T'' is said to be boundedly complete for the distribution of ''X'' if this implication ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sufficient Statistic
In statistics, a statistic is ''sufficient'' with respect to a statistical model and its associated unknown parameter if "no other statistic that can be calculated from the same sample provides any additional information as to the value of the parameter". In particular, a statistic is sufficient for a family of probability distributions if the sample from which it is calculated gives no additional information than the statistic, as to which of those probability distributions is the sampling distribution. A related concept is that of linear sufficiency, which is weaker than ''sufficiency'' but can be applied in some cases where there is no sufficient statistic, although it is restricted to linear estimators. The Kolmogorov structure function deals with individual finite data; the related notion there is the algorithmic sufficient statistic. The concept is due to Sir Ronald Fisher in 1920. Stephen Stigler noted in 1973 that the concept of sufficiency had fallen out of favor in des ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Distribution (discrete)
In probability theory and statistics, the discrete uniform distribution is a symmetric probability distribution wherein a finite number of values are equally likely to be observed; every one of ''n'' values has equal probability 1/''n''. Another way of saying "discrete uniform distribution" would be "a known, finite number of outcomes equally likely to happen". A simple example of the discrete uniform distribution is throwing a fair dice. The possible values are 1, 2, 3, 4, 5, 6, and each time the die is thrown the probability of a given score is 1/6. If two dice are thrown and their values added, the resulting distribution is no longer uniform because not all sums have equal probability. Although it is convenient to describe discrete uniform distributions over integers, such as this, one can also consider discrete uniform distributions over any finite set. For instance, a random permutation is a permutation generated uniformly from the permutations of a given length, and a un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Efficiency (statistics)
In statistics, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator, needs fewer input data or observations than a less efficient one to achieve the Cramér–Rao bound. An ''efficient estimator'' is characterized by having the smallest possible variance, indicating that there is a small deviance between the estimated value and the "true" value in the L2 norm sense. The relative efficiency of two procedures is the ratio of their efficiencies, although often this concept is used where the comparison is made between a given procedure and a notional "best possible" procedure. The efficiencies and the relative efficiency of two procedures theoretically depend on the sample size available for the given procedure, but it is often possible to use the asymptotic relative efficiency (defined as the limit of the relative efficiencies as the sample size grows) as the principal comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platykurtic
In probability theory and statistics, kurtosis (from el, κυρτός, ''kyrtos'' or ''kurtos'', meaning "curved, arching") is a measure of the "tailedness" of the probability distribution of a real number, real-valued random variable. Like skewness, kurtosis describes a particular aspect of a probability distribution. There are different ways to quantify kurtosis for a theoretical distribution, and there are corresponding ways of estimating it using a sample from a population. Different measures of kurtosis may have different #Interpretation, interpretations. The standard measure of a distribution's kurtosis, originating with Karl Pearson, is a scaled version of the fourth moment (mathematics), moment of the distribution. This number is related to the tails of the distribution, not its peak; hence, the sometimes-seen characterization of kurtosis as "peakedness" is incorrect. For this measure, higher kurtosis corresponds to greater extremity of Deviation (statistics), deviations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deciles
In descriptive statistics, a decile is any of the nine values that divide the sorted data into ten equal parts, so that each part represents 1/10 of the sample or population. A decile is one possible form of a quantile; others include the quartile In statistics, a quartile is a type of quantile which divides the number of data points into four parts, or ''quarters'', of more-or-less equal size. The data must be ordered from smallest to largest to compute quartiles; as such, quartiles are a ... and percentile.. A decile rank arranges the data in order from lowest to highest and is done on a scale of one to ten where each successive number corresponds to an increase of 10 percentage points. Special Usage: The decile mean A moderately robust measure of central tendency - known as the decile mean - can be computed by making use of a sample's deciles D_ to D_ (D_ = 10th percentile, D_ = 20th percentile and so on). It is calculated as follows: : DM = \frac Apart from serving ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Estimators
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule (the estimator), the quantity of interest (the estimand) and its result (the estimate) are distinguished. For example, the sample mean is a commonly used estimator of the population mean. There are point and interval estimators. The point estimators yield single-valued results. This is in contrast to an interval estimator, where the result would be a range of plausible values. "Single value" does not necessarily mean "single number", but includes vector valued or function valued estimators. ''Estimation theory'' is concerned with the properties of estimators; that is, with defining properties that can be used to compare different estimators (different rules for creating estimates) for the same quantity, based on the same data. Such properties can be used to determine the best rules to use under given circumstances. However, in robust statistics, statisti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |