|
Sammon's Mapping
Sammon mapping or Sammon projection is an algorithm that maps a high-dimensional space to a space of lower dimensionality (see multidimensional scaling) by trying to preserve the structure of inter-point distances in high-dimensional space in the lower-dimension projection. It is particularly suited for use in exploratory data analysis. The method was proposed by John W. Sammon in 1969. It is considered a non-linear approach as the mapping cannot be represented as a linear combination of the original variables as possible in techniques such as principal component analysis, which also makes it more difficult to use for classification applications. Denote the distance between ith and jth objects in the original space by \scriptstyle d^_, and the distance between their projections by \scriptstyle d^_. Sammon's mapping aims to minimize the following error function, which is often referred to as Sammon's stress or Sammon's error: :E = \frac\sum_\frac. The minimization can be perfo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map (mathematics)
In mathematics, a map or mapping is a function in its general sense. These terms may have originated as from the process of making a geographical map: ''mapping'' the Earth surface to a sheet of paper. The term ''map'' may be used to distinguish some special types of functions, such as homomorphisms. For example, a linear map is a homomorphism of vector spaces, while the term linear function may have this meaning or it may mean a linear polynomial. In category theory, a map may refer to a morphism. The term ''transformation'' can be used interchangeably, but ''transformation'' often refers to a function from a set to itself. There are also a few less common uses in logic and graph theory. Maps as functions In many branches of mathematics, the term ''map'' is used to mean a function, sometimes with a specific property of particular importance to that branch. For instance, a "map" is a " continuous function" in topology, a "linear transformation" in linear algebra, etc. Some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multidimensional Scaling
Multidimensional scaling (MDS) is a means of visualizing the level of similarity of individual cases of a dataset. MDS is used to translate "information about the pairwise 'distances' among a set of n objects or individuals" into a configuration of n points mapped into an abstract Cartesian space. More technically, MDS refers to a set of related ordination techniques used in information visualization, in particular to display the information contained in a distance matrix. It is a form of non-linear dimensionality reduction. Given a distance matrix with the distances between each pair of objects in a set, and a chosen number of dimensions, ''N'', an MDS algorithm places each object into ''N''-dimensional space (a lower-dimensional representation) such that the between-object distances are preserved as well as possible. For ''N'' = 1, 2, and 3, the resulting points can be visualized on a scatter plot. Core theoretical contributions to MDS were made by James O. Ramsay of M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exploratory Data Analysis
In statistics, exploratory data analysis (EDA) is an approach of analyzing data sets to summarize their main characteristics, often using statistical graphics and other data visualization methods. A statistical model can be used or not, but primarily EDA is for seeing what the data can tell us beyond the formal modeling and thereby contrasts traditional hypothesis testing. Exploratory data analysis has been promoted by John Tukey since 1970 to encourage statisticians to explore the data, and possibly formulate hypotheses that could lead to new data collection and experiments. EDA is different from initial data analysis (IDA), which focuses more narrowly on checking assumptions required for model fitting and hypothesis testing, and handling missing values and making transformations of variables as needed. EDA encompasses IDA. Overview Tukey defined data analysis in 1961 as: "Procedures for analyzing data, techniques for interpreting the results of such procedures, ways of pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Component Analysis
Principal component analysis (PCA) is a popular technique for analyzing large datasets containing a high number of dimensions/features per observation, increasing the interpretability of data while preserving the maximum amount of information, and enabling the visualization of multidimensional data. Formally, PCA is a statistical technique for reducing the dimensionality of a dataset. This is accomplished by linearly transforming the data into a new coordinate system where (most of) the variation in the data can be described with fewer dimensions than the initial data. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identify clusters of closely related data points. Principal component analysis has applications in many fields such as population genetics, microbiome studies, and atmospheric science. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
In mathematics, gradient descent (also often called steepest descent) is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Haskell Curry in 1944, with the method becoming increasingly well-studied and used in the following decades. Description Gradient descent is based on the observation that if the multi-variable function F(\mathbf) is def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
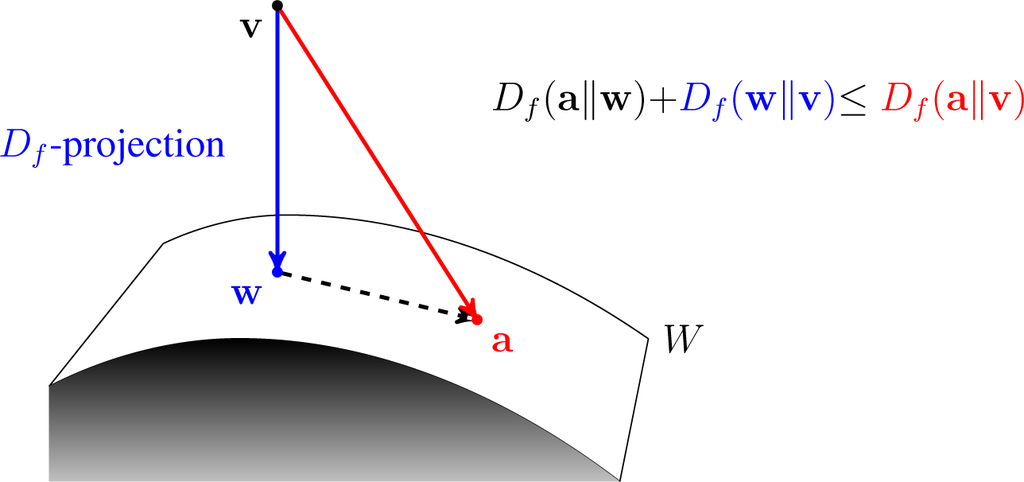
Bregman Divergence
In mathematics, specifically statistics and information geometry, a Bregman divergence or Bregman distance is a measure of difference between two points, defined in terms of a strictly convex function; they form an important class of divergences. When the points are interpreted as probability distributions – notably as either values of the parameter of a parametric model or as a data set of observed values – the resulting distance is a statistical distance. The most basic Bregman divergence is the squared Euclidean distance. Bregman divergences are similar to metrics, but satisfy neither the triangle inequality (ever) nor symmetry (in general). However, they satisfy a generalization of the Pythagorean theorem, and in information geometry the corresponding statistical manifold is interpreted as a (dually) flat manifold. This allows many techniques of optimization theory to be generalized to Bregman divergences, geometrically as generalizations of least squares. Bregman divergenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
State–action–reward–state–action
State–action–reward–state–action (SARSA) is an algorithm for learning a Markov decision process policy, used in the reinforcement learning area of machine learning. It was proposed by Rummery and Niranjan in a technical note with the name "Modified Connectionist Q-Learning" (MCQ-L). The alternative name SARSA, proposed by Rich Sutton, was only mentioned as a footnote. This name reflects the fact that the main function for updating the Q-value depends on the current state of the agent "S1", the action the agent chooses "A1", the reward "R" the agent gets for choosing this action, the state "S2" that the agent enters after taking that action, and finally the next action "A2" the agent chooses in its new state. The acronym for the quintuple (st, at, rt, st+1, at+1) is SARSA. Some authors use a slightly different convention and write the quintuple (st, at, rt+1, st+1, at+1), depending on which time step the reward is formally assigned. The rest of the article uses the former ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constructing Skill Trees
Constructing skill trees (CST) is a hierarchical reinforcement learning algorithm which can build skill trees from a set of sample solution trajectories obtained from demonstration. CST uses an incremental MAP (maximum a posteriori) change point detection algorithm to segment each demonstration trajectory into skills and integrate the results into a skill tree. CST was introduced by George Konidaris, Scott Kuindersma, Andrew Barto and Roderic Grupen in 2010. Algorithm CST consists of mainly three parts;change point detection, alignment and merging. The main focus of CST is online change-point detection. The change-point detection algorithm is used to segment data into skills and uses the sum of discounted reward R_t as the target regression variable. Each skill is assigned an appropriate abstraction. A particle filter is used to control the computational complexity of CST. The change point detection algorithm is implemented as follows. The data for times t\in T and models w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functions And Mappings
In mathematics, a map or mapping is a function in its general sense. These terms may have originated as from the process of making a geographical map: ''mapping'' the Earth surface to a sheet of paper. The term ''map'' may be used to distinguish some special types of functions, such as homomorphisms. For example, a linear map is a homomorphism of vector spaces, while the term linear function may have this meaning or it may mean a linear polynomial. In category theory, a map may refer to a morphism. The term ''transformation'' can be used interchangeably, but ''transformation'' often refers to a function from a set to itself. There are also a few less common uses in logic and graph theory. Maps as functions In many branches of mathematics, the term ''map'' is used to mean a function, sometimes with a specific property of particular importance to that branch. For instance, a "map" is a "continuous function" in topology, a "linear transformation" in linear algebra, etc. Some au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |