|
SABR Volatility Model
In mathematical finance, the SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "stochastic alpha, beta, rho", referring to the parameters of the model. The SABR model is widely used by practitioners in the financial industry, especially in the interest rate derivative markets. It was developed by Patrick S. Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward. Dynamics The SABR model describes a single forward F, such as a LIBOR forward rate, a forward swap rate, or a forward stock price. This is one of the standards in market used by market participants to quote volatilities. The volatility of the forward F is described by a parameter \sigma. SABR is a dynamic model in which both F and \sigma are represented by stochastic state variables whose time evolution is given by the following system of stochastic differential equations: :dF_t=\sigma_t \left(F_t\right)^\beta\, dW_t, :d\sigma_t=\a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often by help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on mathematical fina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black Model
The Black model (sometimes known as the Black-76 model) is a variant of the Black–Scholes option pricing model. Its primary applications are for pricing options on future contracts, bond options, interest rate cap and floors, and swaptions. It was first presented in a paper written by Fischer Black in 1976. Black's model can be generalized into a class of models known as log-normal forward models, also referred to as LIBOR market model. The Black formula The Black formula is similar to the Black–Scholes formula for valuing stock options except that the spot price of the underlying is replaced by a discounted futures price F. Suppose there is constant risk-free interest rate ''r'' and the futures price ''F(t)'' of a particular underlying is log-normal with constant volatility ''σ''. Then the Black formula states the price for a European call option of maturity ''T'' on a futures contract with strike price ''K'' and delivery date ''T (with T' \geq T) is : c = e^ N(d_1) - K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivatives (finance)
The derivative of a function is the rate of change of the function's output relative to its input value. Derivative may also refer to: In mathematics and economics *Brzozowski derivative in the theory of formal languages *Formal derivative, an operation on elements of a polynomial ring which mimics the form of the derivative from calculus * Radon–Nikodym derivative in measure theory *Derivative (set theory), a concept applicable to normal functions *Derivative (graph theory), an alternative term for a line graph deva *Derivative (finance), a contract whose value is derived from that of other quantities *Derivative suit or derivative action, a type of lawsuit filed by shareholders of a corporation In science and engineering *Derivative (chemistry), a type of compound which is a product of the process of derivatization *Derivative (linguistics), the process of forming a new word on the basis of an existing word, e.g. happiness and unhappy from happy * Aeroderivative gas turbine, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk-neutral Measure
In mathematical finance, a risk-neutral measure (also called an equilibrium measure, or ''equivalent martingale measure'') is a probability measure such that each share price is exactly equal to the discounted expectation of the share price under this measure. This is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market, a derivative's price is the discounted expected value of the future payoff under the unique risk-neutral measure. Such a measure exists if and only if the market is arbitrage-free. The easiest way to remember what the risk-neutral measure is, or to explain it to a probability generalist who might not know much about finance, is to realize that it is: # The probability measure of a transformed random variable. Typically this transformation is the utility function of the payoff. The risk-neutral measure would be the measure corresponding to an expectation of the payoff with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Volatility
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others. Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, models based on Black-Scholes assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile and skew, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
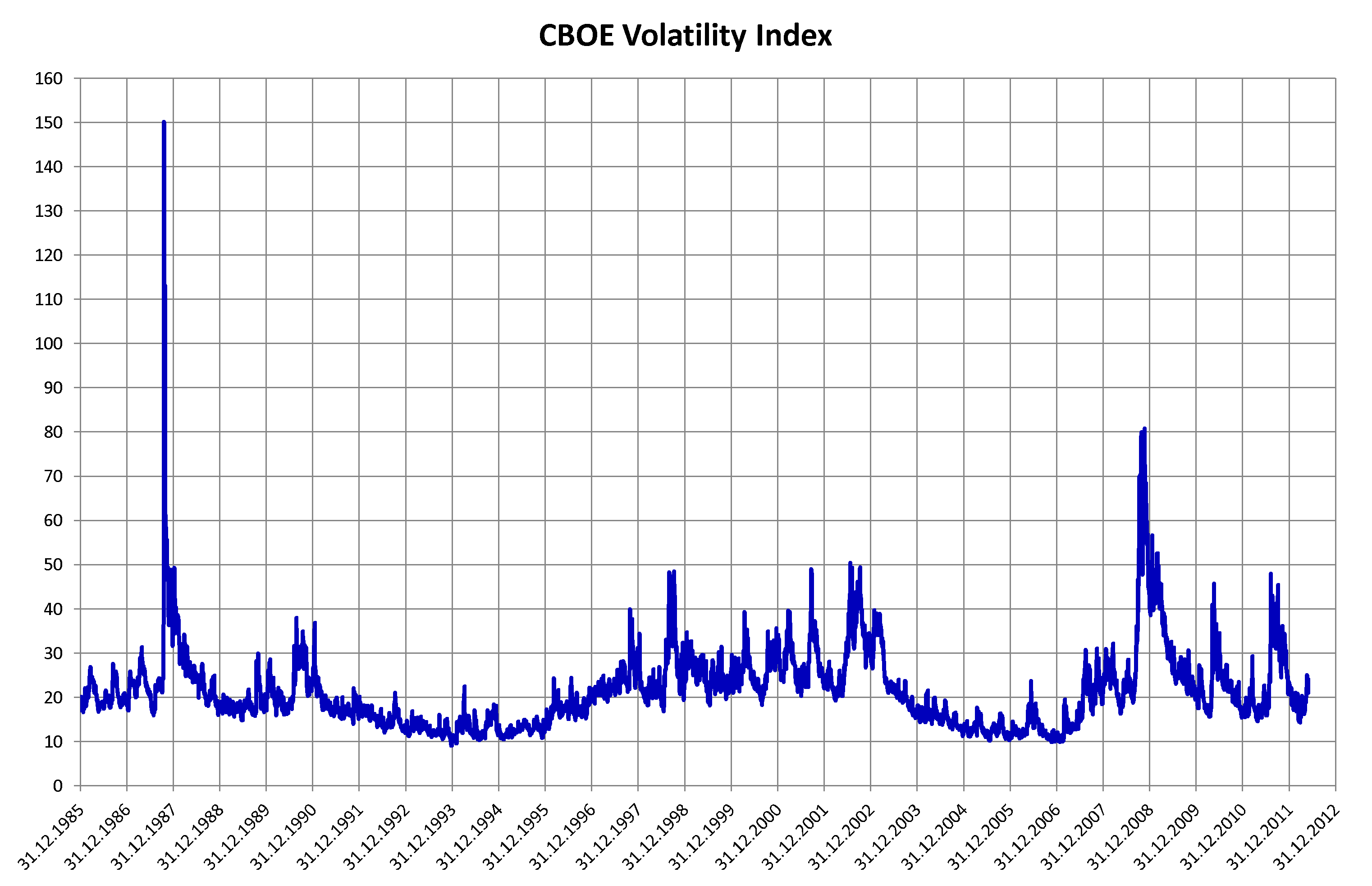
Volatility (finance)
In finance, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of squ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Futures Markets
''Journal of Futures Markets'' is a monthly peer-reviewed academic journal covers developments in financial futures and derivatives. The editor-in-chief is Robert Webb. The journal covers subjects including: futures, derivatives, risk management and control, financial engineering, new financial instruments, hedging strategies, analysis of trading systems, legal, accounting, and regulatory issues, and portfolio optimization. It is published by Wiley-Blackwell. According to the ''Journal Citation Reports'', its 2016 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as i ... is 1.291, ranking it 41 out of 96 journals in the category "Business, Finance". References External links * {{Official website, 1=http://onlinelibrary.wiley.com/journal/10.1002/(ISSN)1096-9934/homepag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Milstein Method
In mathematics, the Milstein method is a technique for the approximate numerical solution of a stochastic differential equation. It is named after Grigori N. Milstein who first published it in 1974. Description Consider the autonomous Itō stochastic differential equation: \mathrm X_t = a(X_t) \, \mathrm t + b(X_t) \, \mathrm W_t with initial condition X_ = x_, where W_ stands for the Wiener process, and suppose that we wish to solve this SDE on some interval of time ,T/math>. Then the Milstein approximation to the true solution X is the Markov chain Y defined as follows: * partition the interval ,T/math> into N equal subintervals of width \Delta t>0: 0 = \tau_0 < \tau_1 < \dots < \tau_N = T\text\tau_n:=n\Delta t\text\Delta t = \frac * set * recursively define for by: |
Euler–Maruyama Method
In Itô calculus, the Euler–Maruyama method (also called the Euler method) is a method for the approximate numerical solution of a stochastic differential equation (SDE). It is an extension of the Euler method for ordinary differential equations to stochastic differential equations. It is named after Leonhard Euler and Gisiro Maruyama. Unfortunately, the same generalization cannot be done for any arbitrary deterministic method. Consider the stochastic differential equation (see Itô calculus) :\mathrm X_t = a(X_t, t) \, \mathrm t + b(X_t, t) \, \mathrm W_t, with initial condition ''X''0 = ''x''0, where ''W''''t'' stands for the Wiener process, and suppose that we wish to solve this SDE on some interval of time , ''T'' Then the Euler–Maruyama approximation to the true solution ''X'' is the Markov chain ''Y'' defined as follows: * partition the interval , ''T''into ''N'' equal subintervals of width \Delta t>0: ::0 = \tau_ float: """ Sample a ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Brownian Motion
A geometric Brownian motion (GBM) (also known as exponential Brownian motion) is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion (also called a Wiener process) with drift. It is an important example of stochastic processes satisfying a stochastic differential equation (SDE); in particular, it is used in mathematical finance to model stock prices in the Black–Scholes model. Technical definition: the SDE A stochastic process ''S''''t'' is said to follow a GBM if it satisfies the following stochastic differential equation (SDE): : dS_t = \mu S_t\,dt + \sigma S_t\,dW_t where W_t is a Wiener process or Brownian motion, and \mu ('the percentage drift') and \sigma ('the percentage volatility') are constants. The former is used to model deterministic trends, while the latter term is often used to model a set of unpredictable events occurring during this motion. Solving the SDE For an arbitrary initial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Journal Of Theoretical And Applied Finance
The ''International Journal of Theoretical and Applied Finance'' was founded in 1998 and is published by World Scientific. It covers the use of quantitative tools in finance, including articles on development and simulation of mathematical models, their industrial usage, and application of modern stochastic methods. Abstracting and indexing The journal is abstracted and indexed in: * JEL electronic indexes, includes EconList, e-JEL, and JEL on CD * Social Science Research Network (SSRN) * Mathematical Reviews * The CFA Digest * CSA Risk Abstracts * International Bibliography of the Social Sciences * Zentralblatt MATH zbMATH Open, formerly Zentralblatt MATH, is a major reviewing service providing reviews and abstracts for articles in pure and applied mathematics, produced by the Berlin office of FIZ Karlsruhe – Leibniz Institute for Information Infrastruct ... * Inspec Finance journals Publications established in 1998 World Scientific academic journals English-languag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Interest Rates
An interest rate is the amount of interest due per period, as a proportion of the amount lent, deposited, or borrowed (called the principal sum). The total interest on an amount lent or borrowed depends on the principal sum, the interest rate, the compounding frequency, and the length of time over which it is lent, deposited, or borrowed. The annual interest rate is the rate over a period of one year. Other interest rates apply over different periods, such as a month or a day, but they are usually annualized. The interest rate has been characterized as "an index of the preference . . . for a dollar of present ncomeover a dollar of future income." The borrower wants, or needs, to have money sooner rather than later, and is willing to pay a fee—the interest rate—for that privilege. Influencing factors Interest rates vary according to: * the government's directives to the central bank to accomplish the government's goals * the currency of the principal sum lent or borrowed * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
