|
Swaption
A swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps. Types There are two types of swaption contracts (analogous to put and call options): *A payer swaption gives the owner of the swaption the right to enter into a swap where they pay the fixed leg and receive the floating leg. *A receiver swaption gives the owner of the swaption the right to enter into a swap in which they will receive the fixed leg, and pay the floating leg. In addition, a "straddle" refers to a combination of a receiver and a payer option on the same underlying swap. The buyer and seller of the swaption agree on: *The premium (price) of the swaption *Length of the option period (which usually ends two business days prior to the start date of the underlying swap), *The terms of the underlying swap, including: **Notional amount (wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bermudan Option
In finance, the style or family of an option is the class into which the option falls, usually defined by the dates on which the option may be exercised. The vast majority of options are either European or American (style) options. These options—as well as others where the payoff is calculated similarly—are referred to as " vanilla options". Options where the payoff is calculated differently are categorized as "exotic options". Exotic options can pose challenging problems in valuation and hedging. American and European options The key difference between American and European options relates to when the options can be exercised: * A European option may be exercised only at the expiration date of the option, i.e. at a single pre-defined point in time. * An American option on the other hand may be exercised at any time before the expiration date. For both, the payoff—when it occurs—is given by * \max\, for a call option * \max\, for a put option where K is the strike ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hull–White Model
In financial mathematics, the Hull–White model is a model of future interest rates. In its most generic formulation, it belongs to the class of no-arbitrage models that are able to fit today's term structure of interest rates. It is relatively straightforward to translate the mathematical description of the evolution of future interest rates onto a tree or lattice and so interest rate derivatives such as bermudan swaptions can be valued in the model. The first Hull–White model was described by John C. Hull and Alan White in 1990. The model is still popular in the market today. The model One-factor model The model is a short-rate model. In general, it has the following dynamics: :dr(t) = \left theta(t) - \alpha(t) r(t)\right,dt + \sigma(t)\, dW(t). There is a degree of ambiguity among practitioners about exactly which parameters in the model are time-dependent or what name to apply to the model in each case. The most commonly accepted naming convention is the following: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Model (finance)
In quantitative finance, a lattice model is a numerical approach to the valuation of derivatives in situations requiring a discrete time model. For dividend paying equity options, a typical application would correspond to the pricing of an American-style option, where a decision to exercise is allowed at the closing of any calendar day up to the maturity. A continuous model, on the other hand, such as the standard Black–Scholes one, would only allow for the valuation of European options, where exercise is limited to the option's maturity date. For interest rate derivatives lattices are additionally useful in that they address many of the issues encountered with continuous models, such as pull to par. The method is also used for valuing certain exotic options, because of path dependence in the payoff. Traditional Monte Carlo methods for option pricing fail to account for optimal decisions to terminate the derivative by early exercise, but some methods now exist for so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black Model
The Black model (sometimes known as the Black-76 model) is a variant of the Black–Scholes option pricing model. Its primary applications are for pricing options on future contracts, bond options, interest rate cap and floors, and swaptions. It was first presented in a paper written by Fischer Black in 1976. Black's model can be generalized into a class of models known as log-normal forward models. The Black formula The Black formula is similar to the Black–Scholes formula for valuing stock options except that the spot price of the underlying is replaced by a discounted futures price F. Suppose there is constant risk-free interest rate ''r'' and the futures price ''F(t)'' of a particular underlying is log-normal with constant volatility ''σ''. Then the Black formula states the price for a European call option of maturity ''T'' on a futures contract with strike price ''K'' and delivery date ''T (with T' \geq T) is : c = e^ N(d_1) - KN(d_2)/math> The corresponding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Underlying
In finance, a derivative is a contract between a buyer and a seller. The derivative can take various forms, depending on the transaction, but every derivative has the following four elements: # an item (the "underlier") that can or must be bought or sold, # a future act which must occur (such as a sale or purchase of the underlier), # a price at which the future transaction must take place, and # a future date by which the act (such as a purchase or sale) must take place. A derivative's value depends on the performance of the underlier, which can be a commodity (for example, corn or oil), a financial instrument (e.g. a stock or a bond), a price index, a currency, or an interest rate. Derivatives can be used to insure against price movements ( hedging), increase exposure to price movements for speculation, or get access to otherwise hard-to-trade assets or markets. Most derivatives are price guarantees. But some are based on an event or performance of an act rather than a pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Option (finance)
In finance, an option is a contract which conveys to its owner, the ''holder'', the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset (or contingent liability) and have a valuation that may depend on a complex relationship between underlying asset price, time until expiration, market volatility, the risk-free rate of interest, and the strike price of the option. Options may be traded between private parties in '' over-the-counter'' (OTC) transactions, or they may be exchange-traded in live, public markets in the form of standardized contracts. Definition and application An option is a contract that allows the holder the right to buy or sell an underlying asset or financia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Present Value
In economics and finance, present value (PV), also known as present discounted value (PDV), is the value of an expected income stream determined as of the date of valuation. The present value is usually less than the future value because money has interest-earning potential, a characteristic referred to as the time value of money, except during times of negative interest rates, when the present value will be equal or more than the future value. Time value can be described with the simplified phrase, "A dollar today is worth more than a dollar tomorrow". Here, 'worth more' means that its value is greater than tomorrow. A dollar today is worth more than a dollar tomorrow because the dollar can be invested and earn a day's worth of interest, making the total accumulate to a value more than a dollar by tomorrow. Interest can be compared to Renting, rent. Just as rent is paid to a landlord by a tenant without the ownership of the asset being transferred, interest is paid to a lender by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black–Derman–Toy Model
In mathematical finance Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field. In general, there exist two separate branches of finance that req ..., the Black–Derman–Toy model (BDT) is a popular short-rate model used in the pricing of bond options, swaptions and other interest rate derivatives; see . It is a one-factor model; that is, a single stochastic factor—the short rate—determines the future evolution of all interest rates. It was the first model to combine the mean reversion (finance), mean-reverting behaviour of the short rate with the log-normal distribution, and is still widely used. History The model was introduced by Fischer Black, Emanuel Derman, and Bill Toy. It was first developed for in-house use by Goldman Sachs in the 1980s and was published in the ''Financial Analysts Journal'' in 1990. A personal account of the development o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ho–Lee Model
In financial mathematics, the Ho-Lee model is a short-rate model widely used in the pricing of bond options, swaptions and other interest rate derivatives, and in modeling future interest rates. It was developed in 1986 by Thomas Ho and Sang Bin Lee. Under this model, the short rate follows a normal process: :dr_t = \theta_t\, dt + \sigma\, dW_t The model can be calibrated to market data by implying the form of \theta_t from market prices, meaning that it can exactly return the price of bonds comprising the yield curve. This calibration, and subsequent valuation of bond options, swaptions and other interest rate derivatives, is typically performed via a binomial lattice based model. Closed form valuations of bonds, and " Black-like" bond option formulae are also available.Graeme West, (2010)''Interest Rate Derivatives'', Financial Modelling Agency. As the model generates a symmetric ("bell shaped") distribution of rates in the future, negative rates are possible. Further, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
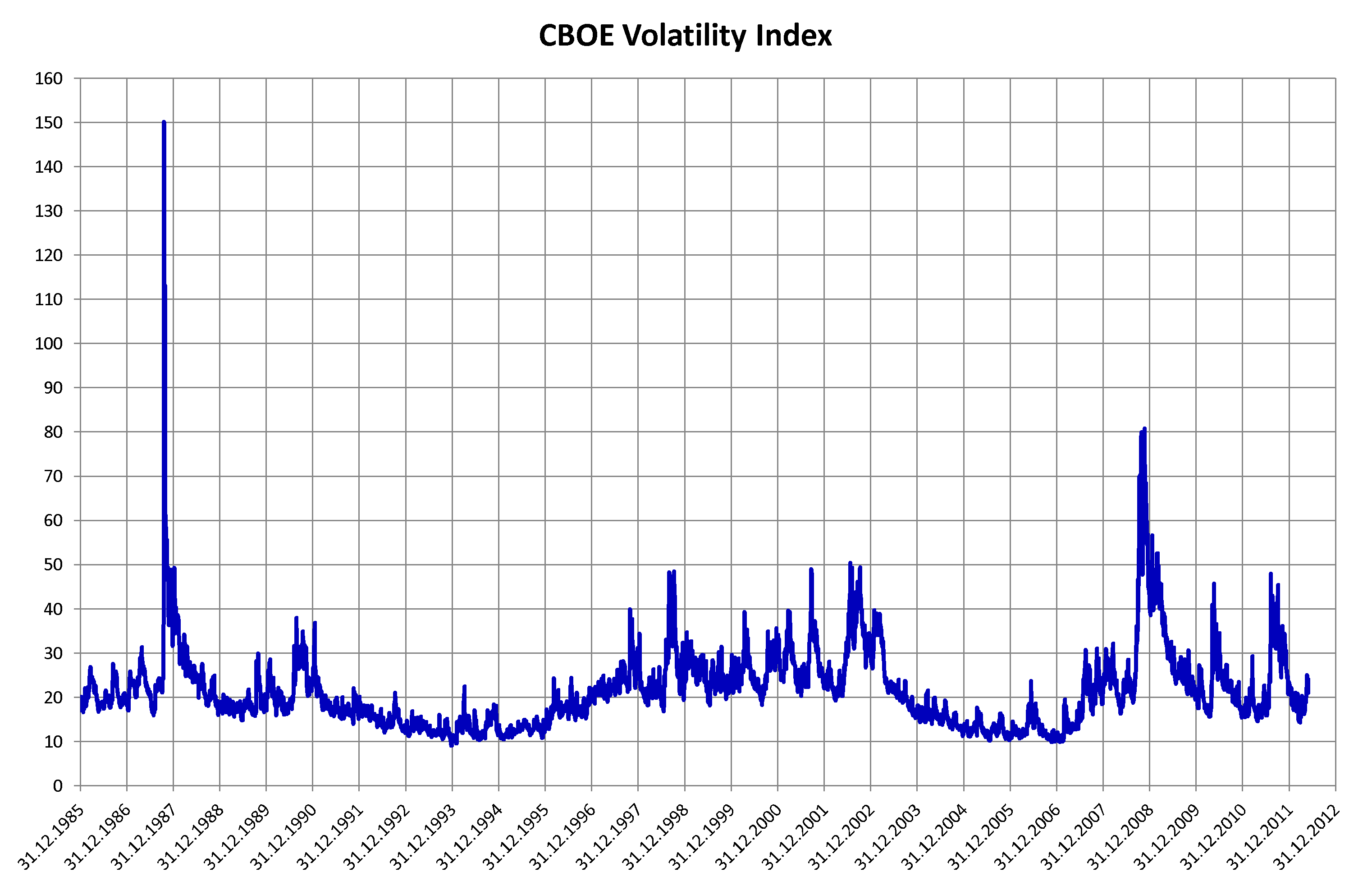
Volatility (finance)
In finance, volatility (usually denoted by "sigma, σ") is the Variability (statistics), degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |