|
Surface Evolver
Surface Evolver is an interactive program for the study of surfaces shaped by surface tension and other energies, and subject to various constraints. A surface is implemented as a simplicial complex. The user defines an initial surface in a datafile. The Evolver evolves the surface toward minimal energy by a gradient descent method. The aim can be to find a minimal energy surface, or to model the process of evolution by mean curvature. The energy in the Evolver can be a combination of surface tension, gravitational energy, squared mean curvature, user-defined surface integrals, or knot energies. The Evolver can handle arbitrary topology, volume constraints, boundary constraints, boundary contact angles, prescribed mean curvature, crystalline integrands, gravity, and constraints expressed as surface integrals. The surface can be in an ambient space of arbitrary dimension, which can have a Riemannian metric, and the ambient space can be a quotient space under a group action. Ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
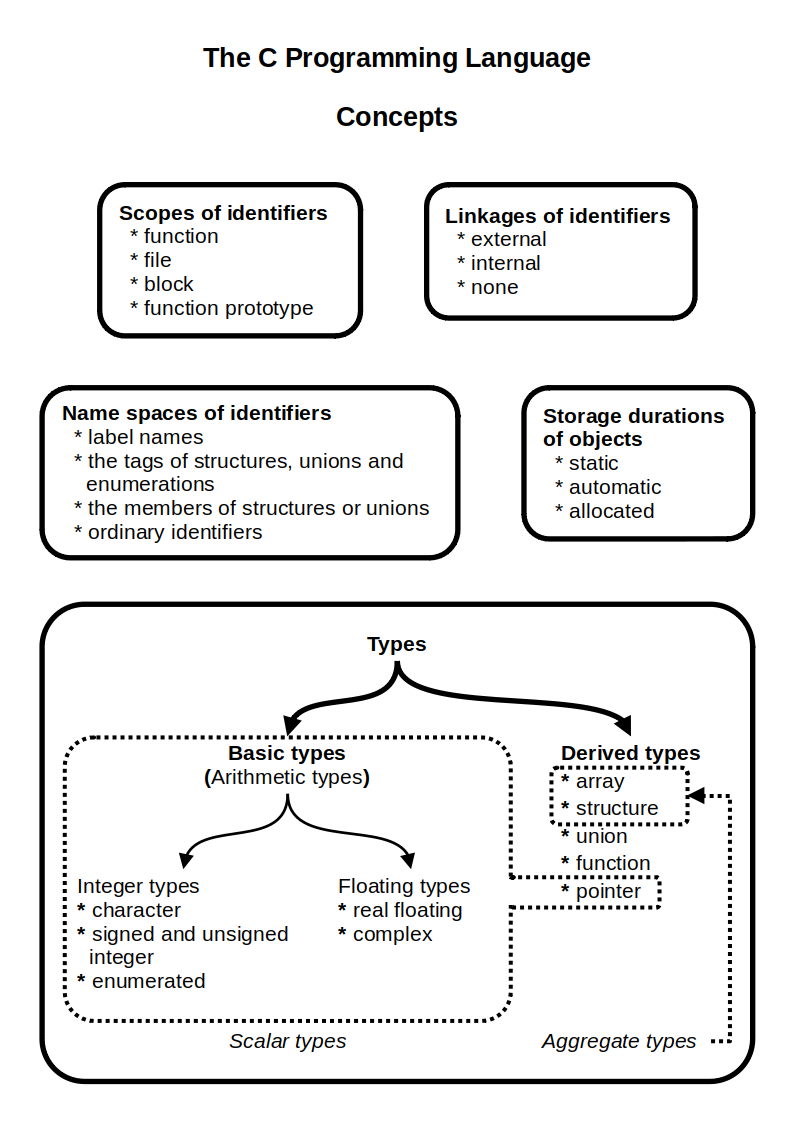
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Energy
In physical knot theory, a knot energy is a functional on the space of all knot conformations. A conformation of a knot is a particular embedding of a circle into three-dimensional space. Depending on the needs of the energy function, the space of conformations is restricted to a sufficiently nicely behaved class. For example, one may consider only polygonal circles or ''C''2 functions. A property of the functional often requires that evolution of the knot under gradient descent does not change knot type. Electrical charge The most common type of knot energy comes from the intuition of the knot as electrically charged. Coulomb's law states that two electric charges of the same sign will repel each other as the inverse square of the distance. Thus the knot will evolve under gradient descent according to the electric potential to an ideal configuration that minimizes the electrostatic energy. Naively defined, the integral for the energy will diverge and a regularization tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Minnesota
The University of Minnesota Twin Cities (historically known as University of Minnesota) is a public university, public Land-grant university, land-grant research university in the Minneapolis–Saint Paul, Twin Cities of Minneapolis and Saint Paul, Minnesota, United States. It is the Flagship#Colleges and universities in the United States, flagship institution of the University of Minnesota System and is organized into 19 colleges, schools, and other major academic units. The Twin Cities campus is the oldest and largest in the University of Minnesota system and has the List of United States university campuses by enrollment, ninth-largest (as of the 2022–2023 academic year) main campus student body in the United States, with 54,890 students at the start of the 2023–24 academic year. The campus comprises locations in Minneapolis and Falcon Heights, Minnesota, Falcon Heights, a suburb of St. Paul, approximately apart. The Minnesota Territorial Legislature drafted a charter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
United States Department Of Energy
The United States Department of Energy (DOE) is an executive department of the U.S. federal government that oversees U.S. national energy policy and energy production, the research and development of nuclear power, the military's nuclear weapons program, nuclear reactor production for the United States Navy, energy-related research, and energy conservation. The DOE was created in 1977 in the aftermath of the 1973 oil crisis. It sponsors more physical science research than any other U.S. federal agency, the majority of which is conducted through its system of National Laboratories. The DOE also directs research in genomics, with the Human Genome Project originating from a DOE initiative. The department is headed by the secretary of energy, who reports directly to the president of the United States and is a member of the Cabinet. The current secretary of energy is Chris Wright, who has served in the position since February 2025. The department's headquarters are in sou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
National Science Foundation
The U.S. National Science Foundation (NSF) is an Independent agencies of the United States government#Examples of independent agencies, independent agency of the Federal government of the United States, United States federal government that supports fundamental research and education in all the non-medical fields of science and engineering. Its medical counterpart is the National Institutes of Health. With an annual budget of about $9.9 billion (fiscal year 2023), the NSF funds approximately 25% of all federally supported basic research conducted by the List of American institutions of higher education, United States' colleges and universities. In some fields, such as mathematics, computer science, economics, and the social sciences, the NSF is the major source of federal backing. NSF's director and deputy director are appointed by the president of the United States and Advice and consent, confirmed by the United States Senate, whereas the 24 president-appointed members of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Geometry Center
The Geometry Center was a mathematics research and education center at the University of Minnesota. It was established by the National Science Foundation in the late 1980s and closed in 1998. The focus of the center's work was the use of computer graphics and Visualization (computer graphics), visualization for research and education in pure mathematics and geometry. The center's founding director was Albert Marden, Al Marden. Richard McGehee directed the center during its final years. The center's governing board was chaired by David P. Dobkin. Geomview Much of the work done at the center was for the development of Geomview, a three-dimensional interactive geometry software, interactive geometry program. This focused on mathematical visualization with options to allow hyperbolic space to be visualised. It was originally written for Silicon Graphics workstations, and has been ported to run on Linux systems; it is available for installation in most Linux distributions through the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Experimental Mathematics (journal)
''Experimental Mathematics'' is a quarterly scientific journal of mathematics published by A K Peters, Ltd. until 2010, now by Taylor & Francis. The journal publishes papers in experimental mathematics, broadly construed. The journal's mission statement describes its scope as follows: "Experimental Mathematics publishes original papers featuring formal results inspired by experimentation, conjectures suggested by experiments, and data supporting significant hypotheses." Its editor-in-chief is Alexander Kasprzyk (University of Nottingham). History ''Experimental Mathematics'' was established in 1992 by David Epstein, Silvio Levy, and Klaus Peters. ''Experimental Mathematics'' was the first mathematical research journal to concentrate on experimental mathematics and to explicitly acknowledge its importance for mathematics as a general research field. The journal's launching was described as "something of a watershed". Indeed, the launching of the journal in 1992 was surrounded by som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Action (mathematics)
In mathematics, a group action of a group G on a set (mathematics), set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S. Many sets of transformation (function), transformations form a group (mathematics), group under function composition; for example, the rotation (mathematics), rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a mathematical structure, structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles. If a group acts on a structure, it will usually also act on objects built from that st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Space (topology)
In topology and related areas of mathematics, the quotient space of a topological space under a given equivalence relation is a new topological space constructed by endowing the quotient set of the original topological space with the quotient topology, that is, with the finest topology that makes continuous the canonical projection map (the function that maps points to their equivalence classes). In other words, a subset of a quotient space is open if and only if its preimage under the canonical projection map is open in the original topological space. Intuitively speaking, the points of each equivalence class are or "glued together" for forming a new topological space. For example, identifying the points of a sphere that belong to the same diameter produces the projective plane as a quotient space. Definition Let X be a topological space, and let \sim be an equivalence relation on X. The quotient set Y = X/ is the set of equivalence classes of elements of X. The e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemannian Manifold
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as distance, angles, length, volume, and curvature are defined. Euclidean space, the N-sphere, n-sphere, hyperbolic space, and smooth surfaces in three-dimensional space, such as ellipsoids and paraboloids, are all examples of Riemannian manifold, manifolds. Riemannian manifolds are named after German mathematician Bernhard Riemann, who first conceptualized them. Formally, a Riemannian metric (or just a metric) on a smooth manifold is a choice of inner product for each tangent space of the manifold. A Riemannian manifold is a smooth manifold together with a Riemannian metric. The techniques of differential and integral calculus are used to pull geometric data out of the Riemannian metric. For example, integration leads to the Riemannian distance function, whereas differentiation is used to define curvature and parallel transport. Any smooth surface in three-dimensional Eucl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ambient Space
In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object along with the object itself. For example, a 1-dimensional line (l) may be studied in isolation —in which case the ambient space of l is l, or it may be studied as an object embedded in 2-dimensional Euclidean space (\mathbb^2)—in which case the ambient space of l is \mathbb^2, or as an object embedded in 2-dimensional hyperbolic space (\mathbb^2)—in which case the ambient space of l is \mathbb^2. To see why this makes a difference, consider the statement " Parallel lines never intersect." This is true if the ambient space is \mathbb^2, but false if the ambient space is \mathbb^2, because the geometric properties of \mathbb^2 are different from the geometric properties of \mathbb^2. All spaces are subsets of their ambient space. See also * Configuration space * Geometric space * Manifold and ambient manifold * Submanifolds and Hypersurfaces * R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |