|
Supertransitive Class
In set theory, a supertransitive class is a transitive class which includes as a subset the power set of each of its elements. Formally, let ''A'' be a transitive class. Then ''A'' is supertransitive if and only if :(\forall x)(x\in A \to \mathcal(x) \subseteq A). Here ''P''(''x'') denotes the power set of ''x''.''P''(''x'') must be a set by axiom of power set, since each element ''x'' of a class ''A'' must be a set (Theorem 4.6 in Takeuti's text above). See also * Transitive set * Rank (set theory) In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZF ... References {{reflist Set theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Theory
Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory, as a branch of mathematics, is mostly concerned with those that are relevant to mathematics as a whole. The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of '' naive set theory''. After the discovery of paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox) various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied. Set theory is commonly employed as a foundational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
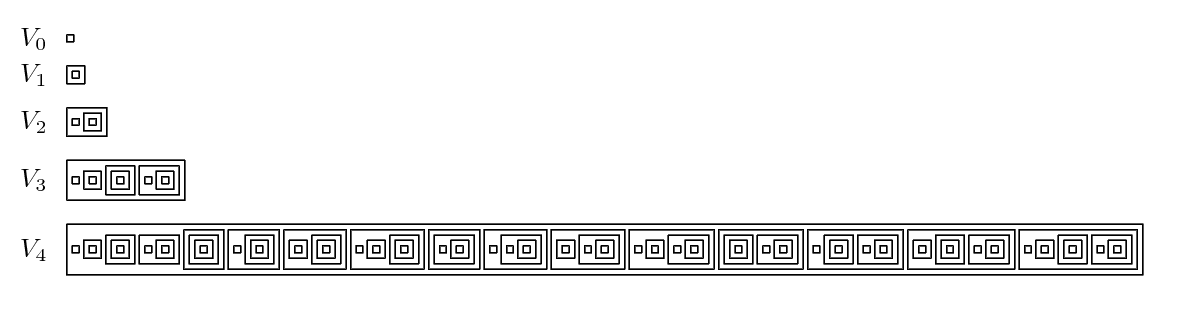
Transitive Set
In set theory, a branch of mathematics, a set A is called transitive if either of the following equivalent conditions hold: * whenever x \in A, and y \in x, then y \in A. * whenever x \in A, and x is not an urelement, then x is a subset of A. Similarly, a class M is transitive if every element of M is a subset of M. Examples Using the definition of ordinal numbers suggested by John von Neumann, ordinal numbers are defined as hereditarily transitive sets: an ordinal number is a transitive set whose members are also transitive (and thus ordinals). The class of all ordinals is a transitive class. Any of the stages V_\alpha and L_\alpha leading to the construction of the von Neumann universe V and Gödel's constructible universe L are transitive sets. The universes V and L themselves are transitive classes. This is a complete list of all finite transitive sets with up to 20 brackets: * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Set
In mathematics, the power set (or powerset) of a set is the set of all subsets of , including the empty set and itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is postulated by the axiom of power set. The powerset of is variously denoted as , , , \mathbb(S), or . The notation , meaning the set of all functions from S to a given set of two elements (e.g., ), is used because the powerset of can be identified with, equivalent to, or bijective to the set of all the functions from to the given two elements set. Any subset of is called a ''family of sets'' over . Example If is the set , then all the subsets of are * (also denoted \varnothing or \empty, the empty set or the null set) * * * * * * * and hence the power set of is . Properties If is a finite set with the cardinality (i.e., the number of all elements in the set is ), then the number of all the subsets of is . This fact as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Element (mathematics)
In mathematics, an element (or member) of a set is any one of the distinct objects that belong to that set. Sets Writing A = \ means that the elements of the set are the numbers 1, 2, 3 and 4. Sets of elements of , for example \, are subsets of . Sets can themselves be elements. For example, consider the set B = \. The elements of are ''not'' 1, 2, 3, and 4. Rather, there are only three elements of , namely the numbers 1 and 2, and the set \. The elements of a set can be anything. For example, C = \ is the set whose elements are the colors , and . Notation and terminology The relation "is an element of", also called set membership, is denoted by the symbol "∈". Writing :x \in A means that "''x'' is an element of ''A''". Equivalent expressions are "''x'' is a member of ''A''", "''x'' belongs to ''A''", "''x'' is in ''A''" and "''x'' lies in ''A''". The expressions "''A'' includes ''x''" and "''A'' contains ''x''" are also used to mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom Of Power Set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory. In the formal language of the Zermelo–Fraenkel axioms, the axiom reads: :\forall x \, \exists y \, \forall z \, \in y \iff \forall w \, (w \in z \Rightarrow w \in x)/math> where ''y'' is the Power set of ''x'', \mathcal(x). In English, this says: :Given any set ''x'', there is a set \mathcal(x) such that, given any set ''z'', this set ''z'' is a member of \mathcal(x) if and only if every element of ''z'' is also an element of ''x''. More succinctly: ''for every set x, there is a set \mathcal(x) consisting precisely of the subsets of x.'' Note the subset relation \subseteq is not used in the formal definition as subset is not a primitive relation in formal set theory; rather, subset is defined in terms of set membership, \in. By the axiom of extensionality, the set \mathcal(x) is unique. The axiom of power set appears in most axiomatizations of set theory. It is g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transitive Set
In set theory, a branch of mathematics, a set A is called transitive if either of the following equivalent conditions hold: * whenever x \in A, and y \in x, then y \in A. * whenever x \in A, and x is not an urelement, then x is a subset of A. Similarly, a class M is transitive if every element of M is a subset of M. Examples Using the definition of ordinal numbers suggested by John von Neumann, ordinal numbers are defined as hereditarily transitive sets: an ordinal number is a transitive set whose members are also transitive (and thus ordinals). The class of all ordinals is a transitive class. Any of the stages V_\alpha and L_\alpha leading to the construction of the von Neumann universe V and Gödel's constructible universe L are transitive sets. The universes V and L themselves are transitive classes. This is a complete list of all finite transitive sets with up to 20 brackets: * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (set Theory)
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930. The rank of a well-founded set is defined inductively as the smallest ordinal number greater than the ranks of all members of the set. In particular, the rank of the empty set is zero, and every ordinal has a rank equal to itself. The sets in ''V'' are divided into the transfinite hierarchy ''Vα'', called the cumulative hierarchy, based on their rank. Definition The cumulative hierarchy is a collection of sets ''V''α indexed by the class of ordinal numbers; in particular, ''V''α is the set of all sets having ranks less than α. Thus there is one set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |