|
Sum Of Absolute Deviations
Least absolute deviations (LAD), also known as least absolute errors (LAE), least absolute residuals (LAR), or least absolute values (LAV), is a statistical optimality criterion and a statistical optimization technique based minimizing the ''sum of absolute deviations'' (sum of absolute residuals or sum of absolute errors) or the ''L''1 norm of such values. It is analogous to the least squares technique, except that it is based on ''absolute values'' instead of squared values. It attempts to find a function which closely approximates a set of data by minimizing residuals between points generated by the function and corresponding data points. The LAD estimate also arises as the maximum likelihood estimate if the errors have a Laplace distribution. It was introduced in 1757 by Roger Joseph Boscovich. Formulation Suppose that the data set consists of the points (''x''''i'', ''y''''i'') with ''i'' = 1, 2, ..., ''n''. We want to find a function ''f'' such that f(x_i)\approx y_i. To ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimality Criterion
In statistics, an optimality criterion provides a measure of the fit of the data to a given hypothesis, to aid in model selection. A model is designated as the "best" of the candidate models if it gives the best value of an objective function measuring the degree of satisfaction of the criterion used to evaluate the alternative hypotheses. The term has been used to identify the different criteria that are used to evaluate a phylogenetic tree. For example, in order to determine the best topology between two phylogenetic trees using the maximum likelihood optimality criterion, one would calculate the maximum likelihood score of each tree and choose the one that had the better score. However, different optimality criteria can select different hypotheses. In such circumstances caution should be exercised when making strong conclusions. Many other disciplines use similar criteria or have specific measures geared toward the objectives of the field. Optimality criteria include maximum l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Program
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the optimization of a linear objective function, subject to linear equality and linear inequality constraints. Its feasible region is a convex polytope, which is a set defined as the intersection of finitely many half spaces, each of which is defined by a linear inequality. Its objective function is a real-valued affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polytope where this function has the smallest (or largest) value if such a point exists. Linear programs are problems that can be expressed in canonical form as : \begin & \text && \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lasso (statistics)
In statistics and machine learning, lasso (least absolute shrinkage and selection operator; also Lasso or LASSO) is a regression analysis method that performs both variable selection and regularization in order to enhance the prediction accuracy and interpretability of the resulting statistical model. It was originally introduced in geophysics, and later by Robert Tibshirani, who coined the term. Lasso was originally formulated for linear regression models. This simple case reveals a substantial amount about the estimator. These include its relationship to ridge regression and best subset selection and the connections between lasso coefficient estimates and so-called soft thresholding. It also reveals that (like standard linear regression) the coefficient estimates do not need to be unique if covariates are collinear. Though originally defined for linear regression, lasso regularization is easily extended to other statistical models including generalized linear models, generali ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, finance, computer science, particularly in machine learning and inverse problems, regularization is a process that changes the result answer to be "simpler". It is often used to obtain results for ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learning appr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Statistics & Data Analysis
''Computational Statistics & Data Analysis'' is a monthly peer-reviewed scientific journal covering research on and applications of computational statistics and data analysis. The journal was established in 1983 and is the official journal of the International Association for Statistical Computing, a section of the International Statistical Institute. See also *List of statistics journals This is a list of scientific journals published in the field of statistics. Introductory and outreach *''The American Statistician'' *'' Significance'' General theory and methodology *''Annals of the Institute of Statistical Mathematics'' *'' ... References External links * {{DEFAULTSORT:Computational Statistics And Data Analysis International Statistical Institute Statistics journals Publications established in 1983 Monthly journals English-language journals Elsevier academic journals * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, finance, computer science, particularly in machine learning and inverse problems, regularization is a process that changes the result answer to be "simpler". It is often used to obtain results for ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learning appr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median Regression , an algorithm for robust linear regression
{{disambig ...
Median regression may refer to: * Quantile regression, a regression analysis used to estimate conditional quantiles such as the median * Repeated median regression In robust statistics, repeated median regression, also known as the repeated median estimator, is a robust linear regression algorithm. The estimator has a breakdown point of 50%. Although it is equivariant under scaling, or under linear transforma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantile Regression
Quantile regression is a type of regression analysis used in statistics and econometrics. Whereas the method of least squares estimates the conditional ''mean'' of the response variable across values of the predictor variables, quantile regression estimates the conditional ''median'' (or other '' quantiles'') of the response variable. Quantile regression is an extension of linear regression used when the conditions of linear regression are not met. Advantages and applications One advantage of quantile regression relative to ordinary least squares regression is that the quantile regression estimates are more robust against outliers in the response measurements. However, the main attraction of quantile regression goes beyond this and is advantageous when conditional quantile functions are of interest. Different measures of central tendency and statistical dispersion can be useful to obtain a more comprehensive analysis of the relationship between variables. In ecology, quantile ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
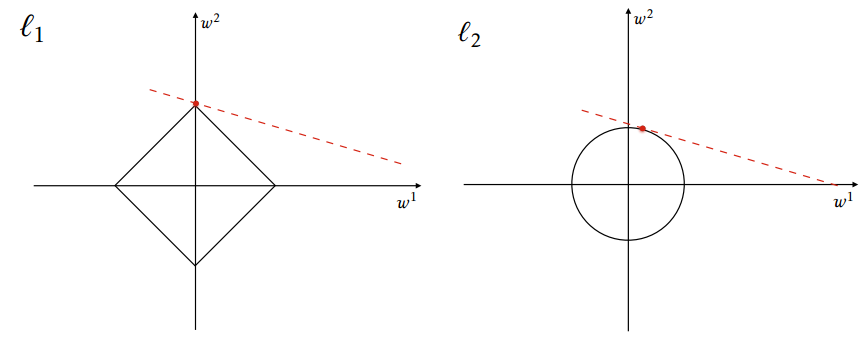
Least Absolute Deviations Regression Method Diagram
Comparison is a feature in the morphology or syntax of some languages whereby adjectives and adverbs are inflected to indicate the relative degree of the property they define exhibited by the word or phrase they modify or describe. In languages that have it, the comparative construction expresses quality, quantity, or degree relative to ''some'' other comparator(s). The superlative construction expresses the greatest quality, quantity, or degree—i.e. relative to ''all'' other comparators. The associated grammatical category is degree of comparison. The usual degrees of comparison are the ''positive'', which simply denotes a property (as with the English words ''big'' and ''fully''); the ''comparative'', which indicates ''greater'' degree (as ''bigger'' and ''more fully''); and the ''superlative'', which indicates ''greatest'' degree (as ''biggest'' and ''most fully''). Some languages have forms indicating a very large degree of a particular quality (called ''elative'' in Semiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomical Journal
''The Astronomical Journal'' (often abbreviated ''AJ'' in scientific papers and references) is a peer-reviewed monthly scientific journal owned by the American Astronomical Society (AAS) and currently published by IOP Publishing. It is one of the premier journals for astronomy in the world. Until 2008, the journal was published by the University of Chicago Press on behalf of the AAS. The reasons for the change to the IOP were given by the society as the desire of the University of Chicago Press to revise its financial arrangement and their plans to change from the particular software that had been developed in-house. The other two publications of the society, the ''Astrophysical Journal'' and its supplement series, followed in January 2009. The journal was established in 1849 by Benjamin A. Gould. It ceased publication in 1861 due to the American Civil War, but resumed in 1885. Between 1909 and 1941 the journal was edited in Albany, New York. In 1941, editor Benjamin Boss arranged ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent And Independent Variables
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called an in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Worcester Polytechnic Institute
'' , mottoeng = "Theory and Practice" , established = , former_name = Worcester County Free Institute of Industrial Science (1865-1886) , type = Private research university , endowment = $505.5 million (2020) , accreditation = NECHE , president = Winston Wole Soboyejo (interim) , provost = Arthur Heinricher (interim) , undergrad = 4,177 , postgrad = 1,962 , city = Worcester , state = Massachusetts , country = United States , campus = Midsize City, , athletics_affiliations = , sports_nickname = Engineers , mascot = Gompei the Goat , website = , logo = WPI wordmark.png , logo_upright = .5 , faculty = 478 , coordinates = , colors = Crimson Gray , aca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
