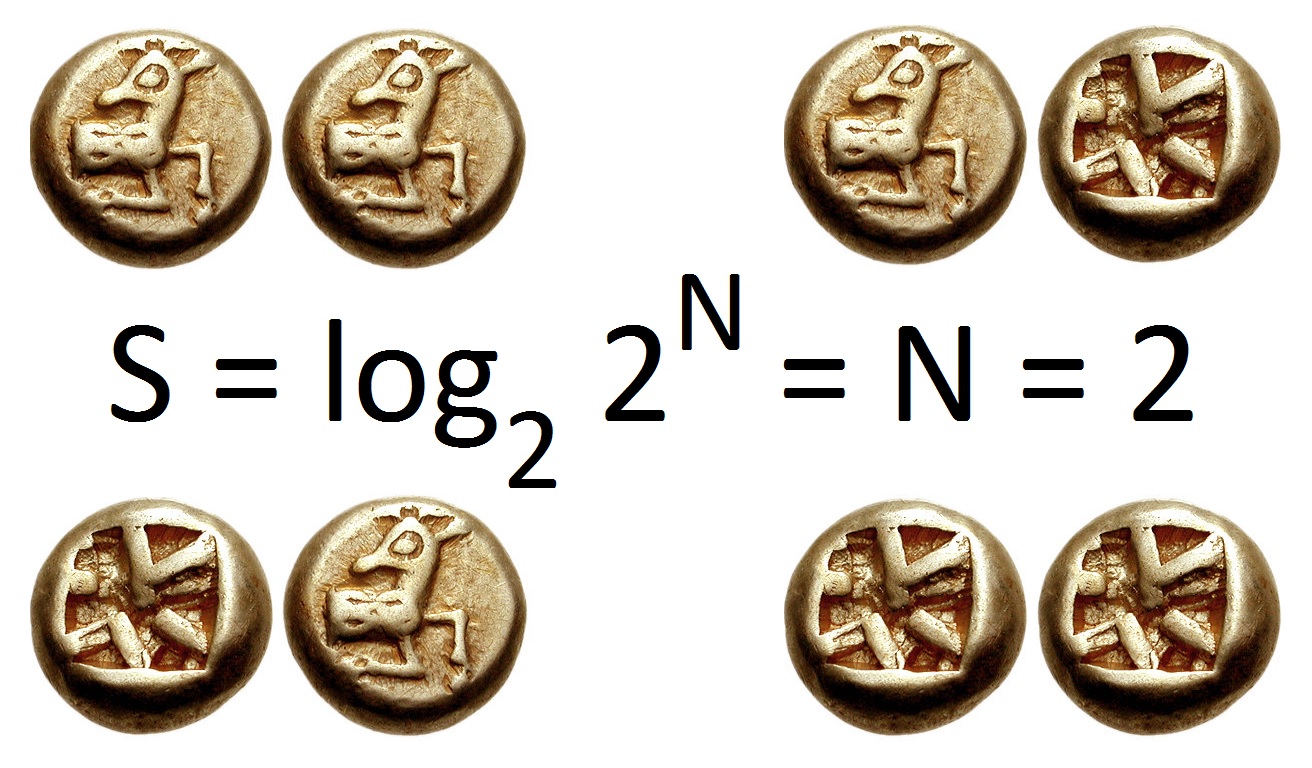|
Sudoku Code
Sudoku codes are non-linear forward error correcting codes following rules of sudoku puzzles designed for an erasure channel. Based on this model, the transmitter sends a sequence of all symbols of a solved sudoku. The receiver either receives a symbol correctly or an erasure symbol to indicate that the symbol was not received. The decoder gets a matrix with missing entries and uses the constraints of sudoku puzzles to reconstruct a limited amount of erased symbols. Sudoku codes are not suitable for practical usage but are subject of research. Questions like the rate and error performance are still unknown for general dimensions. In a sudoku one can find missing information by using different techniques to reproduce the full puzzle. This method can be seen as decoding a sudoku coded message that is sent over an erasure channel where some symbols got erased. By using the sudoku rules the decoder can recover the missing information. Sudokus can be modeled as a probabilistic graphic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forward Error Correction
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sudoku
Sudoku (; ja, 数独, sūdoku, digit-single; originally called Number Place) is a logic-based, combinatorial number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid (also called "boxes", "blocks", or "regions") contain all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution. French newspapers featured variations of the Sudoku puzzles in the 19th century, and the puzzle has appeared since 1979 in puzzle books under the name Number Place. However, the modern Sudoku only began to gain widespread popularity in 1986 when it was published by the Japanese puzzle company Nikoli under the name Sudoku, meaning "single number". It first appeared in a U.S. newspaper, and then ''The Times'' (London), in 2004, thanks to the efforts of Wayne Gould, who devised a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Of Sudoku
The mathematics of Sudoku refers to the use of mathematics to study Sudoku puzzles to answer questions such as ''"How many filled Sudoku grids are there?"'', "''What is the minimal number of clues in a valid puzzle?''" and ''"In what ways can Sudoku grids be symmetric?"'' through the use of combinatorics and group theory. The analysis of Sudoku falls is generally divided between analyzing the properties of unsolved puzzles (such as the minimum possible number of given clues) and analyzing the properties of solved puzzles. Initial analysis was largely focused on enumerating solutions, with results first appearing in 2004. For classical Sudoku, the number of filled grids is 6,670,903,752,021,072,936,960 (), which reduces to 5,472,730,538 essentially different solutions under the validity preserving transformations. There are 26 types of symmetry, but they can only be found in about 0.005% of all filled grids. A puzzle with a unique solution must have at least 17 clues, and there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to , 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper "A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Low-density Parity-check Code
In information theory, a low-density parity-check (LDPC) code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel. An LDPC code is constructed using a sparse Tanner graph (subclass of the bipartite graph). LDPC codes are capacity-approaching codes, which means that practical constructions exist that allow the noise threshold to be set very close to the theoretical maximum (the Shannon limit) for a symmetric memoryless channel. The noise threshold defines an upper bound for the channel noise, up to which the probability of lost information can be made as small as desired. Using iterative belief propagation techniques, LDPC codes can be decoded in time linear to their block length. LDPC codes are finding increasing use in applications requiring reliable and highly efficient information transfer over bandwidth-constrained or return-channel-constrained links in the presence of corrupting noise. Implementation of LDPC codes has lag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factor Graph
A factor graph is a bipartite graph representing the factorization of a function. In probability theory and its applications, factor graphs are used to represent factorization of a probability distribution function, enabling efficient computations, such as the computation of marginal distributions through the sum-product algorithm. One of the important success stories of factor graphs and the sum-product algorithm is the decoding of capacity-approaching error-correcting codes, such as LDPC and turbo codes. Factor graphs generalize constraint graphs. A factor whose value is either 0 or 1 is called a constraint. A constraint graph is a factor graph where all factors are constraints. The max-product algorithm for factor graphs can be viewed as a generalization of the arc-consistency algorithm for constraint processing. Definition A factor graph is a bipartite graph representing the factorization of a function. Given a factorization of a function g(X_1,X_2,\dots,X_n), :g(X_1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tanner Graph
In coding theory, a Tanner graph, named after Michael Tanner, is a bipartite graph In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are ... used to state constraints or equations which specify error correcting codes. In coding theory, Tanner graphs are used to construct longer codes from smaller ones. Both encoders and decoders employ these graphs extensively. Origins Tanner graphs were proposed by Michael Tanner as a means to create larger error correcting codes from smaller ones using recursive techniques. He generalized the techniques of Elias for product codes. Tanner discussed lower bounds on the codes obtained from these graphs irrespective of the specific characteristics of the codes which were being used to construct larger codes. Tanner graphs for linear block codes Tan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dancing Links
In computer science, dancing links (DLX) is a technique for adding and deleting a node from a circular doubly linked list. It is particularly useful for efficiently implementing backtracking algorithms, such as Knuth's Algorithm X for the exact cover problem. Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem. Some of the better-known exact cover problems include tiling, the ''n'' queens problem, and Sudoku. The name ''dancing links'', which was suggested by Donald Knuth, stems from the way the algorithm works, as iterations of the algorithm cause the links to "dance" with partner links so as to resemble an "exquisitely choreographed dance." Knuth credits Hiroshi Hitotsumatsu and Kōhei Noshita with having invented the idea in 1979, but it is his paper which has popularized it. Implementation As the remainder of this article discusses the details of an implementation technique for Algorithm X, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sudoku Solving Algorithms
A standard Sudoku contains 81 cells, in a 9×9 grid, and has 9 boxes, each box being the intersection of the first, middle, or last 3 rows, and the first, middle, or last 3 columns. Each cell may contain a number from one to nine, and each number can only occur once in each row, column, and box. A Sudoku starts with some cells containing numbers (''clues''), and the goal is to solve the remaining cells. Proper Sudokus have one solution. Players and investigators use a wide range of computer algorithms to solve Sudokus, study their properties, and make new puzzles, including Sudokus with interesting symmetries and other properties. There are several computer algorithms that will solve 9×9 puzzles (=9) in fractions of a second, but combinatorial explosion occurs as increases, creating limits to the properties of Sudokus that can be constructed, analyzed, and solved as increases. Techniques Backtracking Some hobbyists have developed computer programs that will solve Sudoku p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
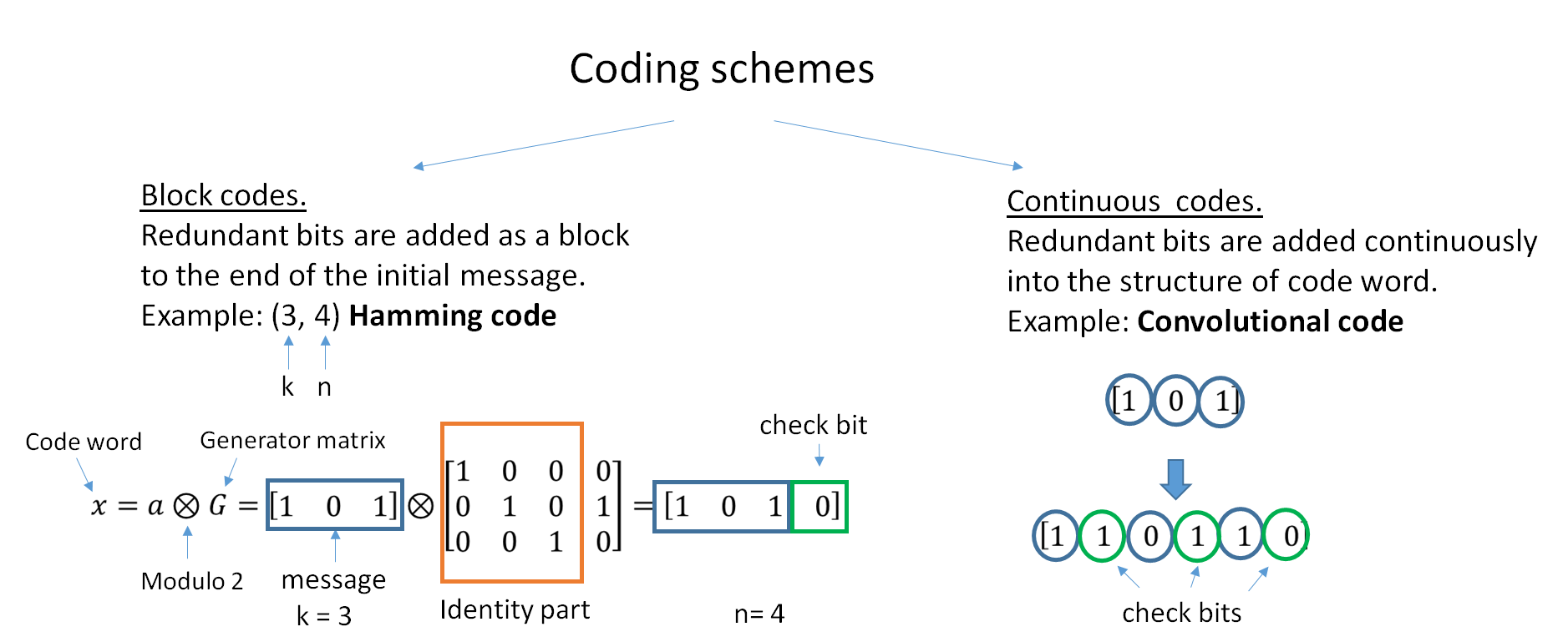
Linear Code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types. Linear codes allow for more efficient encoding and decoding algorithms than other codes (cf. syndrome decoding). Linear codes are used in forward error correction and are applied in methods for transmitting symbols (e.g., bits) on a communications channel so that, if errors occur in the communication, some errors can be corrected or detected by the recipient of a message block. The codewords in a linear block code are blocks of symbols that are encoded using more symbols than the original value to be sent. A linear code of length ''n'' transmits blocks containing ''n'' symbols. For example, the ,4,3 Hamming code is a linear binary code which represents 4-bit messages using 7-bit codewords. Two distinct c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png "Click for more on -> Mathematics Of Sudoku"){kind=spacer}
