|
Structured Data Analysis (statistics)
Structured data analysis is the statistical data analysis of structured data. This can arise either in the form of an ''a priori'' structure such as multiple-choice questionnaires or in situations with the need to search for structure that fits the given data, either exactly or approximately. This structure can then be used for making comparisons, predictions, manipulations etc. Types of structured data analysis * Algebraic data analysis *Bayesian analysis *Cluster analysis *Combinatorial data analysis * Formal concept analysis *Functional data analysis *Geometric data analysis *Regression analysis * Shape analysis *Topological data analysis In applied mathematics, topological based data analysis (TDA) is an approach to the analysis of datasets using techniques from topology. Extraction of information from datasets that are high-dimensional, incomplete and noisy is generally challengin ... * Tree structured data analysis References Further reading * * * Leland Wilkinson, ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structure
A structure is an arrangement and organization of interrelated elements in a material object or system, or the object or system so organized. Material structures include man-made objects such as buildings and machines and natural objects such as biological organisms, minerals and chemicals. Abstract structures include data structures in computer science and musical form. Types of structure include a hierarchy (a cascade of one-to-many relationships), a network featuring many-to-many links, or a lattice featuring connections between components that are neighbors in space. Load-bearing Buildings, aircraft, skeletons, anthills, beaver dams, bridges and salt domes are all examples of load-bearing structures. The results of construction are divided into buildings and non-building structures, and make up the infrastructure of a human society. Built structures are broadly divided by their varying design approaches and standards, into categories including building structures, arch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacqueline Meulman
Jacqueline Meulman (born 7 July 1954) is a Dutch statistician and professor emerita of Applied Statistics at the Mathematical Institute of Leiden University. Biography Born in The Hague, Meulman received her master's degree in mathematical psychology and data theory at Leiden University in 1981, and obtained her PhD in data theory in 1986 with the thesis entitled "A distance approach to nonlinear multivariate analysis" advised by Jan de Leeuw and John P. van de Geer. She was a consultant for Bell Telephone Laboratories in Murray Hill, NJ, from 1982 to 1983. In addition to being an associate professor in the Department of Data Theory in Leiden, she was an adjunct professor at the University of Illinois at Urbana–Champaign from 1993 to 1999. In 1998, she was appointed Professor of Applied Data Theory at Leiden University. Since 2009 she is Professor of Applied Statistics at the Mathematical Institute in Leiden. She is currently also an adjunct professor at the Department of St ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Analysis
Data analysis is a process of inspecting, cleansing, transforming, and modeling data with the goal of discovering useful information, informing conclusions, and supporting decision-making. Data analysis has multiple facets and approaches, encompassing diverse techniques under a variety of names, and is used in different business, science, and social science domains. In today's business world, data analysis plays a role in making decisions more scientific and helping businesses operate more effectively. Data mining is a particular data analysis technique that focuses on statistical modeling and knowledge discovery for predictive rather than purely descriptive purposes, while business intelligence covers data analysis that relies heavily on aggregation, focusing mainly on business information. In statistical applications, data analysis can be divided into descriptive statistics, exploratory data analysis (EDA), and confirmatory data analysis (CDA). EDA focuses on discovering ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hierarchical Bayes Model
Multilevel models (also known as hierarchical linear models, linear mixed-effect model, mixed models, nested data models, random coefficient, random-effects models, random parameter models, or split-plot designs) are statistical models of parameters that vary at more than one level. An example could be a model of student performance that contains measures for individual students as well as measures for classrooms within which the students are grouped. These models can be seen as generalizations of linear models (in particular, linear regression), although they can also extend to non-linear models. These models became much more popular after sufficient computing power and software became available. Multilevel models are particularly appropriate for research designs where data for participants are organized at more than one level (i.e., nested data). The units of analysis are usually individuals (at a lower level) who are nested within contextual/aggregate units (at a higher leve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cluster Analysis
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistics, statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis itself is not one specific algorithm, but the general task to be solved. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small Distance function, distances between cluster members, dense areas of the data space, intervals or particular statistical distributions. Clustering can therefore be formulated as a multi-object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Data Analysis
In statistics, combinatorial data analysis (CDA) is the study of data sets where the order in which objects are arranged is important. CDA can be used either to determine how well a given combinatorial construct reflects the observed data, or to search for a suitable combinatorial construct that does fit the data. See also * Cluster analysis *Geometric data analysis *Structured data analysis (statistics) Structured data analysis is the statistical data analysis of structured data. This can arise either in the form of an ''a priori'' structure such as multiple-choice questionnaires or in situations with the need to search for structure that fits t ... * Seriation (statistics) References Combinatorics Data analysis Combinatorial optimization {{statistics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
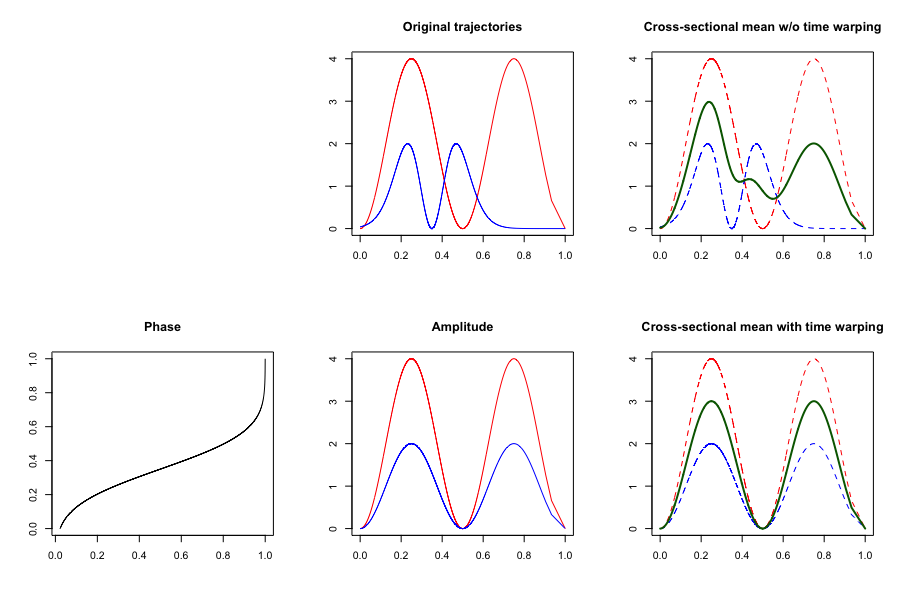
Functional Data Analysis
Functional data analysis (FDA) is a branch of statistics that analyses data providing information about curves, surfaces or anything else varying over a continuum. In its most general form, under an FDA framework, each sample element of functional data is considered to be a random function. The physical continuum over which these functions are defined is often time, but may also be spatial location, wavelength, probability, etc. Intrinsically, functional data are infinite dimensional. The high intrinsic dimensionality of these data brings challenges for theory as well as computation, where these challenges vary with how the functional data were sampled. However, the high or infinite dimensional structure of the data is a rich source of information and there are many interesting challenges for research and data analysis. History Functional data analysis has roots going back to work by Grenander and Karhunen in the 1940s and 1950s. They considered the decomposition of square-integrabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Data Analysis
Geometric data analysis comprises geometric aspects of image analysis, pattern analysis, and shape analysis, and the approach of multivariate statistics, which treat arbitrary data sets as ''clouds of points'' in a space that is ''n''-dimensional. This includes topological data analysis, cluster analysis, inductive data analysis, correspondence analysis, multiple correspondence analysis, principal components analysis and See also * Algebraic statistics for algebraic-geometry in statistics *Combinatorial data analysis *Computational anatomy for the study of shapes and forms at the morphome scale *Structured data analysis (statistics) Structured data analysis is the statistical data analysis of structured data. This can arise either in the form of an ''a priori'' structure such as multiple-choice questionnaires or in situations with the need to search for structure that fits t ... References * * Approximation of Geodesic Distances for Geometric Data Analysis Differential geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
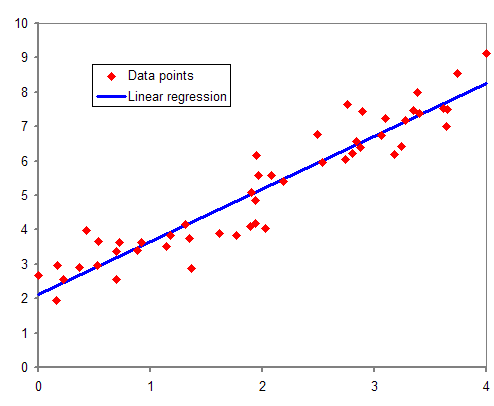
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Shape Analysis
Statistical shape analysis is an analysis of the geometrical properties of some given set of shapes by statistical methods. For instance, it could be used to quantify differences between male and female gorilla skull shapes, normal and pathological bone shapes, leaf outlines with and without herbivory by insects, etc. Important aspects of shape analysis are to obtain a measure of distance between shapes, to estimate mean shapes from (possibly random) samples, to estimate shape variability within samples, to perform clustering and to test for differences between shapes. One of the main methods used is principal component analysis (PCA). Statistical shape analysis has applications in various fields, including medical imaging, computer vision, computational anatomy, sensor measurement, and geographical profiling. Landmark-based techniques In the point distribution model, a shape is determined by a finite set of coordinate points, known as landmark points. These landmark points often ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
