|
Strategic Complementarities
In economics and game theory, the decisions of two or more players are called strategic complements if they mutually reinforce one another, and they are called strategic substitutes if they mutually offset one another. These terms were originally coined by Bulow, Geanakoplos, and Klemperer (1985). To see what is meant by 'reinforce' or 'offset', consider a situation in which the players all have similar choices to make, as in the paper of Bulow et al., where the players are all imperfectly competitive firms that must each decide how much to produce. Then the production decisions are strategic complements if an increase in the production of one firm increases the marginal revenues of the others, because that gives the others an incentive to produce more too. This tends to be the case if there are sufficiently strong aggregate increasing returns to scale and/or the demand curves for the firms' products have a sufficiently low own-price elasticity. On the other hand, the production de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economics
Economics () is the social science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services. Economics focuses on the behaviour and interactions of Agent (economics), economic agents and how economy, economies work. Microeconomics analyzes what's viewed as basic elements in the economy, including individual agents and market (economics), markets, their interactions, and the outcomes of interactions. Individual agents may include, for example, households, firms, buyers, and sellers. Macroeconomics analyzes the economy as a system where production, consumption, saving, and investment interact, and factors affecting it: employment of the resources of labour, capital, and land, currency inflation, economic growth, and public policies that have impact on glossary of economics, these elements. Other broad distinctions within economics include those between positive economics, desc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concave Function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex. Definition A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be ''concave'' if, for any x and y in the interval and for any \alpha \in ,1/math>, :f((1-\alpha )x+\alpha y)\geq (1-\alpha ) f(x)+\alpha f(y) A function is called ''strictly concave'' if :f((1-\alpha )x + \alpha y) > (1-\alpha) f(x) + \alpha f(y)\, for any \alpha \in (0,1) and x \neq y. For a function f: \mathbb \to \mathbb, this second definition merely states that for every z strictly between x and y, the point (z, f(z)) on the graph of f is above the straight line joining the points (x, f(x)) and (y, f(y)). A function f is quasiconcave if the upper contour sets of the function S(a)=\ are convex sets. Properties Functions of a single variable # A differentiab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplier (economics)
In macroeconomics, a multiplier is a factor of proportionality that measures how much an endogenous variable changes in response to a change in some exogenous variable. For example, suppose variable ''x'' changes by ''k'' units, which causes another variable ''y'' to change by ''M'' × ''k'' units. Then the multiplier is ''M''. Common uses Two multipliers are commonly discussed in introductory macroeconomics. Commercial banks create money, especially under the fractional-reserve banking system used throughout the world. In this system, money is created whenever a bank gives out a new loan. This is because the loan, when drawn on and spent, mostly finishes up as a deposit back in the banking system and is counted as part of money supply. After putting aside a part of these deposits as mandated bank reserves, the balance is available for the making of further loans by the bank. This process continues multiple times, and is called the multiplier effect. The multiplier may v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
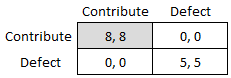
Coordination Failure (economics)
In economics, coordination failure is a concept that can explain recessions through the failure of firms and other price setters to coordinate. In an economic system with multiple equilibria, coordination failure occurs when a group of firms could achieve a more desirable equilibrium but fail to because they do not coordinate their decision making. Coordination failure can result in a self-fulfilling prophecy.Romer, 305. For example, if one firm decides a recession is imminent and fires its workers, other firms might lose demand from the lay-offs and respond by firing their own workers leading to a recession at a new equilibrium. Coordination failure can also be associated with sunspot equilibria (where equilibria are the result of variables that do not have any real impact on fundamentals) and animal spirits. Coordination failure can lead to an underemployment equilibrium. Coordination failure also implies that fiscal policy can mitigate the effects of recessions, or eve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
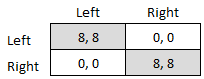
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-equilibrium combinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supermodular
In mathematics, a function :f\colon \mathbb^k \to \mathbb is supermodular if : f(x \uparrow y) + f(x \downarrow y) \geq f(x) + f(y) for all x, y \isin \mathbb^, where x \uparrow y denotes the componentwise maximum and x \downarrow y the componentwise minimum of x and y. If −''f'' is supermodular then ''f'' is called submodular, and if the inequality is changed to an equality the function is modular. If ''f'' is twice continuously differentiable, then supermodularity is equivalent to the condition : \frac \geq 0 \mbox i \neq j. Supermodularity in economics and game theory The concept of supermodularity is used in the social sciences to analyze how one agent's decision affects the incentives of others. Consider a symmetric game with a smooth payoff function \,f defined over actions \,z_i of two or more players i \in . Suppose the action space is continuous; for simplicity, suppose each action is chosen from an interval: z_i \in ,b/math>. In this context, supermodularity o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Submodular Set Function
In mathematics, a submodular set function (also known as a submodular function) is a set function whose value, informally, has the property that the difference in the incremental value of the function that a single element makes when added to an input set decreases as the size of the input set increases. Submodular functions have a natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory (as functions modeling user preferences) and electrical networks. Recently, submodular functions have also found immense utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains. Definition If \Omega is a finite set, a submodular function is a set function f:2^\rightarrow \mathbb, where 2^\Omega denotes the power set of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supermodular
In mathematics, a function :f\colon \mathbb^k \to \mathbb is supermodular if : f(x \uparrow y) + f(x \downarrow y) \geq f(x) + f(y) for all x, y \isin \mathbb^, where x \uparrow y denotes the componentwise maximum and x \downarrow y the componentwise minimum of x and y. If −''f'' is supermodular then ''f'' is called submodular, and if the inequality is changed to an equality the function is modular. If ''f'' is twice continuously differentiable, then supermodularity is equivalent to the condition : \frac \geq 0 \mbox i \neq j. Supermodularity in economics and game theory The concept of supermodularity is used in the social sciences to analyze how one agent's decision affects the incentives of others. Consider a symmetric game with a smooth payoff function \,f defined over actions \,z_i of two or more players i \in . Suppose the action space is continuous; for simplicity, suppose each action is chosen from an interval: z_i \in ,b/math>. In this context, supermodularity o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Game
In game theory, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. Symmetry can come in different varieties. Ordinally symmetric games are games that are symmetric with respect to the ordinal structure of the payoffs. A game is quantitatively symmetric if and only if it is symmetric with respect to the exact payoffs. A partnership game is a symmetric game where both players receive identical payoffs for any strategy set. That is, the payoff for playing strategy ''a'' against strategy ''b'' receives the same payoff as playing strategy ''b'' against strategy ''a''. Symmetry in 2x2 games Only 12 out of the 144 ordinally distinct 2x2 games are symmetric. However, many of the commonly studied 2x2 games are at least ordinally symmetric. The standard represent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-equilibrium combinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Equilibrium
In economics, general equilibrium theory attempts to explain the behavior of supply, demand, and prices in a whole economy with several or many interacting markets, by seeking to prove that the interaction of demand and supply will result in an overall general equilibrium. General equilibrium theory contrasts to the theory of ''partial'' equilibrium, which analyzes a specific part of an economy while its other factors are held constant. In general equilibrium, constant influences are considered to be noneconomic, therefore, resulting beyond the natural scope of economic analysis. The noneconomic influences is possible to be non-constant when the economic variables change, and the prediction accuracy may depend on the independence of the economic factors. General equilibrium theory both studies economies using the model of equilibrium pricing and seeks to determine in which circumstances the assumptions of general equilibrium will hold. The theory dates to the 1870s, particularly t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |