|
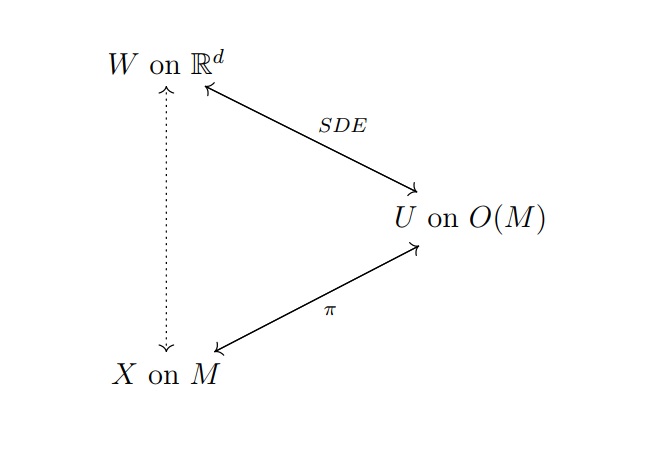
Stochastic Differential Geometry
In mathematics, stochastic analysis on manifolds or stochastic differential geometry is the study of Stochastic calculus, stochastic analysis over Differentiable manifold, smooth manifolds. It is therefore a synthesis of stochastic analysis (the extension of calculus to stochastic processes) and of differential geometry. The connection between Mathematical analysis, analysis and stochastic processes stems from the fundamental relation that the Infinitesimal generator (stochastic processes), infinitesimal generator of a continuous Strong Markov property, strong Markov chain, Markov process is a second-order Elliptic partial differential equation, elliptic operator. The infinitesimal generator of Brownian motion is the Laplace operator and the transition probability density p(t,x,y) of Brownian motion is the minimal heat kernel of the heat equation. Interpreting the paths of Brownian motion as Method of characteristics, characteristic curves of the operator, Brownian motion can be seen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes. This field was created and started by the Japanese people, Japanese mathematician Kiyosi Itô during World War II. The best-known stochastic process to which stochastic calculus is applied is the Wiener process (named in honor of Norbert Wiener), which is used for modeling Brownian motion as described by Louis Bachelier in 1900 and by Albert Einstein in 1905 and other physical diffusion processes in space of particles subject to random forces. Since the 1970s, the Wiener process has been widely applied in financial mathematics and economics to model the evolution in time of stock prices and bond interest rates. The main flavours of stochastic calculus are the Itô calculus and its variational relative the Malliavin calculus. For technical reasons the Itô integ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting local geometric objects, such as Tangent vector, tangent vectors or Tensor, tensors in the tangent space, along a curve or family of curves in a ''parallel'' and consistent manner. There are various kinds of connections in modern geometry, depending on what sort of data one wants to transport. For instance, an affine connection, the most elementary type of connection, gives a means for parallel transport of tangent space, tangent vectors on a manifold from one point to another along a curve. An affine connection is typically given in the form of a covariant derivative, which gives a means for taking directional derivatives of vector fields, measuring the deviation of a vector field from being parallel in a given direction. Connections are of central importance in modern geometry in large part because they allow a comparison between the local geometry at one point and the local geometry at another point. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hadamard Manifold
In mathematics, a Hadamard manifold, named after Jacques Hadamard — more often called a Cartan–Hadamard manifold, after Élie Cartan — is a Riemannian manifold (M, g) that is complete and simply connected and has everywhere non-positive sectional curvature. By Cartan–Hadamard theorem all Cartan–Hadamard manifolds are diffeomorphic to the Euclidean space \mathbb^n. Furthermore it follows from the Hopf–Rinow theorem that every pairs of points in a Cartan–Hadamard manifold may be connected by a unique geodesic segment. Thus Cartan–Hadamard manifolds are some of the closest relatives of \mathbb^n. Examples The Euclidean space \mathbb^n with its usual metric is a Cartan–Hadamard manifold with constant sectional curvature equal to 0. Standard n-dimensional hyperbolic space \mathbb^n is a Cartan–Hadamard manifold with constant sectional curvature equal to -1. Properties In Cartan-Hadamard manifolds, the map \exp_p : \operatornameM_p \to M is a diffeomorphism In m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Boundary Condition
In mathematics, the Dirichlet boundary condition is imposed on an ordinary or partial differential equation, such that the values that the solution takes along the boundary of the domain are fixed. The question of finding solutions to such equations is known as the Dirichlet problem. In the sciences and engineering, a Dirichlet boundary condition may also be referred to as a fixed boundary condition or boundary condition of the first type. It is named after Peter Gustav Lejeune Dirichlet (1805–1859). In finite-element analysis, the ''essential'' or Dirichlet boundary condition is defined by weighted-integral form of a differential equation. The dependent unknown ''u in the same form as the weight function w'' appearing in the boundary expression is termed a ''primary variable'', and its specification constitutes the ''essential'' or Dirichlet boundary condition. Examples ODE For an ordinary differential equation, for instance, y'' + y = 0, the Dirichlet boundary conditions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rolling Without Slipping
Rolling is a type of motion that combines rotation (commonly, of an axially symmetric object) and translation of that object with respect to a surface (either one or the other moves), such that, if ideal conditions exist, the two are in contact with each other without sliding. Rolling where there is no sliding is referred to as ''pure rolling''. By definition, there is no sliding when there is a frame of reference in which all points of contact on the rolling object have the same velocity as their counterparts on the surface on which the object rolls; in particular, for a frame of reference in which the rolling plane is at rest (see animation), the instantaneous velocity of all the points of contact (for instance, a generating line segment of a cylinder) of the rolling object is zero. In practice, due to small deformations near the contact area, some sliding and energy dissipation occurs. Nevertheless, the resulting rolling resistance is much lower than sliding friction, and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Brownian Motion
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frame Bundle
In mathematics, a frame bundle is a principal fiber bundle F(E) associated with any vector bundle ''E''. The fiber of F(E) over a point ''x'' is the set of all ordered bases, or ''frames'', for ''E_x''. The general linear group acts naturally on F(E) via a change of basis, giving the frame bundle the structure of a principal ''\mathrm(k,\mathbb)''-bundle (where ''k'' is the rank of ''E''). The frame bundle of a smooth manifold is the one associated with its tangent bundle. For this reason it is sometimes called the tangent frame bundle. Definition and construction Let ''E \to X'' be a real vector bundle of rank ''k'' over a topological space ''X''. A frame at a point ''x \in X'' is an ordered basis for the vector space ''E_x''. Equivalently, a frame can be viewed as a linear isomorphism :p : \mathbf^k \to E_x. The set of all frames at ''x'', denoted ''F_x'', has a natural right action by the general linear group ''\mathrm(k,\mathbb)'' of invertible ''k \times k'' matrices: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Horizontal Lift
In differential geometry, an Ehresmann connection (after the French mathematician Charles Ehresmann who first formalized this concept) is a version of the notion of a connection, which makes sense on any smooth fiber bundle. In particular, it does not rely on the possible vector bundle structure of the underlying fiber bundle, but nevertheless, linear connections may be viewed as a special case. Another important special case of Ehresmann connections are principal connections on principal bundles, which are required to be equivariant in the principal Lie group action. Introduction A covariant derivative in differential geometry is a linear differential operator which takes the directional derivative of a section of a vector bundle in a covariant manner. It also allows one to formulate a notion of a parallel section of a bundle in the direction of a vector: a section ''s'' is parallel along a vector X if \nabla_X s = 0. So a covariant derivative provides at least two things: a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semimartingale
In probability theory, a real-valued stochastic process ''X'' is called a semimartingale if it can be decomposed as the sum of a local martingale and a càdlàg adapted finite-variation process. Semimartingales are "good integrators", forming the largest class of processes with respect to which the Itô integral and the Stratonovich integral can be defined. The class of semimartingales is quite large (including, for example, all continuously differentiable processes, Brownian motion and Poisson processes). Submartingales and supermartingales together represent a subset of the semimartingales. Definition A real-valued process ''X'' defined on the filtered probability space (Ω,''F'',(''F''''t'')''t'' ≥ 0,P) is called a semimartingale if it can be decomposed as :X_t = M_t + A_t where ''M'' is a local martingale and ''A'' is a càdlàg adapted process of locally bounded variation. This means that for almost all \omega \in \Omega and all compact intervals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent Bundle
A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold M is a manifold TM which assembles all the tangent vectors in M . As a set, it is given by the disjoint unionThe disjoint union ensures that for any two points and of manifold the tangent spaces and have no common vector. This is graphically illustrated in the accompanying picture for tangent bundle of circle , see Examples section: all tangents to a circle lie in the plane of the circle. In order to make them disjoint it is necessary to align them in a plane perpendicular to the plane of the circle. of the tangent spaces of M . That is, : \begin TM &= \bigsqcup_ T_xM \\ &= \bigcup_ \left\ \times T_xM \\ &= \bigcup_ \left\ \\ &= \left\ \end where T_x M denotes the tangent space to M at the point x . So, an el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Differential Equation
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs have many applications throughout pure mathematics and are used to model various behaviours of stochastic models such as stock prices,Musiela, M., and Rutkowski, M. (2004), Martingale Methods in Financial Modelling, 2nd Edition, Springer Verlag, Berlin. random growth models or physical systems that are subjected to thermal fluctuations. SDEs have a random differential that is in the most basic case random white noise calculated as the distributional derivative of a Brownian motion or more generally a semimartingale. However, other types of random behaviour are possible, such as jump processes like Lévy processes or semimartingales with jumps. Stochastic differential equations are in general neither differential equations nor random differential equations. Random differential equation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |