|
Statistical Shape Model
Statistical shape analysis is an analysis of the geometrical properties of some given set of shapes by statistical methods. For instance, it could be used to quantify differences between male and female gorilla skull shapes, normal and pathological bone shapes, leaf outlines with and without herbivory by insects, etc. Important aspects of shape analysis are to obtain a measure of distance between shapes, to estimate mean shapes from (possibly random) samples, to estimate shape variability within samples, to perform clustering and to test for differences between shapes. One of the main methods used is principal component analysis (PCA). Statistical shape analysis has applications in various fields, including medical imaging, computer vision, computational anatomy, sensor measurement, and geographical profiling. Landmark-based techniques In the point distribution model, a shape is determined by a finite set of coordinate points, known as landmark points. These landmark points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
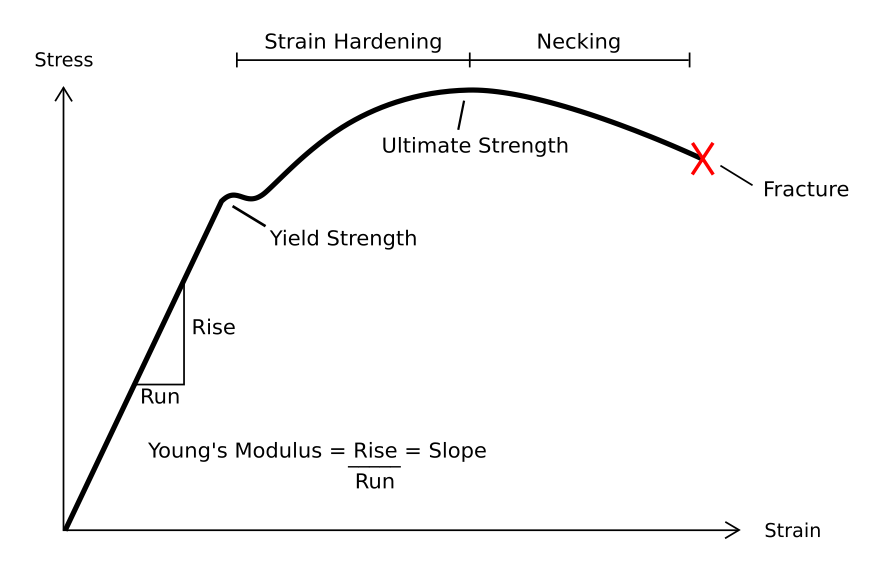
Deformation (engineering)
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a structure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
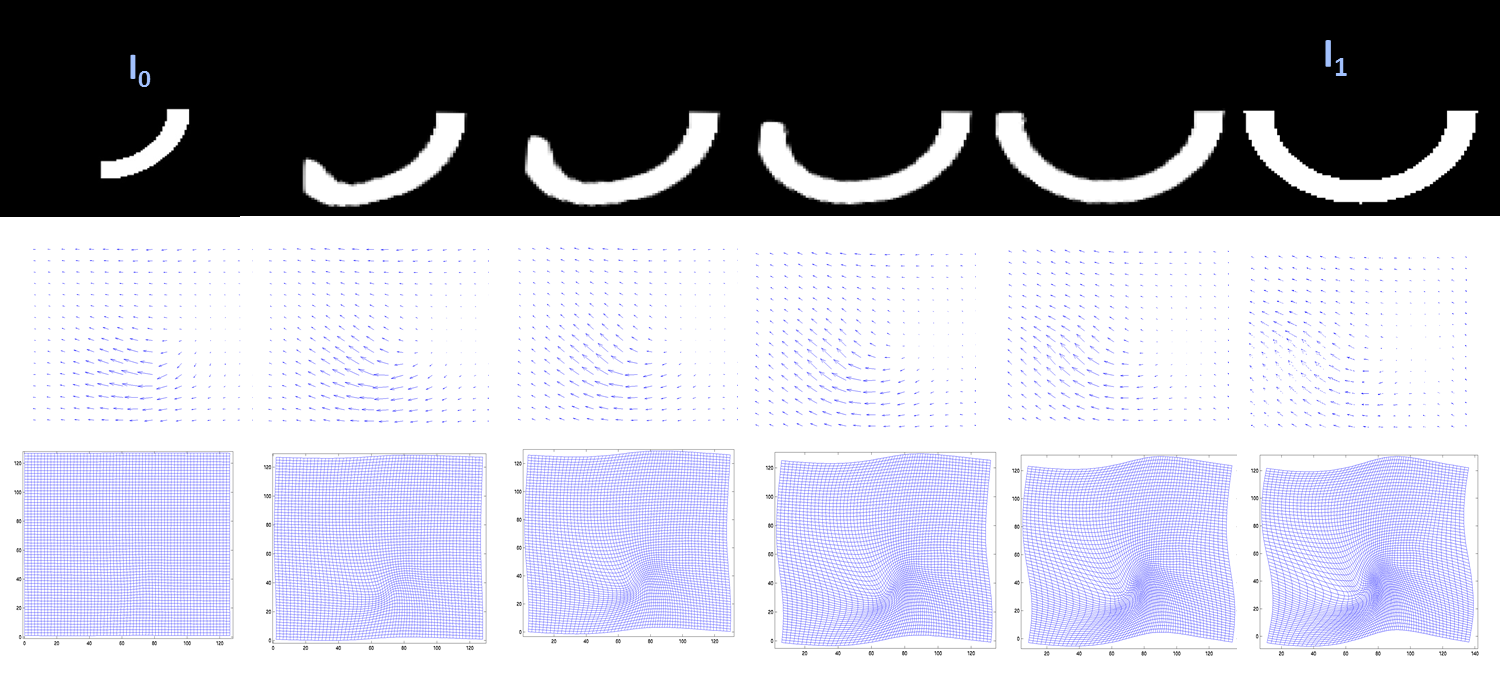
Large Deformation Diffeomorphic Metric Mapping
Large deformation diffeomorphic metric mapping (LDDMM) is a specific suite of algorithms used for diffeomorphic mapping and manipulating dense imagery based on diffeomorphic metric mapping within the academic discipline of computational anatomy, to be distinguished from its precursor based on diffeomorphic mapping. The distinction between the two is that diffeomorphic metric maps satisfy the property that the length associated to their flow away from the identity induces a metric on the group of diffeomorphisms, which in turn induces a metric on the orbit of shapes and forms within the field of Computational Anatomy. The study of shapes and forms with the metric of diffeomorphic metric mapping is called diffeomorphometry. A diffeomorphic mapping system is a system designed to map, manipulate, and transfer information which is stored in many types of spatially distributed medical imagery. Diffeomorphic mapping is the underlying technology for mapping and analyzing information m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape Analysis (other)
Shape analysis may refer to: * Shape analysis (digital geometry) * Shape analysis (program analysis), a type of method to analyze computer programs without actually executing the programs * Statistical shape analysis * Computational anatomy#Statistical shape theory in computational anatomy * Computational anatomy Computational anatomy is an interdisciplinary field of biology focused on quantitative investigation and modelling of anatomical shapes variability. It involves the development and application of mathematical, statistical and data-analytical metho ... * Bayesian Estimation of Templates in Computational Anatomy * Nucleic acid structure determination#SHAPE, a type of RNA chemical probing to produce secondary structure models {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Data Analysis
Geometric data analysis comprises geometric aspects of image analysis, pattern analysis, and shape analysis, and the approach of multivariate statistics, which treat arbitrary data sets as ''clouds of points'' in a space that is ''n''-dimensional. This includes topological data analysis, cluster analysis, inductive data analysis, correspondence analysis, multiple correspondence analysis, principal components analysis and See also * Algebraic statistics for algebraic-geometry in statistics *Combinatorial data analysis *Computational anatomy for the study of shapes and forms at the morphome scale *Structured data analysis (statistics) Structured data analysis is the statistical data analysis of structured data. This can arise either in the form of an ''a priori'' structure such as multiple-choice questionnaires or in situations with the need to search for structure that fits t ... References * * Approximation of Geodesic Distances for Geometric Data Analysis Differential geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Active Shape Model
Active shape models (ASMs) are statistical models of the shape of objects which iteratively deform to fit to an example of the object in a new image, developed by Tim Cootes and Chris Taylor in 1995. The shapes are constrained by the PDM (point distribution model) Statistical Shape Model to vary only in ways seen in a training set of labelled examples. The shape of an object is represented by a set of points (controlled by the shape model). The ASM algorithm aims to match the model to a new image. The ASM works by alternating the following steps: * Generate a suggested shape by looking in the image around each point for a better position for the point. This is commonly done using what is called a "profile model", which looks for strong edges or uses the Mahalanobis distance to match a model template for the point. * Conform the suggested shape to the point distribution model, commonly called a "shape model" in this context. The figure to the right shows an example. The techni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voxel-based Morphometry
Voxel-based morphometry is a computational approach to neuroanatomy that measures differences in local concentrations of brain tissue, through a voxel-wise comparison of multiple brain images. In traditional morphometry, volume of the whole brain or its subparts is measured by drawing regions of interest (ROIs) on images from brain scanning and calculating the volume enclosed. However, this is time consuming and can only provide measures of rather large areas. Smaller differences in volume may be overlooked. The value of VBM is that it allows for comprehensive measurement of differences, not just in specific structures, but throughout the entire brain. VBM registers every brain to a template, which gets rid of most of the large differences in brain anatomy among people. Then the brain images are smoothed so that each voxel represents the average of itself and its neighbors. Finally, the image volume is compared across brains at every voxel. However, VBM can be sensitive to vari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Large Deformation Diffeomorphic Metric Mapping
Large deformation diffeomorphic metric mapping (LDDMM) is a specific suite of algorithms used for diffeomorphic mapping and manipulating dense imagery based on diffeomorphic metric mapping within the academic discipline of computational anatomy, to be distinguished from its precursor based on diffeomorphic mapping. The distinction between the two is that diffeomorphic metric maps satisfy the property that the length associated to their flow away from the identity induces a metric on the group of diffeomorphisms, which in turn induces a metric on the orbit of shapes and forms within the field of Computational Anatomy. The study of shapes and forms with the metric of diffeomorphic metric mapping is called diffeomorphometry. A diffeomorphic mapping system is a system designed to map, manipulate, and transfer information which is stored in many types of spatially distributed medical imagery. Diffeomorphic mapping is the underlying technology for mapping and analyzing information m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Anatomy
Computational anatomy is an interdisciplinary field of biology focused on quantitative investigation and modelling of anatomical shapes variability. It involves the development and application of mathematical, statistical and data-analytical methods for modelling and simulation of biological structures. The field is broadly defined and includes foundations in anatomy, applied mathematics and pure mathematics, machine learning, computational mechanics, computational science, biological imaging, neuroscience, physics, probability, and statistics; it also has strong connections with fluid mechanics and geometric mechanics. Additionally, it complements newer, interdisciplinary fields like bioinformatics and neuroinformatics in the sense that its interpretation uses metadata derived from the original sensor imaging modalities (of which magnetic resonance imaging is one example). It focuses on the anatomical structures being imaged, rather than the medical imaging devices. It is similar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Metric Space Of Shapes And Forms
''The'' () is a grammatical article in English, denoting persons or things that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with nouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of the archaic pron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mapping (mathematics)
In mathematics, a map or mapping is a function in its general sense. These terms may have originated as from the process of making a geographical map: ''mapping'' the Earth surface to a sheet of paper. The term ''map'' may be used to distinguish some special types of functions, such as homomorphisms. For example, a linear map is a homomorphism of vector spaces, while the term linear function may have this meaning or it may mean a linear polynomial. In category theory, a map may refer to a morphism. The term ''transformation'' can be used interchangeably, but ''transformation'' often refers to a function from a set to itself. There are also a few less common uses in logic and graph theory. Maps as functions In many branches of mathematics, the term ''map'' is used to mean a function, sometimes with a specific property of particular importance to that branch. For instance, a "map" is a "continuous function" in topology, a "linear transformation" in linear algebra, etc. Some au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Force (physics)
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newton (N). Force is represented by the symbol (formerly ). The original form of Newton's second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. Concepts related to force include: thrust, which increases the velocity of an object; drag, which decreases the velocity of an object; and torque, which produces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




.png)