|
Stationary And Inflection Pts
In addition to its common meaning, stationary may have the following specialized scientific meanings: Mathematics * Stationary point * Stationary process * Stationary state Meteorology * A stationary front is a weather front that is not moving Physics * A time-invariant system quantity, such as a constant position or temperature * A steady state physical process, such as a vibration at constant amplitude and frequency or a steady fluid flow * A stationary wave is a standing wave * Stationary spacetime In general relativity, specifically in the Einstein field equations, a spacetime is said to be stationary if it admits a Killing vector that is asymptotically timelike. Description and analysis In a stationary spacetime, the metric tensor comp ... in general relativity Other uses * "Stationary", a song from ''Copacetic'' (Knuckle Puck album) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" increasing or decreasing (hence the name). For a differentiable function of several real variables, a stationary point is a point on the surface of the graph where all its partial derivatives are zero (equivalently, the gradient is zero). Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., parallel to the -axis). For a function of two variables, they correspond to the points on the graph where the tangent plane is parallel to the plane. Turning points A turning point is a point at which the derivative changes sign. A turning point may be either a relative maximum or a relative minimum (also known as local minimum and maximum). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Process
In mathematics and statistics, a stationary process (or a strict/strictly stationary process or strong/strongly stationary process) is a stochastic process whose unconditional joint probability distribution does not change when shifted in time. Consequently, parameters such as mean and variance also do not change over time. If you draw a line through the middle of a stationary process then it should be flat; it may have 'seasonal' cycles, but overall it does not trend up nor down. Since stationarity is an assumption underlying many statistical procedures used in time series analysis, non-stationary data are often transformed to become stationary. The most common cause of violation of stationarity is a trend in the mean, which can be due either to the presence of a unit root or of a deterministic trend. In the former case of a unit root, stochastic shocks have permanent effects, and the process is not mean-reverting. In the latter case of a deterministic trend, the process is called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary State
A stationary state is a quantum state with all observables independent of time. It is an eigenvector of the energy operator (instead of a quantum superposition of different energies). It is also called energy eigenvector, energy eigenstate, energy eigenfunction, or energy eigenket. It is very similar to the concept of atomic orbital and molecular orbital in chemistry, with some slight differences explained below. Introduction A stationary state is called ''stationary'' because the system remains in the same state as time elapses, in every observable way. For a single-particle Hamiltonian, this means that the particle has a constant probability distribution for its position, its velocity, its spin, etc. (This is true assuming the particle's environment is also static, i.e. the Hamiltonian is unchanging in time.) The wavefunction itself is not stationary: It continually changes its overall complex phase factor, so as to form a standing wave. The oscillation frequency of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Front
A stationary front (or quasi-stationary front) is a weather front or transition zone between two air masses when both air mass is advancing into the other at speeds exceeding 5 knots (about 6 miles per hour or about 9 kilometers per hour) at the ground surface. On weather maps, it's illustrated as a solid line of alternating blue spikes pointing to the warmer air mass and red domes facing the colder air mass. Development A stationary front may form when a cold or warm front slows down or grows over time from underlying surface temperature differences, like a coastal front. Winds on the cold air and warm air sides often flow nearly parallel to the stationary front, often in opposite directions along either side of the stationary front. A stationary front usually remains in the same area for hours to days and may undulate as atmospheric waves move eastward along the front. Stationary fronts may also change into a cold or warm front and may form one or more extratropical or mid-latit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-invariant System
In control theory, a time-invariant (TIV) system has a time-dependent system function that is not a direct function of time. Such systems are regarded as a class of systems in the field of system analysis. The time-dependent system function is a function of the time-dependent input function. If this function depends ''only'' indirectly on the time-domain (via the input function, for example), then that is a system that would be considered time-invariant. Conversely, any direct dependence on the time-domain of the system function could be considered as a "time-varying system". Mathematically speaking, "time-invariance" of a system is the following property: :''Given a system with a time-dependent output function , and a time-dependent input function , the system will be considered time-invariant if a time-delay on the input directly equates to a time-delay of the output function. For example, if time is "elapsed time", then "time-invariance" implies that the relationship betw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steady State
In systems theory, a system or a Process theory, process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p'' of the system, the partial derivative with respect to time is zero and remains so: : \frac = 0 \quad \text t. In discrete time, it means that the first difference of each property is zero and remains so: :p_t-p_=0 \quad \text t. The concept of a steady state has relevance in many fields, in particular thermodynamics, Steady state economy, economics, and engineering. If a system is in a steady state, then the recently observed behavior of the system will continue into the future. In stochastic systems, the probabilities that various states will be repeated will remain constant. See for example Linear difference equation#Conversion to homogeneous form for the derivation of the steady state. In many systems, a steady state i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
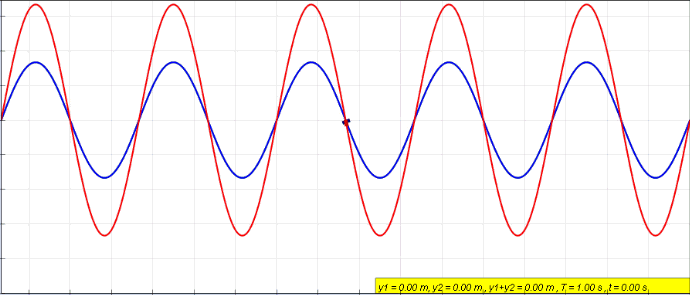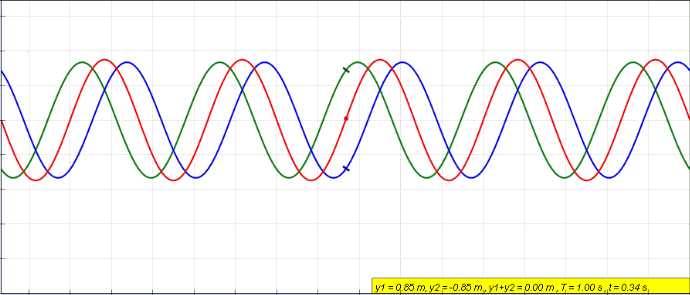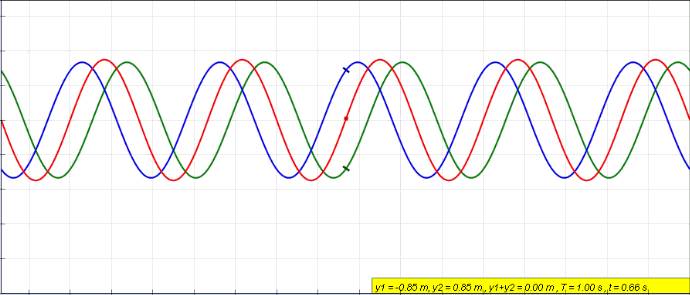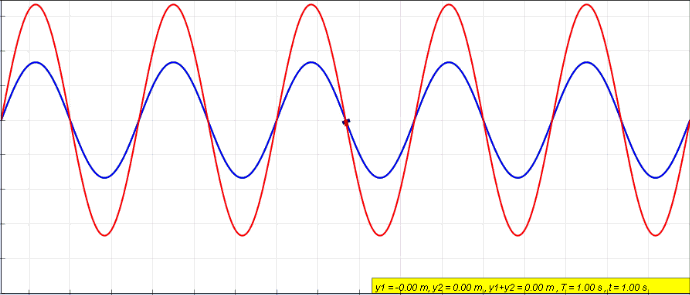
Standing Wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes. Standing waves were first noticed by Michael Faraday in 1831. Faraday observed standing waves on the surface of a liquid in a vibrating container. Franz Melde coined the term "standing wave" (German: ''stehende Welle'' or ''Stehwelle'') around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings. This phenomenon can occur because the medium is moving in the direction opposite to the movement of the wave, or it can arise in a stationary medium ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Spacetime
In general relativity, specifically in the Einstein field equations, a spacetime is said to be stationary if it admits a Killing vector that is asymptotically timelike. Description and analysis In a stationary spacetime, the metric tensor components, g_, may be chosen so that they are all independent of the time coordinate. The line element of a stationary spacetime has the form (i,j = 1,2,3) : ds^ = \lambda (dt - \omega_\, dy^i)^ - \lambda^ h_\, dy^i\,dy^j, where t is the time coordinate, y^ are the three spatial coordinates and h_ is the metric tensor of 3-dimensional space. In this coordinate system the Killing vector field \xi^ has the components \xi^ = (1,0,0,0). \lambda is a positive scalar representing the norm of the Killing vector, i.e., \lambda = g_\xi^\xi^, and \omega_ is a 3-vector, called the twist vector, which vanishes when the Killing vector is hypersurface orthogonal. The latter arises as the spatial components of the twist 4-vector \omega_ = e_\xi^\nabla^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |