|
Star-shaped Preferences
In social choice theory, star-shaped preferences are a class of preferences over points in a Euclidean space. An agent with star-shaped preferences has a unique ideal point (optimum), where he is maximally satisfied. Moreover, he becomes less and less satisfied as the actual distribution moves away from his optimum. Star-shaped preferences can be seen as a multi-dimensional extension of single-peaked preferences. Background Often, society has to choose a point from a subset of a Euclidean space. For example, society has to choose how to distribute its annual budget; each potential distribution is a vector of real numbers. If there are ''m'' potential issues in the budget, then the set of all potential budget distributions is a subset of R''m'' - the m-dimensional Euclidean space. Different members of society may have different preferences over budget distributions. A ''preference'' is any total order over points. For example, a particular agent may state that he prefers the distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Choice Theory
Social choice theory is a branch of welfare economics that extends the Decision theory, theory of rational choice to collective decision-making. Social choice studies the behavior of different mathematical procedures (social welfare function, social welfare functions) used to combine individual preferences into a coherent whole.Amartya Sen (2008). "Social Choice". ''The New Palgrave Dictionary of Economics'', 2nd EditionAbstract & TOC./ref> It contrasts with political science in that it is a Normative economics, normative field that studies how a society can make good decisions, whereas political science is a Positive economics, descriptive field that observes how societies actually do make decisions. While social choice began as a branch of economics and decision theory, it has since received substantial contributions from mathematics, philosophy, political science, and game theory. Real-world examples of social choice rules include constitution, constitutions and Parliamentary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preference (economics)
In economics, and in other social sciences, preference refers to an order by which an Agent (economics), agent, while in search of an "optimal choice", ranks alternatives based on their respective utility. ''Preferences'' are evaluations that concern matters of value, in relation to practical reasoning. Individual preferences are determined by taste, need, ..., as opposed to price, availability or personal income. Classical economics assumes that people act in their best (rational) interest. In this context, rationality would dictate that, when given a choice, an individual will select an option that maximizes their self-interest. But preferences are not always transitive relation, transitive, both because real humans are far from always being rational and because in some situations preferences can form cycle (graph theory), cycles, in which case there exists no well-defined optimal choice. An example of this is Efron dice. The concept of preference plays a key role in many discip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
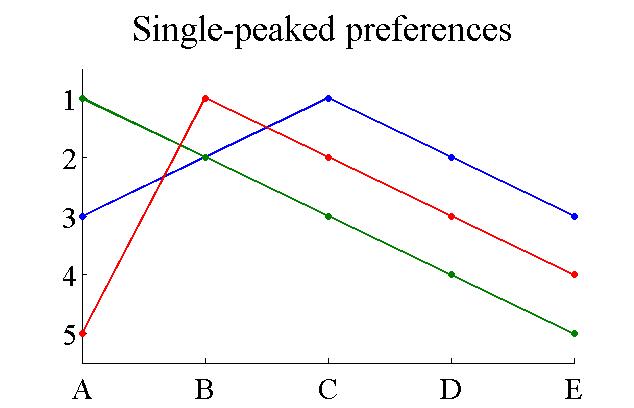
Single-peaked Preferences
Single-peaked preferences are a class of preference relations. A group has single-peaked preferences over a set of outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome, which is to select the median quantity; this results in the median voter theorem. It is truthful because the median function satisfies the strong monotonicity property. The notion wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Order
In mathematics, a total order or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation \leq on some set X, which satisfies the following for all a, b and c in X: # a \leq a ( reflexive). # If a \leq b and b \leq c then a \leq c ( transitive). # If a \leq b and b \leq a then a = b ( antisymmetric). # a \leq b or b \leq a ( strongly connected, formerly called totality). Requirements 1. to 3. just make up the definition of a partial order. Reflexivity (1.) already follows from strong connectedness (4.), but is required explicitly by many authors nevertheless, to indicate the kinship to partial orders. Total orders are sometimes also called simple, connex, or full orders. A set equipped with a total order is a totally ordered set; the terms simply ordered set, linearly ordered set, toset and loset are also used. The term ''chain'' is sometimes defined as a synonym of ''totally ordered set'', but generally refers to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-peaked Preferences
Single-peaked preferences are a class of preference relations. A group has single-peaked preferences over a set of outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome, which is to select the median quantity; this results in the median voter theorem. It is truthful because the median function satisfies the strong monotonicity property. The notion wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utility
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings. * In a normative context, utility refers to a goal or objective that we wish to maximize, i.e., an objective function. This kind of utility bears a closer resemblance to the original utilitarian concept, developed by moral philosophers such as Jeremy Bentham and John Stuart Mill. * In a descriptive context, the term refers to an ''apparent'' objective function; such a function is revealed by a person's behavior, and specifically by their preferences over lotteries, which can be any quantified choice. The relationship between these two kinds of utility functions has been a source of controversy among both economists and ethicists, with most maintaining that the two are distinct but generally related. Utility function Consider a set of alternatives among which a person has a preference ordering. A utility fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. It has unique properties, for example when the identity matrix represents a geometric transformation, the object remains unchanged by the transformation. In other contexts, it is analogous to multiplying by the number 1. Terminology and notation The identity matrix is often denoted by I_n, or simply by I if the size is immaterial or can be trivially determined by the context. I_1 = \begin 1 \end ,\ I_2 = \begin 1 & 0 \\ 0 & 1 \end ,\ I_3 = \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end ,\ \dots ,\ I_n = \begin 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end. The term unit matrix has also been widely used, but the term ''identity matrix'' is now standard. The term ''unit matrix'' is ambiguous, because it is also used for a matrix of on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras. In the Greek deductive geometry exemplified by Euclid's ''Elements'', distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass tool used to draw a circle, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Insurance
Insurance is a means of protection from financial loss in which, in exchange for a fee, a party agrees to compensate another party in the event of a certain loss, damage, or injury. It is a form of risk management, primarily used to protect against the risk of a contingent or uncertain loss. An entity which provides insurance is known as an insurer, insurance company, insurance carrier, or underwriter. A person or entity who buys insurance is known as a policyholder, while a person or entity covered under the policy is called an insured. The insurance transaction involves the policyholder assuming a guaranteed, known, and relatively small loss in the form of a payment to the insurer (a premium) in exchange for the insurer's promise to compensate the insured in the event of a covered loss. The loss may or may not be financial, but it must be reducible to financial terms. Furthermore, it usually involves something in which the insured has an insurable interest established by o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lottery
A lottery (or lotto) is a form of gambling that involves the drawing of numbers at random for a prize. Some governments outlaw lotteries, while others endorse it to the extent of organizing a national or state lottery. It is common to find some degree of regulation of lottery by governments. The most common regulations are prohibition of sale to minors and licensing of ticket vendors. Although lotteries were common in the United States and some other countries during the 19th century, by the beginning of the 20th century, most forms of gambling, including lotteries and sweepstakes, were illegal in the U.S. and most of Europe as well as many other countries. This remained so until well after World War II. In the 1960s, casinos and lotteries began to re-appear throughout the world as a means for governments to raise revenue without raising taxes. Lotteries come in many formats. For example, the prize can be a fixed amount of cash or goods. In this format, there is risk to the org ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preference Classes Venn Diagram
In psychology, economics and philosophy, preference is a technical term usually used in relation to choosing between alternatives. For example, someone prefers A over B if they would rather choose A than B. Preferences are central to decision theory because of this relation to behavior. Some methods such as Ordinal Priority Approach use preference relation for decision-making. As connative states, they are closely related to desires. The difference between the two is that desires are directed at one object while preferences concern a comparison between two alternatives, of which one is preferred to the other. In insolvency, the term is used to determine which outstanding obligation the insolvent party has to settle first. Psychology In psychology, preferences refer to an individual's attitude towards a set of objects, typically reflected in an explicit decision-making process. The term is also used to mean evaluative judgment in the sense of liking or disliking an object, as in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |