|
Spike-triggered Average
The spike-triggered averaging (STA) is a tool for characterizing the response properties of a neuron using the spikes emitted in response to a time-varying stimulus. The STA provides an estimate of a neuron's linear receptive field. It is a useful technique for the analysis of electrophysiological data. Mathematically, the STA is the average stimulus preceding a spike.de Boer and Kuyper (1968) Triggered Correlation. ''IEEE Transact. Biomed. Eng.'', 15:169-179Marmarelis, P. Z. and Naka, K. (1972). White-noise analysis of a neuron chain: an application of the Wiener theory. ''Science'', 175:1276-1278Chichilnisky, E. J. (2001). A simple white noise analysis of neuronal light responses. ''Network: Computation in Neural Systems'', 12:199-213Simoncelli, E. P., Paninski, L., Pillow, J. & Swartz, O. (2004)."Characterization of neural responses with stochastic stimuli" In M. Gazzaniga (Ed.) ''The Cognitive Neurosciences, III'' (pp. 327-338). MIT press. To compute the STA, the stimulus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
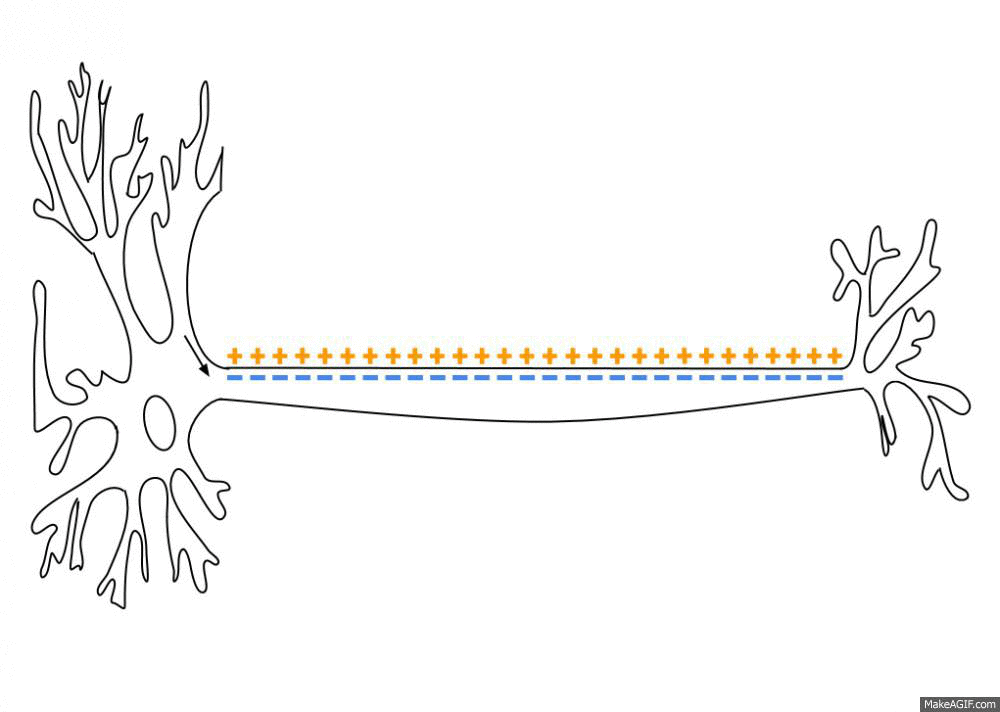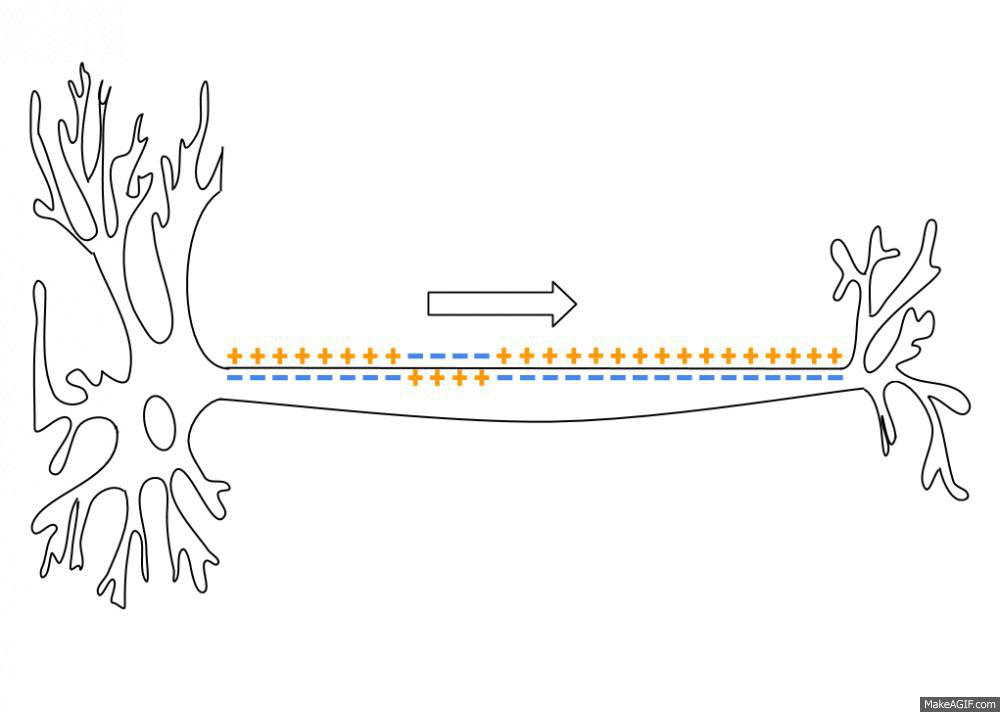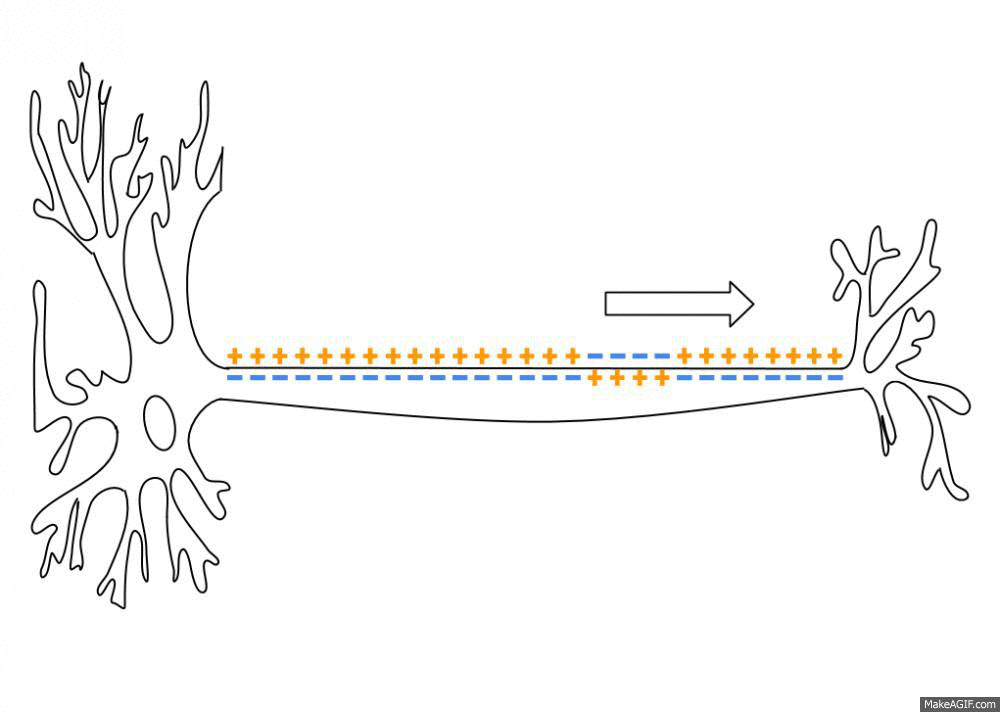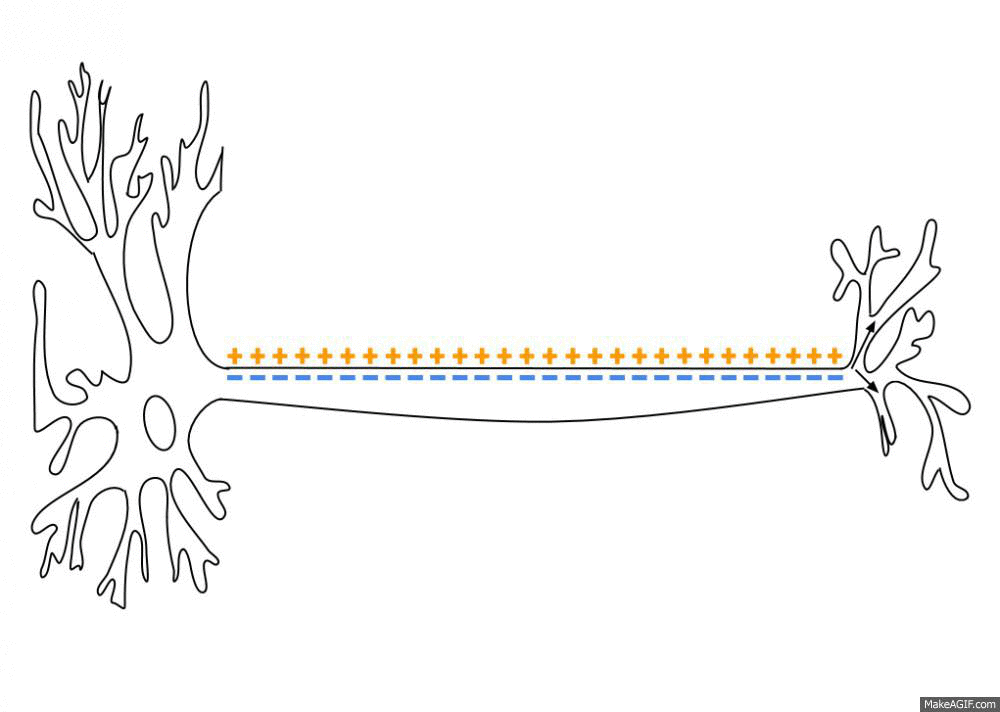
Action Potentials
An action potential occurs when the membrane potential of a specific cell location rapidly rises and falls. This depolarization then causes adjacent locations to similarly depolarize. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and in some plant cells. Certain endocrine cells such as pancreatic beta cells, and certain cells of the anterior pituitary gland are also excitable cells. In neurons, action potentials play a central role in cell-cell communication by providing for—or with regard to saltatory conduction, assisting—the propagation of signals along the neuron's axon toward synaptic boutons situated at the ends of an axon; these signals can then connect with other neurons at synapses, or to motor cells or glands. In other types of cells, their main function is to activate intracellular processes. In muscle cells, for example, an action potential is the first step in the chain of event ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tikhonov Regularization
Ridge regression is a method of estimating the coefficients of multiple- regression models in scenarios where the independent variables are highly correlated. It has been used in many fields including econometrics, chemistry, and engineering. Also known as Tikhonov regularization, named for Andrey Tikhonov, it is a method of regularization of ill-posed problems. It is particularly useful to mitigate the problem of multicollinearity in linear regression, which commonly occurs in models with large numbers of parameters. In general, the method provides improved efficiency in parameter estimation problems in exchange for a tolerable amount of bias (see bias–variance tradeoff). The theory was first introduced by Hoerl and Kennard in 1970 in their '' Technometrics'' papers “RIDGE regressions: biased estimation of nonorthogonal problems” and “RIDGE regressions: applications in nonorthogonal problems”. This was the result of ten years of research into the field of ridge a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sliced Inverse Regression
Sliced inverse regression (or SIR) is a tool for dimensionality reduction in the field of multivariate statistics. In statistics, regression analysis is a method of studying the relationship between a response variable ''y'' and its input variable \underline, which is a ''p''-dimensional vector. There are several approaches in the category of regression. For example, parametric methods include multiple linear regression, and non-parametric methods include local smoothing. As the number of observations needed to use local smoothing methods scales exponentially with high-dimensional data (as ''p'' grows), reducing the number of dimensions can make the operation computable. Dimensionality reduction aims to achieve this by showing only the most important dimension of the data. SIR uses the inverse regression curve, E(\underline\,, \,y), to perform a weighted principal component analysis. Model Given a response variable \,Y and a (random) vector X \in \R^p of explanatory variables, S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spike-triggered Covariance
Spike-triggered covariance (STC) analysis is a tool for characterizing a neuron's response properties using the covariance of stimuli that elicit spikes from a neuron. STC is related to the spike-triggered average (STA), and provides a complementary tool for estimating linear filters in a linear-nonlinear-Poisson (LNP) cascade model. Unlike STA, the STC can be used to identify a multi-dimensional feature space in which a neuron computes its response. STC analysis identifies the stimulus features affecting a neuron's response via an eigenvector decomposition of the spike-triggered covariance matrix.Brenner, N., Bialek, W., & de Ruyter van Steveninck, R.R. (2000). Schwartz, O., Chichilnisky, E. J., & Simoncelli, E. P. (2002). Bialek, W. & de Ruyter van Steveninck, R. (2005). Arxiv preprint q-bio/0505003.Schwartz O., Pillow J. W., Rust N. C., & Simoncelli E. P. (2006). Spike-triggered neural characterization. ''Journal of Vision'' 6:484-507 Eigenvectors with eigenvalues significant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the " amount of information" (in units such as shannons (bits), nats or hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and Y. MI is the expected value of the pointwise mutual information (PMI). The quantity was defined and analyzed by Claude Shannon in his landmark paper " A Mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Likelihood
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference. If the likelihood function is differentiable, the derivative test for finding maxima can be applied. In some cases, the first-order conditions of the likelihood function can be solved analytically; for instance, the ordinary least squares estimator for a linear regression model maximizes the likelihood when all observed outcomes are assumed to have Normal distributions with the same variance. From the perspective of Bayesian in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Efficient Estimator
In statistics, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator, needs fewer input data or observations than a less efficient one to achieve the Cramér–Rao bound. An ''efficient estimator'' is characterized by having the smallest possible variance, indicating that there is a small deviance between the estimated value and the "true" value in the L2 norm sense. The relative efficiency of two procedures is the ratio of their efficiencies, although often this concept is used where the comparison is made between a given procedure and a notional "best possible" procedure. The efficiencies and the relative efficiency of two procedures theoretically depend on the sample size available for the given procedure, but it is often possible to use the asymptotic relative efficiency (defined as the limit of the relative efficiencies as the sample size grows) as the principal com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bussgang Theorem
In mathematics, the Bussgang theorem is a theorem of stochastic analysis. The theorem states that the cross-correlation of a Gaussian signal before and after it has passed through a nonlinear operation are equal up to a constant. It was first published by Julian J. Bussgang in 1952 while he was at the Massachusetts Institute of Technology.J.J. Bussgang,"Cross-correlation function of amplitude-distorted Gaussian signals", Res. Lab. Elec., Mas. Inst. Technol., Cambridge MA, Tech. Rep. 216, March 1952. Statement Let \left\ be a zero-mean stationary Gaussian random process and \left \ = g(X(t)) where g(\cdot) is a nonlinear amplitude distortion. If R_X(\tau) is the autocorrelation function of \left\, then the cross-correlation function In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptical Distribution
In probability and statistics, an elliptical distribution is any member of a broad family of probability distributions that generalize the multivariate normal distribution. Intuitively, in the simplified two and three dimensional case, the joint distribution forms an ellipse and an ellipsoid, respectively, in iso-density plots. In statistics, the normal distribution is used in ''classical'' multivariate analysis, while elliptical distributions are used in ''generalized'' multivariate analysis, for the study of symmetric distributions with tails that are heavy, like the multivariate t-distribution, or light (in comparison with the normal distribution). Some statistical methods that were originally motivated by the study of the normal distribution have good performance for general elliptical distributions (with finite variance), particularly for spherical distributions (which are defined below). Elliptical distributions are also used in robust statistics to evaluate proposed multiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consistent Estimator
In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter ''θ''0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to ''θ''0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to ''θ''0 converges to one. In practice one constructs an estimator as a function of an available sample of size ''n'', and then imagines being able to keep collecting data and expanding the sample ''ad infinitum''. In this way one would obtain a sequence of estimates indexed by ''n'', and consistency is a property of what occurs as the sample size “grows to infinity”. If the sequence of estimates can be mathematically shown to converge in probability to the true value ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |