|
Sphenomegacorona
In geometry, the sphenomegacorona is a Johnson solid with 16 equilateral triangles and 2 squares as its faces. Properties The sphenomegacorona was named by in which he used the prefix ''spheno-'' referring to a wedge-like complex formed by two adjacent ''lunes''—a square with equilateral triangles attached on its opposite sides. The suffix ''-megacorona'' refers to a crownlike complex of 12 triangles, contrasted with the smaller triangular complex that makes the sphenocorona. By joining both complexes, the resulting polyhedron has 16 equilateral triangles and 2 squares, making 18 faces. All of its faces are regular polygons, categorizing the sphenomegacorona as a Johnson solid—a convex polyhedron in which all of the faces are regular polygons—enumerated as the 88th Johnson solid J_ . It is an elementary polyhedron, meaning it cannot be separated by a plane into two small regular-faced polyhedra. The surface area of a sphenomegacorona A is the total of p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hebesphenomegacorona
In geometry, the hebesphenomegacorona is a Johnson solid with 18 equilateral triangles and 3 squares as its faces. Properties The hebesphenomegacorona is named by in which he used the prefix ''hebespheno-'' referring to a blunt wedge-like complex formed by three adjacent ''lunes''—a square with equilateral triangles attached on its opposite sides. The suffix ''-megacorona'' refers to a crownlike complex of 12 triangles. By joining both complexes together, the result polyhedron has 18 equilateral triangles and 3 squares, making 21 faces.. All of its faces are regular polygons, categorizing the hebesphenomegacorona as a Johnson solid—a convex polyhedron in which all of its faces are regular polygons—enumerated as 89th Johnson solid J_ . It is an elementary polyhedron, meaning it cannot be separated by a plane into two small regular-faced polyhedra. The surface area of a hebesphenomegacorona with edge length a can be determined by adding the area of its fac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, solids with such a property: the first solids are the Pyramid (geometry), pyramids, Cupola (geometry), cupolas, and a Rotunda (geometry), rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many Half-space (geometry), half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not Uniform polyhedron, uniform. This means that a Johnson solid is not a Platonic solid, Arc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
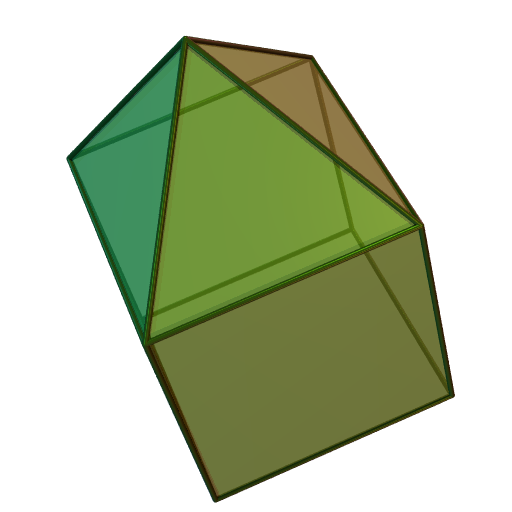
Augmented Sphenocorona
In geometry, the augmented sphenocorona is the Johnson solid that can be constructed by attaching an equilateral square pyramid to one of the square faces of the sphenocorona. It is the only Johnson solid arising from "cut and paste" manipulations where the components are not all prisms, antiprisms or sections of Platonic solid, Platonic or Archimedean solid, Archimedean solids. Construction The augmented sphenocorona is constructed by attaching equilateral square pyramid to the sphenocorona, a process known as the Augmentation (geometry), augmentation. This pyramid covers one square face of the sphenocorona, replacing them with equilateral triangles. As a result, the augmented sphenocorona has 16 equilateral triangles and 1 square as its faces. The convex polyhedron with its Regular polygon, faces are regular is the Johnson solid; the augmented sphenocorona is one of them, enumerated as J_ , the 87th Johnson solid. Properties For the edge length a , the surface area of an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object ''X'' is ''G'' = Sym(''X''). For an object in a metric space, its symmetries form a subgroup of the isometry group of the ambient space. This article mainly considers symmetry groups in Euclidean geometry, but the concept may also be studied for more general types of geometric structure. Introduction We consider the "objects" possessing symmetry to be geometric figures, images, and patterns, such as a wallpaper pattern. For symmetry of physical objects, one may also take their physical composition as part of the pattern. (A pattern may be specified formally as a scalar field, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problem (mathematics education), word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Polyhedron
In geometry, a composite polyhedron is a convex polyhedron that produces other polyhedrons when sliced by a plane. Examples can be found in Johnson solids. Definition and examples A convex polyhedron is said to be ''composite'' if there exists a plane through a cycle of its edges that is not a face. Slicing the polyhedron on this plane produces two polyhedra, having together the same faces as the original polyhedron along with two new faces on the plane of the slice. Repeated slicing of this type decomposes any polyhedron into non-composite or ''elementary'' polyhedra. Some examples of non-composite polyhedron are the prisms, antiprisms, and the other seventeen Johnson solids. Among the regular polyhedra, the regular octahedron and regular icosahedron are composite. Any composite polyhedron can be constructed by attaching two or more non-composite polyhedra. Alternatively, it can be defined as a convex polyhedron that can separated into two or more non-composite polyhedra. Exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a set of points is convex if it contains every line segment between two points in the set. For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary (topology), boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval (mathematics), interval with the property that its epigraph (mathematics), epigraph (the set of points on or above the graph of a function, graph of the function) is a convex set. Convex minimization is a subfield of mathematical optimization, optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphenocorona
In geometry, the sphenocorona is a Johnson solid with 12 equilateral triangles and 2 squares as its faces. Properties The sphenocorona was named by in which he used the prefix ''spheno-'' referring to a wedge-like complex formed by two adjacent '' lunes''—a square with equilateral triangles attached on its opposite sides. The suffix ''-corona'' refers to a crownlike complex of 8 equilateral triangles. By joining both complexes together, the resulting polyhedron has 12 equilateral triangles and 2 squares, making 14 faces. A convex polyhedron in which all faces are regular polygons is called a Johnson solid. The sphenocorona is among them, enumerated as the 86th Johnson solid J_ . It is an elementary polyhedron, meaning it cannot be separated by a plane into two small regular-faced polyhedra. The surface area of a sphenocorona with edge length a can be calculated as: A=\left(2+3\sqrt\right)a^2\approx7.19615a^2, and its volume as: \left(\frac\sqrt\right)a^3\approx1.51 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |