|
Spectral Submanifold
In dynamical systems, a spectral submanifold (SSM) is the unique smoothest invariant manifold serving as the nonlinear extension of a spectral subspace of a linear dynamical system under the addition of nonlinearities. SSM theory provides conditions for when invariant properties of eigenspaces of a linear dynamical system can be extended to a nonlinear system, and therefore motivates the use of SSMs in nonlinear dimensionality reduction. Definition Consider a nonlinear ordinary differential equation of the form :\frac = Ax + f_0(x),\quad x\in \R^n, with constant matrix \ A\in \R^ and the nonlinearities contained in the smooth function f_0 = \mathcal(, x, ^2). Assume that \text \lambda_j 0. Existence The spectral submanifold tangent to E at the origin is guaranteed to exist provided that certain non-resonance conditions are satisfied by the eigenvalues \lambda^E_i in the spectrum of E. In particular, there can be no linear combination of \lambda^E_i equal to one of the eigenva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Submanifold
In dynamical systems, a spectral submanifold (SSM) is the unique smoothest invariant manifold serving as the nonlinear extension of a spectral subspace of a linear dynamical system under the addition of nonlinearities. SSM theory provides conditions for when invariant properties of eigenspaces of a linear dynamical system can be extended to a nonlinear system, and therefore motivates the use of SSMs in nonlinear dimensionality reduction. Definition Consider a nonlinear ordinary differential equation of the form :\frac = Ax + f_0(x),\quad x\in \R^n, with constant matrix \ A\in \R^ and the nonlinearities contained in the smooth function f_0 = \mathcal(, x, ^2). Assume that \text \lambda_j 0. Existence The spectral submanifold tangent to E at the origin is guaranteed to exist provided that certain non-resonance conditions are satisfied by the eigenvalues \lambda^E_i in the spectrum of E. In particular, there can be no linear combination of \lambda^E_i equal to one of the eigenva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, a dynamical system has a State ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Manifold
In dynamical systems, a branch of mathematics, an invariant manifold is a topological manifold that is invariant under the action of the dynamical system. Examples include the slow manifold, center manifold, stable manifold, stable manifold, unstable manifold, subcenter manifold and inertial manifold. Typically, although by no means always, invariant manifolds are constructed as a 'perturbation' of an invariant subspace about an equilibrium. In dissipative systems, an invariant manifold based upon the gravest, longest lasting modes forms an effective low-dimensional, reduced, model of the dynamics. Definition Consider the differential equation dx/dt = f(x),\ x \in \mathbb R^n, with flow x(t)=\phi_t(x_0) being the solution of the differential equation with x(0)=x_0. A set S \subset \mathbb R^n is called an ''invariant set'' for the differential equation if, for each x_0 \in S, the solution t \mapsto \phi_t(x_0), defined on its maximal interval of existence, has its image in S. Alt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Dimensionality Reduction
Nonlinear dimensionality reduction, also known as manifold learning, refers to various related techniques that aim to project high-dimensional data onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping (either from the high-dimensional space to the low-dimensional embedding or vice versa) itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis. Applications of NLDR Consider a dataset represented as a matrix (or a database table), such that each row represents a set of attributes (or features or dimensions) that describe a particular instance of something. If the number of attributes is large, then the space of unique possible rows is exponentially large. Thus, the larger the dimensionality, the more difficult it becomes to sample the space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathematics are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvector
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-autonomous System (mathematics)
In mathematics, an autonomous system is a dynamic equation on a smooth manifold. A non-autonomous system is a dynamic equation on a smooth fiber bundle Q\to \mathbb R over \mathbb R. For instance, this is the case of non-autonomous mechanics. An ''r''-order differential equation on a fiber bundle Q\to \mathbb R is represented by a closed subbundle of a jet bundle J^rQ of Q\to \mathbb R. A dynamic equation on Q\to \mathbb R is a differential equation which is algebraically solved for a higher-order derivatives. In particular, a first-order dynamic equation on a fiber bundle Q\to \mathbb R is a kernel of the covariant differential of some connection \Gamma on Q\to \mathbb R. Given bundle coordinates (t,q^i) on Q and the adapted coordinates (t,q^i,q^i_t) on a first-order jet manifold J^1Q, a first-order dynamic equation reads : q^i_t=\Gamma (t,q^i). For instance, this is the case of Hamiltonian non-autonomous mechanics. A second-order dynamic equation : q^i_=\xi^i(t,q^j,q^j_t) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiperiodic Motion
In mathematics and theoretical physics, quasiperiodic motion is in rough terms the type of motion executed by a dynamical system containing a finite number (two or more) of incommensurable frequencies. That is, if we imagine that the phase space is modelled by a torus ''T'' (that is, the variables are periodic like angles), the trajectory of the system is modelled by a curve on ''T'' that wraps around the torus without ever exactly coming back on itself. A quasiperiodic function on the real line is the type of function (continuous, say) obtained from a function on ''T'', by means of a curve :''R'' → ''T'' which is linear (when lifted from ''T'' to its covering Euclidean space), by composition. It is therefore oscillating, with a finite number of underlying frequencies. (NB the sense in which theta functions and the Weierstrass zeta function in complex analysis are said to have quasi-periods with respect to a period lattice is something distinct from this.) The theory of alm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Manifold
In dynamical systems, a branch of mathematics, an invariant manifold is a topological manifold that is invariant under the action of the dynamical system. Examples include the slow manifold, center manifold, stable manifold, stable manifold, unstable manifold, subcenter manifold and inertial manifold. Typically, although by no means always, invariant manifolds are constructed as a 'perturbation' of an invariant subspace about an equilibrium. In dissipative systems, an invariant manifold based upon the gravest, longest lasting modes forms an effective low-dimensional, reduced, model of the dynamics. Definition Consider the differential equation dx/dt = f(x),\ x \in \mathbb R^n, with flow x(t)=\phi_t(x_0) being the solution of the differential equation with x(0)=x_0. A set S \subset \mathbb R^n is called an ''invariant set'' for the differential equation if, for each x_0 \in S, the solution t \mapsto \phi_t(x_0), defined on its maximal interval of existence, has its image in S. Alt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Dimensionality Reduction
Nonlinear dimensionality reduction, also known as manifold learning, refers to various related techniques that aim to project high-dimensional data onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping (either from the high-dimensional space to the low-dimensional embedding or vice versa) itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis. Applications of NLDR Consider a dataset represented as a matrix (or a database table), such that each row represents a set of attributes (or features or dimensions) that describe a particular instance of something. If the number of attributes is large, then the space of unique possible rows is exponentially large. Thus, the larger the dimensionality, the more difficult it becomes to sample the space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
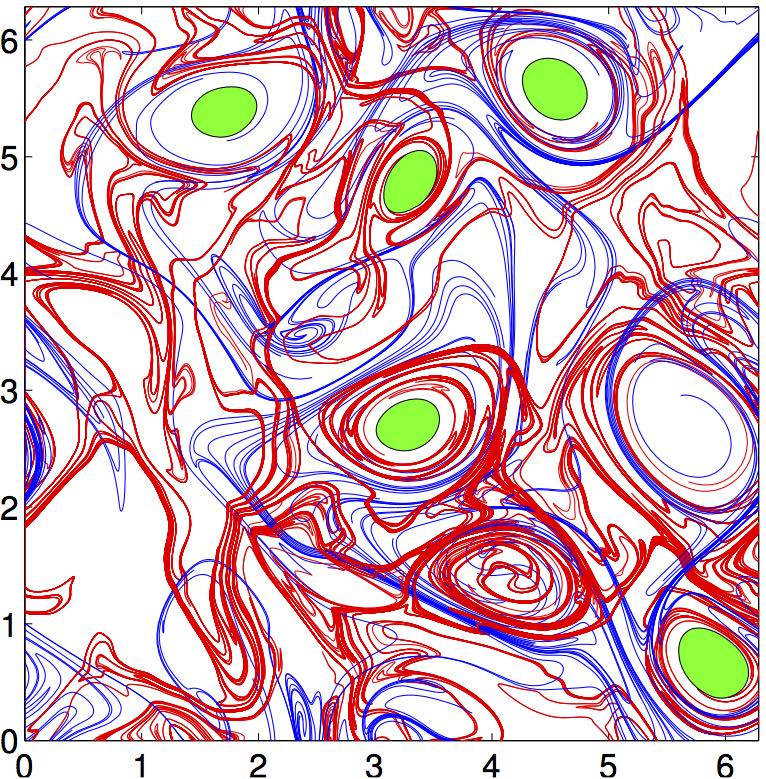
Lagrangian Coherent Structure
Lagrangian coherent structures (LCSs) are distinguished surfaces of trajectories in a dynamical system that exert a major influence on nearby trajectories over a time interval of interest. The type of this influence may vary, but it invariably creates a coherent trajectory pattern for which the underlying LCS serves as a theoretical centerpiece. In observations of tracer patterns in nature, one readily identifies coherent features, but it is often the underlying structure creating these features that is of interest. As illustrated on the right, individual tracer trajectories forming coherent patterns are generally sensitive with respect to changes in their initial conditions and the system parameters. In contrast, the LCSs creating these trajectory patterns turn out to be robust and provide a simplified skeleton of the overall dynamics of the system. The robustness of this skeleton makes LCSs ideal tools for model validation, model comparison and benchmarking. LCSs can also be use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
