|
Solar Azimuth Angle
The solar azimuth angle is the azimuth (horizontal angle with respect to north) of the Sun's position. This horizontal coordinate defines the Sun's relative direction along the local horizon, whereas the solar zenith angle (or its complementary angle solar elevation) defines the Sun's apparent altitude. Conventional sign and origin There are several conventions for the solar azimuth; however, it is traditionally defined as the angle between a line due south and the shadow cast by a vertical rod on Earth. This convention states the angle is positive if the shadow is east of south and negative if it is west of south. For example, due east would be 90° and due west would be -90°. Another convention is the reverse; it also has the origin at due south, but measures angles clockwise, so that due east is now negative and west now positive. However, despite tradition, the most commonly accepted convention for analyzing solar irradiation, e.g. for solar energy applications, is clockw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Azimuth
An azimuth (; from ar, اَلسُّمُوت, as-sumūt, the directions) is an angular measurement in a spherical coordinate system. More specifically, it is the horizontal angle from a cardinal direction, most commonly north. Mathematically, the relative position vector from an observer (origin) to a point of interest is projected perpendicularly onto a reference plane (the horizontal plane); the angle between the projected vector and a reference vector on the reference plane is called the azimuth. When used as a celestial coordinate, the azimuth is the horizontal direction of a star or other astronomical object in the sky. The star is the point of interest, the reference plane is the local area (e.g. a circular area with a 5 km radius at sea level) around an observer on Earth's surface, and the reference vector points to true north. The azimuth is the angle between the north vector and the star's vector on the horizontal plane. Azimuth is usually measured in d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formulas
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship between given quantities. The plural of ''formula'' can be either ''formulas'' (from the most common English plural noun form) or, under the influence of scientific Latin, ''formulae'' (from the original Latin). In mathematics In mathematics, a formula generally refers to an identity which equates one mathematical expression to another, with the most important ones being mathematical theorems. Syntactically, a formula (often referred to as a ''well-formed formula'') is an entity which is constructed using the symbols and formation rules of a given logical language. For example, determining the volume of a sphere requires a significant amount of integral calculus or its geometrical analogue, the method of exhaustion. However, having done th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subsolar Point
The subsolar point on a planet is the point at which its sun is perceived to be directly overhead (at the zenith); that is, where the sun's rays strike the planet exactly perpendicular to its surface. It can also mean the point closest to the sun on an astronomical object, even though the sun might not be visible. To an observer on a planet with an orientation and rotation similar to those of Earth, the subsolar point will appear to move westward, completing one circuit around the globe each day, approximately moving along the equator. However, it will also move north and south between the tropics over the course of a year, so it is spiraling like a helix. The subsolar point contacts the Tropic of Cancer on the June solstice and the Tropic of Capricorn on the December solstice. The subsolar point crosses the Equator on the March and September equinoxes. Coordinates of the subsolar point The subsolar point moves constantly on the surface of the Earth, but for any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wreath Of Analemmas
A wreath () is an assortment of flowers, Leaf, leaves, fruits, twigs, or various materials that is constructed to form a circle . In English-speaking countries, wreaths are used typically as household ornaments, most commonly as an Christmas decoration, Advent and Christmas decoration. They are also used in ceremonial events in many cultures around the globe. They can be worn as a Chaplet (headgear), chaplet around the head, or as a garland around the neck. Etymology The word ''wreath'' comes from Middle English ''wrethe'' and from Old English ''writha'' 'band'. History Ancient Etruscan wreaths Wreaths were a design used in ancient times in southern Europe. The most well-known are pieces of Etruscan civilization jewelry, made of gold or other precious metals. Symbols from Greek myths often appear in the designs, embossed in precious metal at the ends of the wreath. Ancient Roman writers referred to Etruscan ''corona sutilis'', which were wreaths with their leaves s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or ''parallels'', run east–west as circles parallel to the equator. Latitude and ''longitude'' are used together as a coordinate pair to specify a location on the surface of the Earth. On its own, the term "latitude" normally refers to the ''geodetic latitude'' as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or ''normal'') to the ellipsoidal surface from the point, and the plane of the equator. Background Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean sea level over the ocean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position Of The Sun
The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth's surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic. Earth's rotation about its axis causes diurnal motion, so that the Sun appears to move across the sky in a Sun path that depends on the observer's geographic latitude. The time when the Sun transits the observer's meridian depends on the geographic longitude. To find the Sun's position for a given location at a given time, one may therefore proceed in three steps as follows: # calculate the Sun's position in the ecliptic coordinate system, # convert to the equatorial coordinate system, and # convert to the horizontal coordinate system, for the observer's local time and location. This is the coordinate system normally used to calculate the position of the Sun in terms of solar zen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solar Time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Two types of solar time are apparent solar time (sundial time) and mean solar time (clock time). Introduction A tall pole vertically fixed in the ground casts a shadow on any sunny day. At one moment during the day, the shadow will point exactly north or south (or disappear when and if the Sun moves directly overhead). That instant is local apparent noon, or 12:00 local apparent time. About 24 hours later the shadow will again point north–south, the Sun seeming to have covered a 360-degree arc around Earth's axis. When the Sun has covered exactly 15 degrees (1/24 of a circle, both angles being measured in a plane perpendicular to Earth's axis), local apparent time is 13:00 exactly; after 15 more degrees it will be 14:00 exactly. The problem is that in September the Sun takes less time (as me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hour Angle
In astronomy and celestial navigation, the hour angle is the angle between two planes: one containing Earth's axis and the zenith (the '' meridian plane''), and the other containing Earth's axis and a given point of interest (the ''hour circle''). It may be given in degrees, time, or rotations depending on the application. The angle may be expressed as negative east of the meridian plane and positive west of the meridian plane, or as positive westward from 0° to 360°. The angle may be measured in degrees or in time, with 24h = 360° exactly. In celestial navigation, the convention is to measure in degrees westward from the prime meridian (Greenwich hour angle, GHA), from the local meridian (local hour angle, LHA) or from the first point of Aries (sidereal hour angle, SHA). The hour angle is paired with the declination to fully specify the location of a point on the celestial sphere in the equatorial coordinate system. Relation with right ascension The local hour angle (LH ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
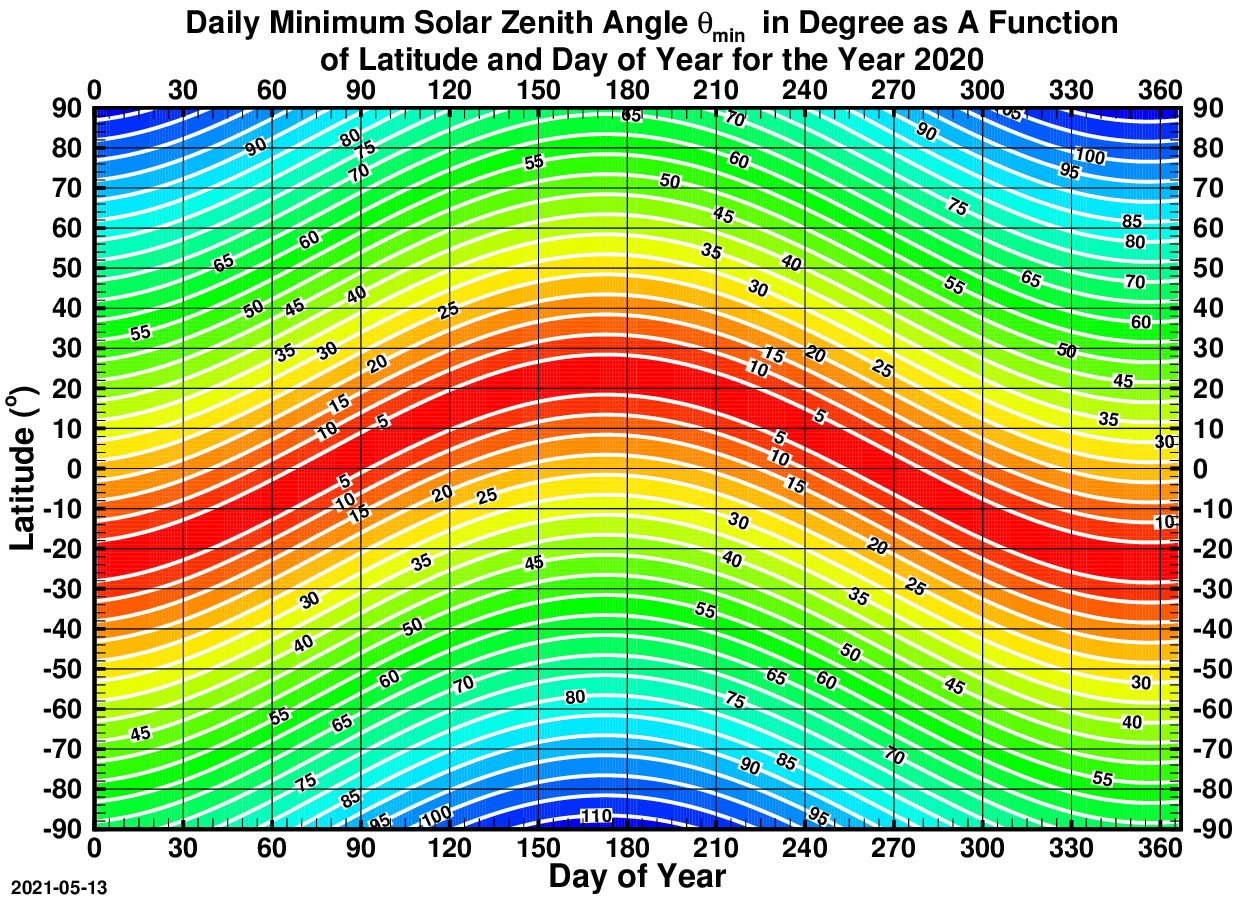
Solar Elevation Angle
The solar zenith angle is the zenith angle of the sun, i.e., the angle between the sun’s rays and the vertical direction. It is the complement to the solar altitude or solar elevation, which is the altitude angle or elevation angle between the sun’s rays and a horizontal plane. At solar noon, the zenith angle is at a minimum and is equal to latitude minus solar declination angle. This is the basis by which ancient mariners navigated the oceans. Solar zenith angle is normally used in combination with the solar azimuth angle to determine the position of the Sun as observed from a given location on the surface of the Earth. Formula : \cos \theta_s = \sin \alpha_s = \sin \Phi \sin \delta + \cos \Phi \cos \delta \cos h where * \theta_s is the ''solar zenith angle'' * \alpha_s is the ''solar altitude angle'', \alpha_s = 90° – \theta_s * h is the hour angle, in the local solar time. * \delta is the current declination of the Sun * \Phi is the local latitude. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Sine
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry. Notation Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: , , , etc. (This convention is used throughout this article.) This notation arises from the following geometric relationships: when measuring in radians, an angle of ''θ'' radians will correspond to an arc whose length is ''rθ'', where ''r'' is the radius of the circle. Thus in the unit cir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




%2C_Phang_Nga_Bay%2C_Thailand.jpg)